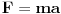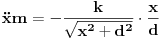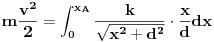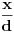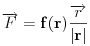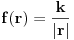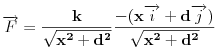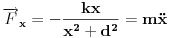[ Mooky @ 13.01.2016. 02:49 ] @
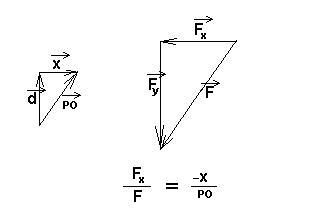
Molio bih nekog da mi pomogne pri rješavanju ovog problema.Prijedlog, riješenje, uputa, hint bilo kakva pomoc je dobrodošla.
Kako izraziti silu ili kako izgleda dif. jednačina kretanja. Očito je da neće biti kretanja duž Y-ose, y=d=const.
tako da ostaje aktivna komponenta sile paralelna sa x osom, tj. Fx=Fcos(phi) gdje je phi ugao između vektora r i x ose-
Intenzitet sile je dat kao F=k/|r| gdje je |r|=sqrt(x^2+d^2) a jedinicni vektor je (vektor r)/|r| što znači -(i*cos(phi)+j*sin(phi))/|r| Ukoliko ne grešim????
mx'' = ??????


[Ovu poruku je menjao Mooky dana 13.01.2016. u 03:59 GMT+1]
[ zzzz @ 14.01.2016. 10:33 ] @
Njutnov zakon kaže da promjenu brzine (ubrzanje) ostvaruje sila.Ubrzanje je drugi izvod puta po vremenu.Horizontalna komponenta Sile može se izraziti pomoću puta x.
Brzina se može izračunati rješavanjem diferencijalne jednačine,ali i iz kinetičke energije koja je jednaka radu sile na putu AC.





[ Mooky @ 15.01.2016. 20:14 ] @
Citat:
zzzz:
Njutnov zakon kaže da promjenu brzine (ubrzanje) ostvaruje sila.Ubrzanje je drugi izvod puta po vremenu.Horizontalna komponenta Sile može se izraziti pomoću puta x.
Brzina se može izračunati rješavanjem diferencijalne jednačine,ali i iz kinetičke energije koja je jednaka radu sile na putu AC.






Hvala na odgovoru, no ipak mi nije jasan faktor u izrazu za silu.Zar nije:
Opcenito:
Dato je da
Pa je:
Odakle dobijemo komponentu x:

Greška?

[Ovu poruku je menjao Mooky dana 15.01.2016. u 21:41 GMT+1]
[ zzzz @ 18.01.2016. 13:58 ] @
Citat:
Mooky: Hvala na odgovoru, no ipak mi nije jasan faktor u izrazu za silu.

Greška.
Treba da stoji PO umjesto d.To dolazi iz sličnosti dva vektorska trokuta.Iz omjera modula vektora sila i vektora duži nađemo modul horizontalne sile. Tvoj izraz za silu je principijelno pogrešan.Množiš modul sile sa jediničnim vektorom dužine.Takav umnožak može dati samo neki vektor puta a ne silu.U ovako koncipiranom zadatku to daje dobar rezultat,ali to neće biti u nekom drugom slučaju.