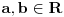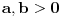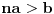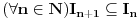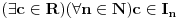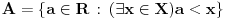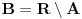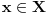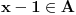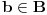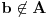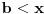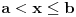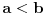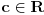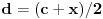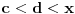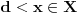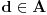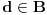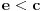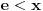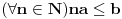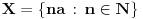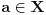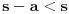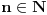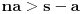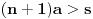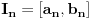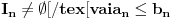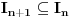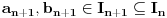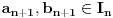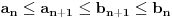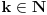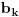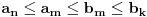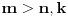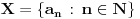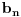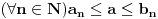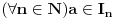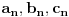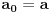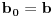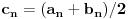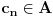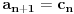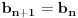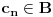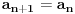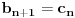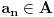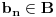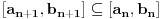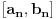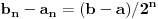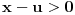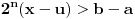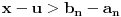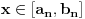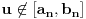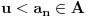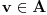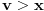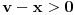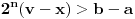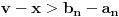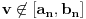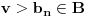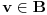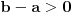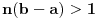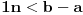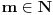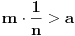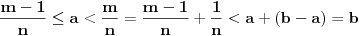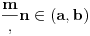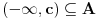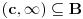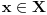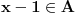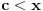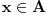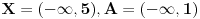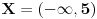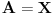To zavisi od toga šta izabereš za aksiomu (ili aksiome) neprekidnosti.
Aksioma supremuma (S): Svaki neprazan odozgo ograničen podskup od

ima supremum u

.
Dedekindova aksioma (D): Ako je skup

disjunktna unija nepraznih skupova

i

, pri čemu je svaki element skupa

manji od svakog elementa skupa

, onda postoji realan broj

takav da su svi realni brojevi manji od

članovi skupa

, a svi realni brojevi veći od

članovi skupa

.
Arhimedova aksioma (A): Za ma koje
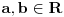
,
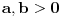
postoji

takav da je
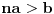
.
Kantorova aksioma (K): Ma koji beskonačan niz

nepraznih ograničenih zatvorenih intervala takav da je
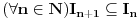
ima neprazan presek, odnosno
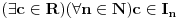
.
Važi da je (S) ekvivalentno sa (D), odnosno sa konjunkcijom (A) i (K).
(D) povlači (S):
Neka je

odozgo ograničen podskup od

i neka je
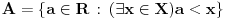
,
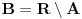
.
Pošto za
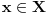
važi
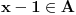
i ma koja majoranta skupa

pripada skupu

, skupovi

i

su neprazni. Očiglednosu disjunktni i unije im je

. Ako

i
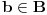
, onda postoji
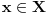
takav da je

. Zbog
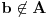
ne može biti
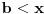
, pa je
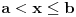
odnosno
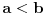
. Neka je
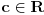
kao iz (D). Neka

nije majoranta od

i neka je
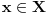
takvo da je

. Onda za
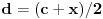
važi
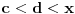
. Zbog
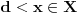
važi
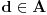
, a zbog

važi
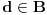
. Ta kontradikcija dokazuje da je

majoranta od

. Ukoliko bi neko
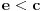
bilo majoranta, postojalo bi
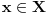
takvo da je
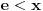
suprotno tome da je

majoranta od

. Stoga je

supremum skupa

.
S povlači D:
Ako važi S i A i B su skupovi kao u D, onda je skup A neprazan i odozgo ograničen, pa ima supremum c. Obzirom da je c majoranta od A, veći elementi od c ne mogu pripadati skupu A, pa pripadaju skupu B. Ako bi neki realan broj manji od c pripadao skupu B, onda bi i on bio majoranta skupa A, pa c ne bi bila najmanja majoranta (supremum). Prema tome, realni brojevi manji od c ne mogu pripdatai skupu B, pa pripadaju skupu A.
D povlači A:
Neka važi D i ne važi A. Neka su a i b takvi pozitivni realni brojevi da za sve prirodne brojeve n važi da je na manje ili jednako od b. Neka je A skup svih realnih brojeva x takvih da je x<na za bar jedan prirodan broj n i neka je B komplement skupa A. Pošto b ne pripada skupu A, b pripada skupu B. Takođe, a pripdada skupu A jer je a manje od 2a. Skup R je disjunktna unija nepraznih skupova A i B. Neka je x element skupa A i y element skupa B. Neka je n prirodan broj takav da je x<na, što je manje ili jednako od y, važi x<y. Neka je c razdva
(S) povlači (A):
Neka važi (S) i ne važi (A). Neka su
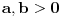
takvi da
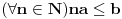
. Skup
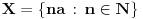
.
Skup

je neprazan zbog
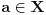
a odozgo ograničen jer mu je

majoranta. Stoga ima supremum

. Zbog
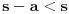
broj

nije majoranta skupa

pa postoji
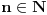
takvo da je
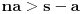
, odnosno
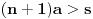
, što je u suprotnosti sa tim da je

supremum skupa

.
(S) povlači (K):
Neka je

inkluzijski nerastući niz nepraznih ograničenih zatvorenih intervala i neka je
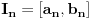
. Zbog
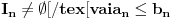
. Zbog
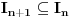
i
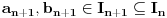
važi
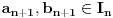
, odnosno
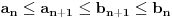
, pa je niz

neopadajući i za svako
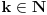
broj
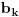
je majoranta niza

(jer je
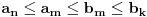
za ma koje
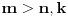
). Stoga je skup
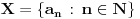
nepraznan i odozgo ograničen, pa ima supremum

, koji ne prelazi nijednu majorantu, pa ni
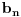
. Stoga je
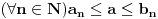
, odnosno
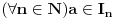
.
(A) i (K) povlači (D):
Neka su

i

kao u (D). Za

i
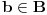
važi
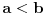
i konstruišimo nizove
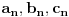
na sčedeći način:
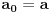
,
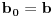
,
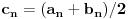
.
Ako je
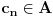
, onda je
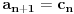
i
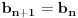
.
Ako je
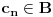
, onda je
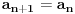
i
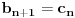
.
Niz

je neopadajući, a niz
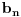
nerastući, pri čemu je
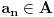
,
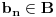
i
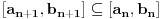
. Stoga postoji neko

koje pripada svakom od intervala
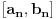
. Takođe je
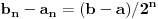
.
Neka je

. Pošto je
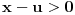
postoji
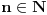
takvo da je
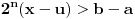
, pa je
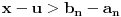
zbog čega ne mogu oba od brojeva

i

da pripadaju intervalu
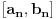
. Obzirom da
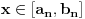
[/tex] zaključujemo da
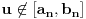
, pa zbog

važi
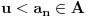
, odakle sledi
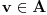
.
Neka je
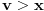
. Pošto je
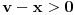
postoji
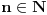
takvo da je
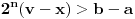
, pa je
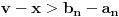
zbog čega ne mogu oba od brojeva

i

da pripadaju intervalu
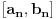
. Obzirom da
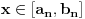
[/tex] zaključujemo da
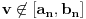
, pa zbog
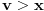
važi
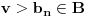
, odakle sledi
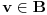
.
Gustina skupa

u

je posledica od (A).
Neka je
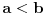
. Zbog
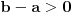
postoji

takvo da je
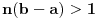
, pa je
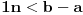
. Postoji
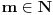
takvo da je
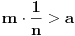
. Uočimo najmanje takvo celobrojno

. Dakle,
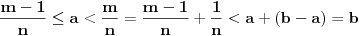
, pa
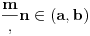
.