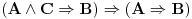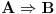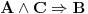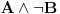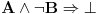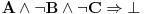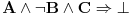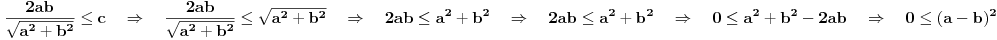|
|
[ miki069 @ 02.10.2020. 10:56 ] @
|
| Radi se o 30-tom zadatku sa Kengura 2010 za 11-12 razred.
Da li ima neko korektno rešenje?
Pretpostavka da je PQ paralelno sa AB se ne(sme) uvesti?
Zadatak i neko rešenje su u prilogu.
[Ovu poruku je menjao miki069 dana 02.10.2020. u 13:18 GMT+1] |
[ djoka_l @ 02.10.2020. 13:09 ] @
Ja sam radio slišno kao ti.
Nisam koristio sinuse uglova nego činjenicu da se dobiju slični trouglovi, pa sam odnose stranica stavio u zbir.
Druga razlika, ono što si ti nazvao x, meni je bilo a-x, a ono što si ti nazvao y, ja sam stavio b-y
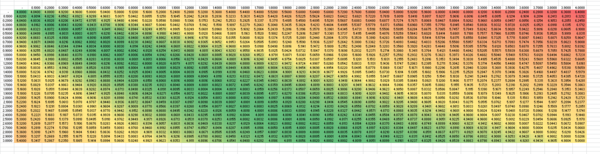
Na kraju sam dobio da je zbir stranica (2ab-bx-ay)/c +sqrt(x^2 + y^2)
Pošto mi se nisu radili izvodi, probao sam da stavim ekstremne vrednosti, pa sam našao da mi je minimalan rezultat 2ab/c, a to je i bio jedan od ponuđenih odgovora.
Za proveru sam napravio u Excelu tabelu sa trouglom koji ima katete 3 i 4 i varirao x i y u koracima po 0.1 i dobio isti rezultat...
 [ miki069 @ 02.10.2020. 18:47 ] @
Izvodi i ne pomazu jer suma nije diferencijabilna za X=0 i Y=0 (koristio sam tvoje resenje).
Pretpostavka o paralelnosti PQ sa AB daje ispravno resenje za problem minimuma, a pogresno za maksimum. Za problem maksimuma ne pomaze ni tvoja metodologija rubnih tacaka.
[ djoka_l @ 02.10.2020. 19:28 ] @
Za slučaj x=0 i y=0 dobijamo komponentu vrednosti izvoda 0/0 , pa iako je vrednost neodređena, može da se nađe vrednost primenom Lopitalove teoreme.
Međutim, obzirom na uzrast za koji je namenjen zadatak, nisam smatrao da je primenljivo da se radi parcijalna intregracija funkcije 2 promenljive. Čak mislim da se ni na fakultetima do druge ili treće godine ne rade takve stvari.
Ja sam rešenje proverio i na wolframu, s tim da sam uzeo "blaža" ograničenja, x<=4 i y<=3 za trougao koji ima katete 3 i 4, čisto da ne bih dobio previše opšte rešenje. Praktično rešenja sa negativnim vrednostima x i y nemaju smisla, ali sam ostavio da to reši wolfram.
https://www.wolframalpha.com/i...2%29+for+x%3C%3D4+and+y%3C%3D3
Wolfram nalazi da je vrednost x i y skup tačaka (ne obavezno nule), što sam video i u mom excelu
ono što kaže wolfram je da je minimum 2ab/c za sve tačke P i Q za koje važi da je y=ax/b [ miki069 @ 02.10.2020. 20:12 ] @
Zaboravimo uzrast. Lopitalovo pravilo ne pomaze kod funkcije dveju promenljivih. Ako bi resavali problem maksimuma iste sume, sta onda kazu Wolfram i Excel?
[ djoka_l @ 02.10.2020. 22:13 ] @
Excel kaže da je maksimum kada je Q na kraju duže katete, a P se poklapa sa tačkom C. Za wolfram nisam tražio rešenje za maksimalnu vrednost.
Ja sam do rešenja došao pre nego što sam proverio u excelu i wolframu, a pošto je pitanje bilo abcd pitalica, jedini logičan odgovor mi je bio onaj koji si i ti zaokružio. Čak nije bilo potrebno pokazati ni postupak, ja sam stao kada sam dobio izraz za zbir traženih duži, i jedino je tvoj odgovor imao smisla, a bez dublje analize...
Mislim da je ovo bio prilično težak zadatak, možda je postojala brža i jednostavnija verzija postupka, ali ja do nje nisam došao.
[ miki069 @ 03.10.2020. 05:28 ] @
Nisam ni ja. Mozda neko uspe.
[ peromalosutra @ 03.10.2020. 09:38 ] @
Mislim da je rjesenje a:b=ctg(15).
Na brzinu sam isjekao sliku pa telefonu pa se ne vidi najbolje. Uglavnom, oznaceni ugao je 15 stepeni, sto se lako pokazuje na osnovu datog ugla od 30 i cinjenice da je ugao dijagonale kvadrata 45. Nakon toga se samo pozove na trigonometriju.
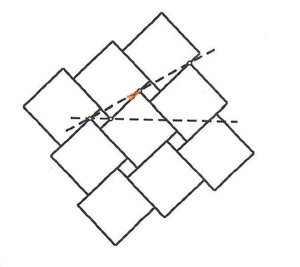
Dakle rjesenje je pod B: (2+sqrt(3)):1
Numericki je 2+sqrt(3) = ctg(15), e sad vjerovatno bi i to trebalo pokazati.
[Ovu poruku je menjao peromalosutra dana 03.10.2020. u 11:54 GMT+1][ miki069 @ 03.10.2020. 10:48 ] @
Pero ne treba 26-ti vec 30-ti zadatak.
[ peromalosutra @ 03.10.2020. 11:31 ] @
Uh, pardoniram :) Izgleda da nisam ni procitao pitanje kako treba.
[ Bojan Basic @ 03.10.2020. 11:57 ] @
Citat: miki069:
Pretpostavka da je PQ paralelno sa AB se ne(sme) uvesti?
Čini mi se da sledeće rešenje prolazi: zamislimo još i da je tačka Q fiksirana, i samo tačku P pomeramo po kateti BC; zanima nas kada se minimum dostiže za taj fiksirani položaj tačke Q. Ispostavlja se da se minimum dostiže kad su trouglovi ABC i PQC slični, i to baš u ovom redosledu temena (nadam se da nisam zeznuo račun: prosto možemo posmatrati prvi izvod one funkcije koju miki069 ima na prvoj strani, ali to posmatramo kao funkciju jedne promenljive, samo po x, sve ostalo su konstante; verovatno može i nekim kreativnijim argumentom pošto zaključak ima lepu geometrijsku interpretaciju, ali svakako je i ovo skroz pravolinijski). Dakle, odatle zaključujemo da ne možemo baš uvesti ovu pretpostavku koju sam citirao gore, ali možemo malo drugačiju, njoj srodnu (posmatramo samo položaje prave PQ koji odsecaju trougao PQC sličan trouglu ABC, ali, napominjem, baš u ovom redosledu temena, to je tačno obratan redosled od onog koji bismo imali kada bi PQ i AB bile paralelne). Pa sad kad imamo tako restrikovan položaj prave PQ, odatle nije teško dovršiti.
Ovo sve gore je bilo za računanje minimuma. Ako nas zanima maksimum, onda je čak malo jednostavnije: isti argument (fiksiramo jednu tačku pa mrdamo samo drugu) vodi do zaključka da jedna tačka mora biti baš u temenu, i onda je praktično trivijalno. [ miki069 @ 04.10.2020. 12:20 ] @
Hvala Bojane.
[ Nedeljko @ 04.10.2020. 16:06 ] @
Samo da razjasnim šta znači da se nešto može pretpostaviti bez umanjenja opštosti.
Recimo da imamo neke aktuelne pretpostavke A i da treba da izvedemo neki zaključak B. Iskaz da bez umanjenja opštosti možemo pretpostaviti C znači da važi
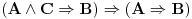 .
Drugim rečima, to znači da željeni stav 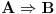 možemo izvesti kao posledicu stava 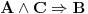 . [ miki069 @ 04.10.2020. 21:41 ] @
Ako je C netacan iskaz? Navedena implikaciia nije tautologija? Jasno je da A tacan iskaz. Problem je iskaz B.
[ Nedeljko @ 04.10.2020. 22:25 ] @
A i B imaju nepoznate istinitosne vrednosti i treba dokazati da je isključeno da je A tačan, a B netačan.
Za to je dovoljno dokazati da je isključeno da je A tačan, a B i C netačni (to znači da se C može pretpostaviti bez umanjenja opštosti) i da je isključeno da su A i C tačni, a B netačan (što znači da B sledi iz A i C).
To znači da je isključena mogućnost da je A tačno, a B netačno, bez obzira da li je C tačno ili netačno.
Ima ovo opštiju formulaciju, ali za početak ovako.
[ miki069 @ 04.10.2020. 23:02 ] @
A je tačan jer je to pretpostavka zadatka.
Ako bi C bio netačan, formula je tačna i ako je tvrđenje B netačno.
[Ovu poruku je menjao miki069 dana 05.10.2020. u 06:55 GMT+1]
[ Nedeljko @ 05.10.2020. 08:34 ] @
Zadatak je dokazati da 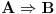 .
Dakle, treba izvesti protivrečnost iz 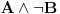 , odnosno dokazati da 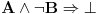 .
To možeš učiniti diskusijom po  , odnosno tako što dokažeš da 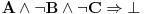 (odnosno da se  može pretpostaviti bez umanjenja opštosti) i 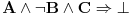 (odnosno da tvrđenje važi uz dodatnu pretpostavku  ). [ mjanjic @ 05.10.2020. 20:51 ] @
Bojan je dao dobru ideju, mislim da važi činjenica da je npr. PQ + HQ minimalno kada su PCQ i AHQ slični.
Sećam se prošlogodišnjeg zadatka sa primenom na ETF-u, nešto tipa iz tačke (2,3) i (3,5) se povuku duži do tačke M između 2 i 3 na x-osi, naći položaj tačke M tako da zbir duži iz date 2 tačke do tačke M bude minimalna - rešenje je takvo da te duži sa visinama iz datih tačaka na x-osu i delovima x-ose grade slične trouglove - to je problem konopca vezanog krajevima za vrhove stubova različite visine koji dodiruje tlo, minimalna dužina se dobija u tački koja je teme sličnih trouglova (stubovi, linije na tlu od tačke dodira konpoca sa tlom i stubova, i samog konopca).
Nisam imao vremena da proveravam dokaz ovoga, ali su i ovi na ETF-u valjda računali na poznavanje tog problema, pa se dati zadatak onda rešava brzo. Ako se krene sa izvodima i sl., brzo se pogubi u računu, i mislim da se to rešava pomoću nejednakosti, gde je granični slučaj jednakost, ali sam zaboravio koju nejednakost treba primeniti.
Dakle, rešenje bi trebalo da bude da je trougao PCQ bude sličan trouglu ABC.
Međutim, to važi kada jedna od tačaka P i Q fiksirana.
Problem je što, ako zadržimo princip, a pomeramo obe tačke P i Q, dobijamo praktično da je P = Q = C, a K = H, čime se u stvari i dobija ekstrem za funkciju koju je odredio miki (ispod nacrtanog trougla, na strani 2, zaokruženo rešenje u zadatku dobija se za x=a, y=b, samo pošto je c nepoznato, u rešenju su umesto c napisali koren iz a^2+b^2).
Da li je minimum slučaj kada je P=Q=C ili kada je Q=A, može lako da se proveri, pa ću preći na sledeći slučaj.
Drugi slučaj, kada je trougao PCQ kao lik u ogledalu u odnosu na prethodni slučaj trougla PCQ, ima dva ekstrema - ono koje je već prethodno dobijeno, i drugo za koje važi P=B=K, Q=A=H. U tom slučaju, zbir datih duži je jednak c, pa treba proveriti da li je to veće ili manje od prethodno dobijenog rešenja.
Dakle, pretpostavimo da je prvo dobijeno rešenje minimum, tada je:
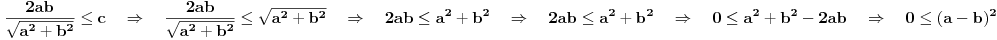
što je uvek tačno! [ Časlav Ilić @ 06.10.2020. 13:20 ] @
Nešto ne vidim potrebu za specijalnim zaključivanjem ako sme da se koristi znanje uslova da izvod sume po oba parametra, npr. kao x i y koje je uveo Miki, mora da bude nula u ekstremumu. To što funkcija nije diferencijabilna za neke vrednosti parametera može, ali ne mora da bude bitno, u zavisnosti od položaja ekstremuma. Ja sam (čisto slučajno, svejedno je) uveo obrnute parametre od Mikija, takve da mere od temena pravog ugla do tačaka P i Q, nazovimo ih a' i b'. Kad se sa njima sastavi tražena suma i njeni izvodi po a' i b' izjednače sa nulom, dobije se da je rešenje svako a' i b' za koje važi a'/b' = b/a (tj. dobije se u prethodnom porukama već pomenuta sličnost odgovarajućih trouglova); uz prirodna ograničenja 0 <= a' <= a i 0 < b' <= b. Onda izaberem npr. a' = 1/a i b' = 1/b, ubacim u sumu, i dobijem rešenje pod V. (Da je ovaj ekstremum zapravo minimum a ne maksimum, ne treba dokazivati ako se veruje postavci zadatka.)
[ mjanjic @ 06.10.2020. 20:36 ] @
Ponuđena rešenja mogu da budu takva izvedeš pogrešan zaključak ako sve ne proveriš. Ovde to možda nije potrebno, ali da nismo znali koje je rešenje tačno, pitanje je kako bismo došli do tačnog rešenja i da li bismo bili sigurni da je to zaista tačno rešenje.
[ miki069 @ 08.10.2020. 09:34 ] @
Časlave funkcija nije diferencijabilna baš u tački minimuma. Slažem se da diferencijabilnost nije uslov za minimum.
Iz izjednačavanja parcijalnih izvoda sa nulom dobija se isti uslov koji je Bojan izveo geometrijski, gde je ključna sličnost trouglova PQC i ABC.
Tvoj račun je dosta pojednostavljen, jer iz činjenice da je a'/b' = b/a ne mora da sledi a' = 1/a i b' = 1/b, već samo da je a' = b'*(b/a).
Obrnuto važi.
Detaljan račun je u prilogu.
Bitno je da pretpostavka da je PQ paralelan sa AB je geometrijski neispravna, već da je tačno da je trougao PQC sličan sa ABC.
Iz analize ni limesi ne pomažu u ovom zadatku jer u tački minimuma parcijalni izvodi teže u beskonačnost.
Interesantno je dai spada da funkcija i ne zavisi od X, već se direktno dobija minimum.
Janjiću oćemo zadatak sa konopcem u ovoj temi ili posebnoj?
Ali težu verziju gde konopac ne dodirne tlo.
Taj zadatak je bio na republičkom takmičenju u Novom Sadu 1996. godine za I godinu srednje škole.
Možda je Bojan i bio na tom takmičenju.
[ miki069 @ 08.10.2020. 14:53 ] @
Za vrhove dva stuba visine 11 i 15 metara koji su na rastojanju od 9 metara zakacen je kanap duzine 15 metara. Na kanap je okacen teg i pusten da klizi, sve dok se ne nadje u najnizoj tacki. Na kojoj visini ce se tada nalaziti teg?
[ MajorFatal @ 08.10.2020. 17:06 ] @
Na visini od preko 5 metara :)
[ miki069 @ 08.10.2020. 19:18 ] @
Jeste majore preko 5 metara. Tacno je 7 metara. Opet nedostaje tacna geometrijska interpretacija.
[ mjanjic @ 08.10.2020. 22:42 ] @
Svejedno je da li dodiruje tlo ili ne, jer za istu dužinu konopca važna je samo razlika u visini stubova, sve dok je konopac iznad tla ili samo jednom tačkom dodiruje tlo.
[ miki069 @ 10.10.2020. 11:33 ] @
Logicko-geometrijski su u pravu. Ali je racunski mnogo tezi zadatak kada je h>0. Kada je h=0 imamo dve nepoznate. Inace je 5 nepoznatih i vise ima da se racuna.
[ MajorFatal @ 10.10.2020. 23:51 ] @
Citat: miki069:
Jeste majore preko 5 metara. Tacno je 7 metara. Opet nedostaje tacna geometrijska interpretacija.
Nisam pri kompu pa ne mogu da crtam, ali meni bi pomoglo ako bih docrtao još jedan imaginarni stub od 11 metara, bliže stubu od 15 metara, ali tako da dodiruje već zategnut kanap u svojoj najvišoj tački. Kanap bi između 2 stuba od 11 metara morao u odnosu na simetralu koja prolazi kroz teg da zauzima simetričnu trasu, a iznad imaginarnog stuba od 11 m da se nastavlja po istom pravcu do vrha stuba od 15 m.
Pa bi se računica svela na 11 - 4 = 7 :) bez ikakvih h..
[ miki069 @ 11.10.2020. 09:00 ] @
Levi trougao i donji desni su ti podudarni. Gornji desni je samo slican sa ta dva trougla. Nemas garanciju da je podudaran. U ovom primeru slucajno dobijas ispravno resenje. U opstem slucaju ne. Resenje je u prilogu.
[Ovu poruku je menjao miki069 dana 11.10.2020. u 11:36 GMT+1]
[ MajorFatal @ 11.10.2020. 10:05 ] @
Pa dobro, pošto nisam rešio, nemam pravo da postavljam sledeći zadatak, pa ćeš morati ti :)
[ miki069 @ 11.10.2020. 11:33 ] @
Ako bi uzeli da je rastojanje izmedju stubova 12metara onda bi a ispalo 5/2, a to je razlicito od 4. Nije ovaj zadatak zavrsen. Nedostaje dokaz da je trougao APM slican sa BQM.
[ MajorFatal @ 11.10.2020. 13:13 ] @
Za dokaz te sličnosti možda možeš da docrtaš novi imaginarni stub visine 15 metara levo od stuba od 11 m, a čiji bi se vrh poklapao sa pravcem kao kad produžiš kanap iz tačke A, APM mora da bude sličan sa novonastalim trouglom kad bi produžio QP, a ovaj je identičan sa BQM?
[ miki069 @ 11.10.2020. 13:47 ] @
U resenju pise da ako bi produzili duz BM do preseka sa levim stubom (neka to bude tacka F) da tacka M (ravnotezni polozaj tega) mora da lezi na simetrali duzi AF. Posle ide neko objasnjenje da ako ne bila na toj simetrali da ne bi AM + MB bilo 15 metara. To objasnjenje je dosta klimavo.
[ MajorFatal @ 12.10.2020. 12:01 ] @
Pa to jeste tako verovatno, nego koliko je ovo zadatak iz matematike a koliko iz fizike?
[ miki069 @ 12.10.2020. 15:38 ] @
Bio je na republickom takmicenju iz Matematike. Da je data masa tega i jos ponesta onda bi bio iz Fizike. Meni jos uvek nije jasno sto su slicni trouglovi.
[ MajorFatal @ 12.10.2020. 17:31 ] @
Nije data masa tega ali ja moram da pretpostavljam kako se ponaša konopac na koji je okačen teg u "najnižoj" tački.
Docrtaj stub od 15m i produži kanap iz A i liniju QP do njega, mislim da je očigledno.
[ miki069 @ 13.10.2020. 19:07 ] @
U Geometriji ne postoji "ocigledno".
[ MajorFatal @ 14.10.2020. 08:28 ] @
U geometriji ne postoje ni stubovi, kanapi, tegovi.. nego samo tačke, prave, kružnice.. :)
Pa evo, novi stub od 15m bi bio paralelan :) sa starim stubom od 11m jer su oba normalno pobodeni u zemlju, a QP kad se produži bi bila normala na njega, a kanap kad se produži iz A bi stigao do vrha tog stuba, i onda zbog paralelnosti stuba i AP, i zbog zajedničkih pravi PQ i MA bili bi slični BQM i APM eto.
[ miki069 @ 14.10.2020. 15:48 ] @
Ukapirao sam. Hvala majore.
[ MajorFatal @ 14.10.2020. 16:27 ] @
Ma nema na čem, ti izvini što ovako nakaradno "ilustrujem" ali nisam pri kompu..
[ mjanjic @ 14.10.2020. 22:57 ] @
Davno, kad sam bio na republičkom iz fizike, zadatak bio da se nađe period oscilovanja klatna (teg okačen o kanap dužine L) u zavisnosti od dužine kanapa L - nigde nije data masa, doduše od nje i ne zavisi, ako se radi o matematičkom klatnu (zanemareno trenje vazduha i drugi gubici). To učenici iz klasičnih gimanzija ne mogu da urade, mogu samo ovi što idu u Prirodno-matematičku, jer tamo uče već u 1. godini matematiku koja je potrebna da se reši matematičko klatno.
[ MajorFatal @ 23.10.2020. 17:17 ] @
Malopre video, a možda nekom bude zanimljivo jer je sličan sa prethodnim sa stubovima i kanapom.. navodno na prijemnom za Amazon..
Kabal (kabl, uže) dužine 80 metara, razapet je između dva stuba od po 50 metara, tj. visi slobodno između vrhova dva stuba, i dolazi do visine od 20 metara iznad zemlje u svojoj najnižoj tački. Koliki je razmak između ta dva stuba od po 50 metara visine, između čijih vrhova je razapet kabl? Posle toga treba rešiti ako najniža tačka kabla doseže do 10 metara iznad zemlje. Navodno nisu potrebna znanja iz fizike...
[ Bradzorf012 @ 03.01.2021. 18:37 ] @
Ako sam pogrešio, nadam se da će neko ispraviti.
[ miki069 @ 04.01.2021. 10:46 ] @
Sve je dobro do procene minimuma. Za x i y su oba nula je trivijalno. Jednakost vazi i za a*x = b*y. A to je netrivijalan slucaj. Bojan ga je genijalno objasnio geometrijski, a ja finisirao racunski. Bitan je bio geometrijski pristup problemu minimuma. Racunski je sve jasno.
[Ovu poruku je menjao miki069 dana 04.01.2021. u 12:02 GMT+1]
[ B3R1 @ 04.01.2021. 11:27 ] @
Citat: MajorFatal:
Malopre video, a možda nekom bude zanimljivo jer je sličan sa prethodnim sa stubovima i kanapom.. navodno na prijemnom za Amazon..
Kabal (kabl, uže) dužine 80 metara, razapet je između dva stuba od po 50 metara, tj. visi slobodno između vrhova dva stuba, i dolazi do visine od 20 metara iznad zemlje u svojoj najnižoj tački. Koliki je razmak između ta dva stuba od po 50 metara visine, između čijih vrhova je razapet kabl? Posle toga treba rešiti ako najniža tačka kabla doseže do 10 metara iznad zemlje. Navodno nisu potrebna znanja iz fizike...
To i nije klasican zadatak, vec vise filter za strebere, u stilu naseg starog pitanja o reci koja protice ispod Savskog mosta. To pitanje je obicno za pozicije u prodaji i marketingu, gde se ne ocekuje neko briljantno znanje algoritama i matematike, vec vise snalazljivost i "out of the box" razmisljanje. To pitanje recimo ne postavljaju programerima i network inzenjerima, jer je tu znanje bitnije od snalazljivosti, dok je kod trgovaca i marketara situacija bas obrnuta.
Zadatak ima nekoliko varijanti, a u ovoj koju si pomenuo najniza tacka tog kanapa je 10 metara od zemlje, duzina kanapa 80 metara a stubici su visine 50 metara. Ponekad promene malo cifre - recimo kazu da je duzina kanapa 60 metara, a najniza tacka 20 metara (stubici su opet po 50 metara). Trik je u tome da zamislis da je jedan kraj tog kanapa otkacen, a potom zakacen za isti stubic na kome je pricvrscen drugi kraj kanapa i da "izmeris" koliko je kanap udaljen od zemlje u tom slucaju. Onda dolazis do resenja u jednom potezu.
Naravno, kada se na intervjuu pojavi neki streber, on odmah krene da crta Dekartov koordinatni sistem, pa obelezi ose x i y, pa krene da izvodi razne jednacine, neki u to ubace i neke egzoticne metricke prostore i upetljaju se u problem kao pile u kucine ... [ Bradzorf012 @ 04.01.2021. 13:12 ] @
Miki
Da, nisam naveo da se minimum dostiže i za ax = by, ali ne vidim poentu "trivijalnosti". U zadatku se ne traži da se odrede lokalni ekstremi neke funkcije, već nešto sasvim drugo. Ok, to "drugo" jesu ekstremi, ali zadatak je srednjoškolski, pa samim tim nema govora o primeni parcijalnih izvoda i slično.
[ miki069 @ 04.01.2021. 19:47 ] @
Nikakvi izvodi nisu ni korisceni u resenju zadatka. Pogledaj resenje. Kljucan je uslov minimuma. Pogledaj obnasnjenje koje je dao Bojan Basic. Ovo tvoje je lepo izvedeno. Dobra je ocenjena nejednakost i iz nje sleduje da jednakost vazi za a*x = b*y. Tako da ovo tvoje upravo dokazuje slicnost koju je Bojan objasnio geometrijski. Meni je jasniji ovaj tvoj racunski pristup. Ali moras da predjes iz veze samo na x i jos par koraka racuna. Nekorektno je racunski odmah da su x i y = 0. Lepse si slozio sumu nego ja. Da sam ih slozio kao ti, ja temu ne bih ni otvarao. Mislim da je sve OK. Pozdrav.
[ Bradzorf012 @ 04.01.2021. 20:00 ] @
Ništa sporno.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|