Pretpostavljam da je ovo potrebno da se reši bez digitrona.

Koristi se osobina modulo funkcije.
Ako treba da se nađe poslednja cifra, tada treba naći mod10 proizvoda.

Modulo funkcija (bilo koja, ne samo ostatak pri deljenju sa 10) ima sledeću osobinu:
mod10(a*b) = mod10( mod10(a)*mod10(b) )
mod10(a+b) = mod10( mod10(a)+mod10(b) )

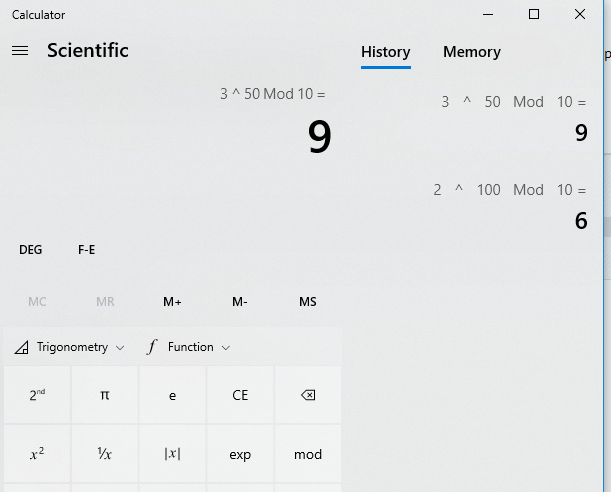
Već si našao da je mod10(2⁵) = 2 i mod10(3⁵)=3

Kako je 100=5*5*4 to je mod10(2¹⁰⁰)=mod10(2⁴) = 6 (one petice daju 2)
50=5*5*2 pa je mod10(3⁵⁰) = mod10(3²)=9

Onda je krajni rezultat mod10(6*9) = 4

Da, potrebno je resiti bez digitrona i rastavljanjem uproscavanjem stepena i izlozilaca....te onda dobiti rezultat

OK, da li ti je jasan postupak koji sam ti opisao?

Da, i hvala puno. Probacu sada da odradim jos neki primer. Hvala!

Evo ti primer, koji nije tako prost, ali se koristi osobina modulo funkcije.
Nađi mod(1000,97)
Uopšte nije važno kako ćeš predstaviti (rastaviti) broj 1000, bitno je da ga rastaviš na proizvod/zbir brojeva za koje ti je lako da nađeš mod 97

Ako postavljaču teme nije jasno, pravilo množenja se u ovom slučaju višestrukog eksponenta svodi na (ovde LaTeX ne prihvata \mod, pa sam koristio \pmod{N} koji dodaje zagrade oko "mod N"):




Nadam se da ovo nije bilo potrebno, ali čisto da postavljač teme shvati da se ne razlaže na , što je greška koju neki osnovci često naprave ako nisu vežbali ove zadatke.
Korak gde se modul primenjuje na izraz 2^5 je ispravnije uraditi prvo za izraz (2^5)^5 koji se stepenuje na 4, pa tek onda za 2^5, ali je rezultat isti, pa je jasnije kako je napisano.

Rekao bih da se funkcije mod i int ne uče u osnovnoj školi.Ako je tako onda bi osnovci mogli zaključivati ovako:
-Zadnja cifra potenciranja baze 2 se ciklički ponavlja 2,4,8,6,2,4,8,6....Ako je četvrta šestica onda je i četrdeseta,osamdeseta,devedeset šesta pa i stota je 6.
-Za bazu 3 ide 3,9,7,1,3,9,.....Ako je četvrta jedinica onda je i četrdeset osma jedinica.Četrdeset deveta je 3,a pedeseta je dakle 9.
umnožak zadnjih cifara je 6*9=54 odakle je rješenje zadatka broj 4.

Nema potrebe da rastavljas. Na dobrom si putu. Ako je interval 4, vidi koja je cefra na poslednjem mestu 2⁴ i ta ce biti i na poslednjem mestu od 2¹⁰⁰ (jer je 100 deljivo sa 4). Isti princip i za drugi broj. I, kao sto si rekao: pomnozis i vidis koja je poslednja cifra.
Ono sto je djoka_l pisao je, koliko sam na brzinu preleteo, formalniji zapis iste stvari.