[ zzzz @ 16.03.2024. 23:05 ] @
Naći preostale uglove pravouglog trokuta ako mu je površina S=2 i hipotenuza a=4.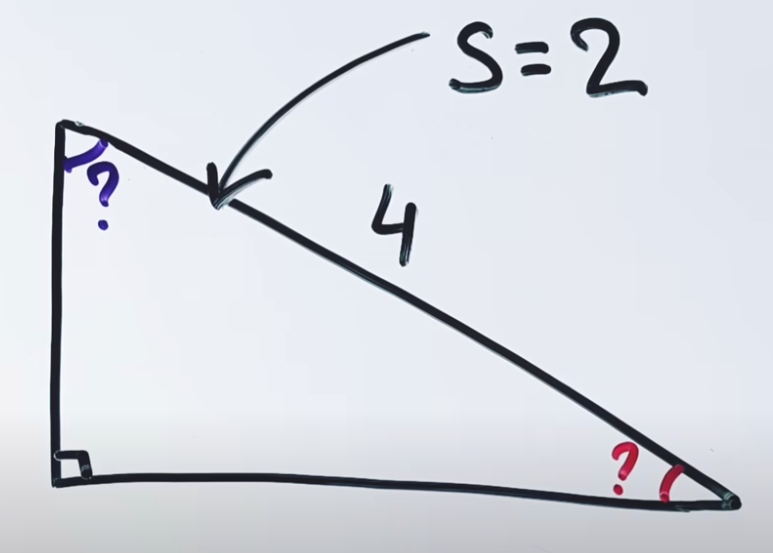 |
|
[ zzzz @ 16.03.2024. 23:05 ] @
[ B3R1 @ 17.03.2024. 10:21 ] @
Pitanje nije kako resiti zadatak, vecina forumasa ce ti dati rezultat relativno brzo. Pitagora + kalkulator, par puta arccos() i arcsin() i dobijes uglove od 75 i 15 stepeni.
Ali secajuci se srpskog sadomazohistickog skolstva, cisto sumnjam da ce ljudi iz skupa { ucitelji(ce)*, nastavnic[ie], profesori(ce)* } priznati takvo resenje ... a velika je verovatnoca da ce reci: zabranjeni su kalkulatori na pismenom / kontorlnom / ispitu ... Tako da se ovde verovatno trazi cinculiranje s trigonometrijom, u smislu formula za polovinu ugla, dvostruki ugao i tako to. Uglavnom, ako oznacis hipotenuzu sa c, pocinjes od dve jednacine koje su ocigledne: 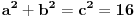 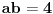 Ako je ab = 4, tada je 2ab = 8, pa hiphop kombinacijama prvu jednacinu mozes da prikazes kao kvadrat zbira ili kvadrat razlike i da od toga formiras 2 jednacine: 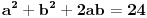 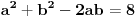 odatle dobijas: 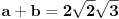 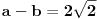 Sada ovo gore saberes i dobijas rezultat za stranice a i b: 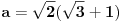 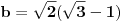 E sad, tu se verovatno dale treba cimati s onim silnim trigonomentrijskim formulama za dvostruke uglove i polovine ugla, jer je sqrt(3) kosinus ugla od 30 stepeni ... pa raznim trange-frange operacijama dodjes do rezultata. E, mene mrzi da se dalje patim s tim ... P. S. U eri gde AI preti da zameni gomilu poslova maltretirati decu ovakvim stvarima je besmisleno. Pogotovo je besmisleno i to ako im ne das te trigonometrijske formule da koriste za vreme ispita, vec im das samo papir i olovku, a ako ih uhvatis s puskicama obaras ih ... i tako ih pretvaras u bubalice besmislenih stvari, koje ce ionako zaboraviti cim dobiju diplomu. Nikakvo cudo sto Srbija ima najgore rezultate na PISA testovima. Zemlja bubalica! [ scoolptor @ 17.03.2024. 10:29 ] @
Citat: U eri gde AI preti da zameni gomilu poslova maltretirati decu ovakvim stvarima je besmisleno. Cilj je da se nauci proces resavanja problema, a ne pamcenje podataka i formula. Stoga ovo nije maltretiranje. Za celu trigonometriju je potrebno da znas 4 osnovne formule, i da si snalazljiv. [ B3R1 @ 17.03.2024. 12:07 ] @
Citat: scoolptor: Cilj je da se nauci proces resavanja problema, a ne pamcenje podataka i formula. Da. Ali koliko dece to shvati sta im je cilj tokom skolovanja? 0.0000001%? Svi ostali bubace ... i ponavljaju kako je cilj teme da im prodje vreme - dok ne stignu kuci i ne uhvate se neke zabave, sta god ta zabava bila. Sto se tice resavanja - bolje je dati im list sa svim formulama, taj koji kapira ce resiti problem brze ... a taj koji ne kapira nece mu pomoci ni ChatGPT. :-> Ostaje pitanje za koji je nivo ovaj zadatak? Pretpostavljam II srednje ili tako nesto, koliko se secam, mi smo u II srednje prvi put pomenuli pojmove trigonometrijskih funkcija, ali moguce je da su nastavni programi u BiH drugaciji, a postavljac teme je odatle. [ Living Light @ 17.03.2024. 13:45 ] @
Beri,
To je isti Q, kao na ETF-u (BG) kada iz matematike NAVALE profesori sa "Nikad Primenjenim" zadacima. Ubiju studenta U POJAM ! ... sa, Samo njima (profanima) "Korisnim" zadacima, student (ako Buba) završi Fax, zaposli se kod nas u firmi na "Porbni rad"..... (nema ono "moj rodjak sa sela", niti sin od strica iz grada), a u petak, .... vec mu saopštavamo: Nece Biti Produženo"! decko, 'ajde Ti traži neki posao gde se "SAMO Aplikacije eehhhbendišu" po ceo dan-svaki dan! Takvi radnici su NENAPLATIVI, - jer od Ljubičastog "Aplikation Inženjera" koji "Misli da SVE ZNA" nema Go. Quhhrrrac koristi. --------------------------------------- Nek' ON svoje "Šatro-Mile Sposobnosti" prodaje nekoj Firmi : Gde MOŽE po ceo dan da Ne Radi NIŠTA ! Naravno, Čast jako retkim izuzecima. Za skoro 37 god. staža, još nisam sreo Inženjera (ni u RS, ni u DE, ni u AU, a ni u HU kome trebata "Nebuloza od Lebdece Matematike" ... OSIM ako nece taj Student posle da PREDAJE isto SHHRRRANJE na tom Istom Faxu, zagorčavajući život Novim Studentima sa Teorijama "SAMO I SAMO iz PROFESOROVIH KNJIGA !!! ------------------------- Za integrale, diferencijale, limese --- Skidam Kapu ! [ nato_bot @ 17.03.2024. 20:25 ] @
Citat: B3R1 E sad, tu se verovatno dale treba cimati s onim silnim trigonomentrijskim formulama za dvostruke uglove i polovine ugla, jer je sqrt(3) kosinus ugla od 30 stepeni ... pa raznim trange-frange operacijama dodjes do rezultata. Zašto "trange-frange"? Cos(x) = a/4 ≈ 0.966 pa se iz tablice u udžbeniku očita ugao od 75 stepeni. To je zadatak za gimnaziju 1. razred. [ zzzz @ 17.03.2024. 22:39 ] @
Citat: B3R1: Pitanje nije kako resiti zadatak, vecina forumasa ce ti dati rezultat relativno brzo. Pitagora + kalkulator, par puta arccos() i arcsin() i dobijes uglove od 75 i 15 stepeni. Ovaj rezultat se može lako dobiti bez olovke i kalkulatora.U 5 jednostavnih koraka.Čak ne treba ni pitagora. [ dusanboss @ 18.03.2024. 14:07 ] @
Takaov trougao ne postoji. Ako a x b =4 onda nikako ne može a na2 + b na2 da bude 16.
[ djoka_l @ 18.03.2024. 14:18 ] @
Postoji, dušane.
Beri je dao i vrednosti za a i b. [ B3R1 @ 18.03.2024. 14:41 ] @
Citat: nato_bot: [pa se iz tablice u udžbeniku očita ugao od 75 stepeni. Tablice ili kalkulator - isto mu dodje. Citat: zzzz: Ovaj rezultat se može lako dobiti bez olovke i kalkulatora.U 5 jednostavnih koraka.Čak ne treba ni pitagora. Stvarno? Voleo bih da vidim to resenje u 5 jednostavnih koraka. Posto si postavio zadatak, verujem da znas i resenje. :-) [ zzzz @ 19.03.2024. 10:47 ] @
Ovaj zadatak je za VI osnovne,a rješilo ga je oko pola đaka u razredu.Ovo je bilo pod c),a cijeli zadatak izgleda ovako:
-Odredi uglove pravouglih trokutova ako su: a)obe katete jednake b)Hipotenuza 2x veća od kraće katete c)Hipotenuza je 4 ,a površina 2 a i b sam preskočio kao i ono VI da bi bilo nešto teže za rješavanje. [ djoka_l @ 19.03.2024. 11:18 ] @
Aha, a deca u 6. već koriste trigonometriju?
[ dusanboss @ 19.03.2024. 12:44 ] @
Citat: djoka_l: Postoji, dušane. Beri je dao i vrednosti za a i b. U pravu ste. I pomislo sam da će biti neki sa veoma malim uglom i dužom katetom približno 4. Nego sam nešto zeznao računajući iz glave. [ zzzz @ 19.03.2024. 12:57 ] @
Citat: djoka_l: Aha, a deca u 6. već koriste trigonometriju? Ne treba trigonometrija za one koji riješe zadatak pod b). [ dejanet @ 19.03.2024. 13:05 ] @
Mnogo je vremena proslo i ako sam imao tone trigonometrije u srednjoj i na faksu u raznim varijantama, ali se nesto ne secam da smo koristili (ako ikada) koristili kalkulator i te tablice ili izrazavali bilo koje resultate u stepenima, vec iskljucivo radiane (2*pi, pi, pi/2....) i tablice sa vrednostima tipa 1/2, sqrt(3)/2 ... itd.
Od svih postova ovde, jedino ovo sto je Beri poceo ima smisla, a za ostalo (bar u moje vreme) mislim da bi se proslo mnogo, mnogo lose na nekom kontrolnom ili ispitu. Prvo sto smo ucili relativno rano u srednjoj, jeste trigonometrijski krug kao osnovu cele ove price. [ B3R1 @ 19.03.2024. 14:57 ] @
Mislim da je Major dao zapravo najbolje resenje.
Osim sto je on iskoristio sinus, koji se ne uci u VI razredu, ali to je nebitno - deca u osnovnoj skoli znaju da ako je u nekom pravouglom trouglu hipotenuza 2 puta veca od (krace) katete, uglovi tog trougla su 30, 60 i 90 stepeni - prosto zato sto je takav trougao polovina jednakostranicnog trougla - tacnije jednakostranicni trougao presavijen po visini. U tavkom trouglu ugao naspram krace katete je 30 stepeni, sto znaci da je 2*alpha = 30 stepeni, odakle se dobija alpha = 15 stepeni, a drugi ugao je - logicno - 75 stepeni. Tako da ti ne treba ni T od trigonometrije. :-) Sve u svemu - lep zadatak ... Priznajem, radeci 30 godina jedan manje vise slican posao covek izgubi dosta tog detinjastog out-of-the-box razmisljanja koje ti je potrebno za ovakve zadacice. :-> [ zzzz @ 19.03.2024. 15:16 ] @
potpuno si u pravu,Major je trebao samo još ovo sodati:
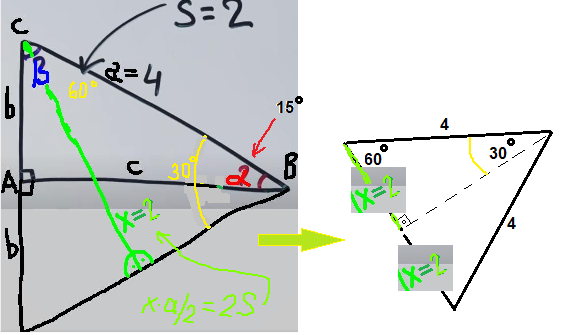 [ MajorFatal @ 22.03.2024. 14:31 ] @
Citat: B3R1: Osim sto je on iskoristio sinus, koji se ne uci u VI razredu, ali to je nebitno - deca u osnovnoj skoli znaju da ako je u nekom pravouglom trouglu hipotenuza 2 puta veca od (krace) katete, uglovi tog trougla su 30, 60 i 90 stepeni - prosto zato sto je takav trougao polovina jednakostranicnog trougla - tacnije jednakostranicni trougao presavijen po visini. U tavkom trouglu ugao naspram krace katete je 30 stepeni, sto znaci da je 2*alpha = 30 stepeni, odakle se dobija alpha = 15 stepeni, a drugi ugao je - logicno - 75 stepeni. Tako da ti ne treba ni T od trigonometrije. :-) Taman tako, bravo, ne treba ni trigonometrija .. samo ću ponoviti rešenje pošto se u međuvremenu izbrisalo .. E ako je za VI onda je lako, ja sam na tom nivou mentalno .. a = 4, b * c = 4 S(BCD) = (2b * c)/2 = (a * x)/2 -> 2bc = ax -> x = 2bc/a -> x = 2 sin(2alfa) = x/a = 2/4 = 1/2 -> 2alfa = 30 -> alfa = 15 beta = 90 - alfa = 90 - 15 = 75 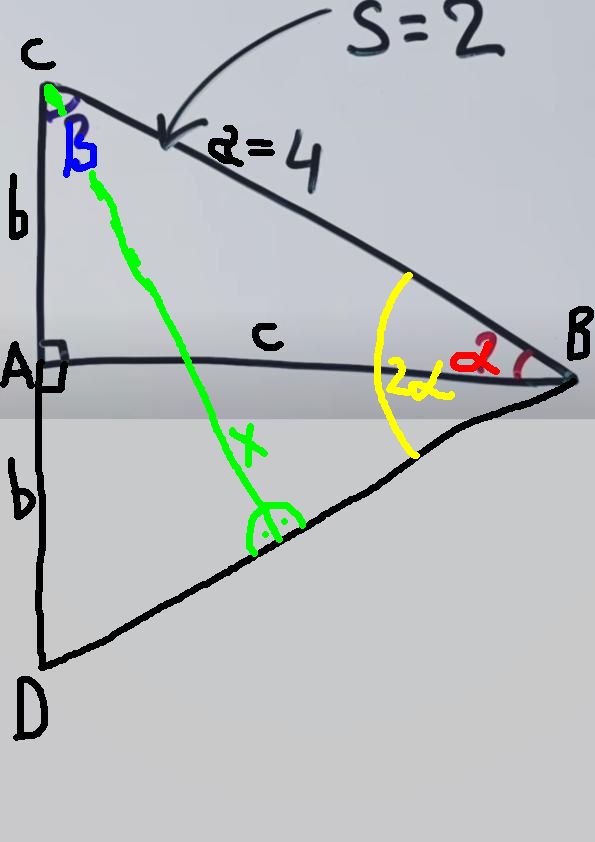 [ jans @ 14.04.2024. 20:14 ] @
Drugo rešenje:
Neka je tačka O središte hipotenuze, a D podnožje visine h=AD iz temena A na hipotenuzu. [att_img] Pošto je hipotenuza a=4cm a površina trougla 2cm2, sledi da je visina hipotenuze h=1. Učenici VI razreda znaju da odrede centar kružnice opisane oko trougla, a takođe znaju da je centar kružnice opisane oko pravouglog trougla središte hipotenuze, pa imamo da je OC=OA=OB=2. Pošto je pravougli trougao ADO polovina jednakostraničnog trougla ( AO=2AD ) sledi da je ugao kod temena O veličine 30o. Trougao ACO je jednakokraki a njegov spoljašnji ugao kod temena C znamo, sledi da su uglovi na osnovici tog trougla polovina spoljašnjeg ugla, pa dobijamo da je ugao kod temena C veličine 15o. [Ovu poruku je menjao jans dana 14.04.2024. u 21:49 GMT+1] Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|