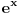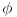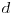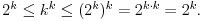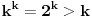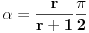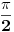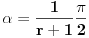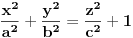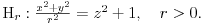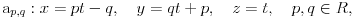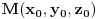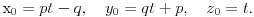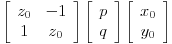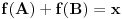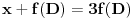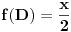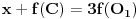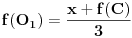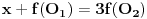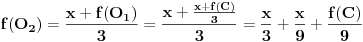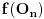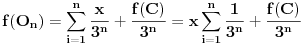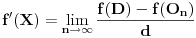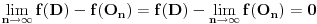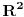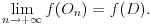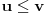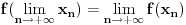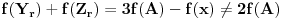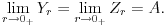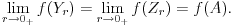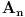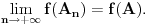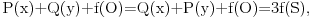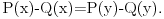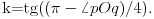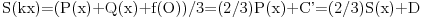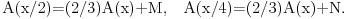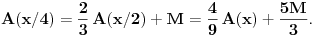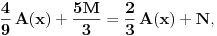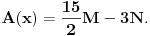|
|
[ Nedeljko @ 20.04.2004. 01:00 ] @
|
| Izgleda da niko ne prati temu "Stvarno teški zadaci, samo za najupornije". Tamo sam postavio dva zadatka čija rešenja niko nije dostavio. Štaviše, niko se nije ni interesovao za rešenja.
Kao prvi, navodim zadatak koji ne bi trebalo da bude preterano težak.
Podeliti ravan na beskonačno mnogo podskupova tako da bilo koja prava ima zajedničkih tačaka sa samo konačno mnogo od tih podskupova.
A kao dosta ozbiljniji, navodim sledeći zadatak.
Ispitati da li se prostor može predstaviti kao unija neke beskonačne familije pravih od kojih su svake dve mimoilazne.
Evo jednog isto vrlo teškog zadatka.
Pretpostavimo da smo svakoj tački A ravni xOy pridružili po neki realan broj f(A), ali tako da za ma koji trougao ABC u ravni xOy i centar O upisanog kruga u trougao ABC važi jednakost f(A)+f(B)+f(C)=3f(O). Dokazati da je svim tačkama ravni xOy pridružen isti realan broj, to jest da je funkcija f konstantna.
Mogu poslati i rešenja, ali ne bih da vam kvarim zabavu! |
[ srki @ 20.04.2004. 05:57 ] @
Citat:
Podeliti ravan na beskonačno mnogo podskupova tako da bilo koja prava ima zajedničkih tačaka sa samo konačno mnogo od tih podskupova.
Nacrtas u ravni liniju oblika funkcije 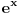 ili npr.  i svaku tacku te linije proglasis za podskupom. Ostatak ravni cini jedan skup.
Svi uslovi zadatka su zadovoljeni. Imamo beskonacno mnogo podskupova a svaka prava ima zajednickih tacaka samo sa konacno mnogo podskupova.
Za drugi moram da razmislim ali nemam bas vremena jer sam u guzvi a treci cu da procitam drugi put. [ Nedeljko @ 20.04.2004. 10:01 ] @
Da, Srki je korektno rešio prvi zadatak, ali naglašavam da su preostala daleko teža.
[ PeraT @ 21.04.2004. 22:11 ] @
Ispitati da li se prostor može predstaviti kao unija neke beskonačne familije pravih od kojih su svake dve mimoilazne.
Pa ni ovaj nije nesto tezak (ako si konstruktivan).
npr. odaberemo neku proizvoljnu pravu u tom prostoru pa
onda za familiju uzmemo skup svih njoj paralelnih.
p.s. Samo se nesto ne secam, jel mimoilazne prave smeju biti
paralelne?
pozdr.
[ Bojan Basic @ 21.04.2004. 22:56 ] @
Naravno da paralelne prave nisu mimoilazne.
Nedeljko, meni je za taj zadatak pala na pamet jedna ideja koju još nisam razradio, ali pogledaj, možda sam na dobrom putu.
Odaberemo proizvoljnu ravan i sve ravni paralelne sa njom. Uzmemo jednu zajedničku normalu svih tih ravni, i uzmemo jednu pravu u jednoj ravni tako da se seče sa tom normalom. To će nam biti prva prava, a ostale (u ostalim ravnima) dobijamo rotacijom njoj paralelne prave u odgovarajućoj ravni za ugao 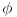 , gde je  , 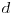 je udaljenost odgovarajuće ravni od one fiksne ravni pri čemu ukoliko "idemo na jednu stranu" rotiramo u jednom smeru, a u suprotnom rotiramo u drugom smeru. Znači, u svakoj ravni po jedna prava. Nadam se da shvataš kako sam ovo zamislio, izgleda slično kao burgija. Time smo dobili familiju međusobno mimoilaznih pravih koje pokrivaju ne znam tačno šta, ali bar mi reci da li sam dobro krenuo pa ću nastaviti da razmišljam. [ Nedeljko @ 21.04.2004. 23:12 ] @
Dakle, dobio si "burgiju", a treba da dobiješ ceo prostor.
[ PeraT @ 21.04.2004. 23:22 ] @
Da da, lupio sam glupost, ali nadam se da cu sa narednih par
linija nadoknaditi gornji propust.
Moje je misljenje da takva familija ne postoji. Jer ako bi ona
postojala kardinalnost skupa tacaka prostora dobijenog uniranjem
pravih bi bio cc. E sad pitanje je da li postoji bijekcija izmedju
ovog skupa i skupa realnih brojeva. Koliko se ja secam kursa
matematicke analize bijekcija NE POSTOJI. Mozda sam i ovde
omanuo (kao kod pravih), u kojem slucaju se izvinjavam na
lupanju gluposti.
Dakle kljucno pitanje je da li je cc istog reda kao i c?
(to da tacaka ima cc je manje vise lako dokazivo)
pozdr.
[ Bojan Basic @ 21.04.2004. 23:27 ] @
Pa znam da treba da dobijem ceo prostor, moje pitanje je bilo da li sam krenuo da razmišljam u pravom smeru ili ta "burgija" koju sam dobio nema baš nikakve veze sa rešenjem?
[ Nedeljko @ 21.04.2004. 23:45 ] @
Ako je k bilo koji beskonačan kardinal, onda je
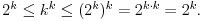
Ovde se koristi teorema o idempotentnosti beskonačnih kardinala po kojoj je k 2=k za svaki beskonačan kardinal k. No, sada je po Kantor-Bernštajnovoj teoremi k k=2 k, što je po Kantorovoj teoremi o partitivnom skupu više od k, tako da je 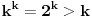 za svaki beskonačan kardinal k, pa i za c.
Međutim, kod nas će unija kontinuum mnogo pravih biti kardinalnosti kontinuum puta kontinuum, a to je kontinuum, tako da ti kardinalna aritmetika ovde neće ništa dati jer nigde nemaš stepenovanje, već samo množenje. To sledi i iz činjenice da prostor jeste unija familije disjunktnih pravih, kao na primer familije svih pravih paralelnih jednoj. E, jedini je problem što prave iz pomenute familije neće biti mimoilazne.
Za "burgiju" ne znam da li može dati rezultate. [ Nedeljko @ 22.04.2004. 08:44 ] @
Ajd, malo da pomognem. Tražena familija pravih postoji.
[ Nedeljko @ 25.04.2004. 10:26 ] @
Evo, još 14 sati i isteći će punih 7 dana otkako sam postavio ove zadatke. Treba li da dam neki hint ili da postujem kompletna rešenja?
[ Bojan Basic @ 25.04.2004. 13:03 ] @
Pa, ja bih predložio prvo samo hint. Zadaci mi deluju interesantno ali sam se zaglavio, jedino što mi je palo na mapet je ona "burgija" za koju si rekao da ne vodi ka rešenju.
[ filmil @ 25.04.2004. 13:54 ] @
Hm, da probam da odgovorim na popunjavanje prostora pravama.
U proizvoljnoj ravni uočimo kružnu liniju sa centrom O i poluprečnikom r. Postavimo (recimo) polarni koordinatni sistem tako da svakoj tački na (O,r) odgovara jedna vrednost ugla 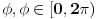 .
Za neko  , povučemo tangentu t na (O,r) u odgovarajućoj tački (nazovimo je T) i konstruišemo ravan normalnu na početnu ravan a koja sadrži t; zatim u toj ravni konstruišemo normalu n na pomenutu tangentu. Presek n i t neka je opet tačka T.
Zatim opet u ovoj poslednjoj ravni postavimo pravu s pod nekim uglom 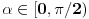 u odnosu na n, a seče n i t u tački T.
Dobili smo pravu „zakačenu pod uglom“ za (O,r).
Ako prošetamo  kroz sve moguće vrednosti domena, dobijamo površ koju ću u nedostatku znanja nazvati „dvostruka kragna“. U svakoj ravni paralelnoj sa početnom a na rastojanju d od nje, ona generiše jedan krug, poluprečnika ne manjeg od r (ako se nisam prešao, poluprečnik je  . U svakoj ravni na rastojanju d od početne, svaka prava generiše samo po jednu tačku, tako da se prave ne seku, ali s obzirom na način na koji su generisane, ne mogu biti paralelne.
Sada zavežemo ugao i poluprečnik jedan za drugi tako što kažemo 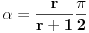 , i poluprečnikom r prošetamo se po skupu  , ubacujući sve „kragne“ i pripadajuće prave u traženu familiju pravih.
Pošto je onaj tangens odozgo strogo rastući na rečenom podskupu, to su sve kragne disjunktne, a pošto je  različit u svake dve kragne, to je nemoguće da bilo koje dve prave iz dve kragne budu paralelne.
Na kraju verovatno još treba proturiti jednu pravu koja odgovara slučaju r=0.
f
[ Nedeljko @ 25.04.2004. 14:10 ] @
Za "burgiju" nisam rekao da ne vodi ka rešenju, već da ne znam da li vodi ka njemu. To je drugo. Ja sam time rekao samo da ja ne znam kako bih "burgiju" iskoristio da dođem do rešenja.
Što se tiče hinta, sačekaću još malo. Postovao bih ga do ponedeljka 27.4.2004. u 02:00 noću, naravno, ako se ne javi neko ko ne bi želeo da mu kvarim zadovoljstvo. Ako se neko takav javi, onda bih rešenje i hint još odložio.
Međutim, čudno mi je da nema interesovanja za treći zadatak. Prvi je vrlo brzo rešen, oko drugog se ljudi još uvek (koliko toliko) javljaju, a treći kao da nikoga ne zanima.
Mogao bih čak da postujem familiju pravih koja predstavlja jedno od mogućih rešenja za koju je vrlo lako utvrditi da ispunjava tražene uslove, ali pri čemu ne bi bilo jasno kako se dolazi do nje ako to ne bih opisao.
Dakle, mogu da postujem hint preko koga se može doći do rešenja (postupno), što bi bila prva varijanta; mogu da postujem familiju pravih za koju se vrlo jednostavno preoverava da ispunjava tražene uslove (takvo kompletno rešenje je vrlo kratko), pri čemu bi rešavači trebali da odgonetnu postupak kojim se dolazi do te familije, što bi bila druga varijanta; mohu takođe i da postujem rešenje koje uključuje i postupak kojim se stiže do te familije (e, to je već znatno duže), što bi bila treća varijanta.
U svakom slučaju, očekujem predloge ostalih rešavača.
[ stalker @ 25.04.2004. 18:34 ] @
Ma, OK, ne treba jos ni resenja ni hintove da postujes. Sta kazes na Filipove kragne? A za treci, koliko sam ukapirao na es-u, rade se zadaci redom kojim su napisani (bar meni tako izgleda). Cekaj da ljudi oglodju ovaj drugi , pa ce se bace(imo) na treci
[ Nedeljko @ 25.04.2004. 20:34 ] @
BRAAAAAVOOOOO, BRAAAAVIIISIIIMOOOOOOOOO!
Sve čestitke Filipu za rešenje. Čak je idejno identično onom koje sam hteo da postujem. Ipak, Filopvo rešenje ima jedan mali bagčić. Naime, ugao bi trebao da opada od 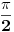 do 0 kada r raste od 0 do 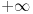 da se "dvostruke kragne" ne bi sekle. Može se koristiti na primer veza 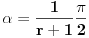 . To je sve što imam da ispravim u Filipovom rešenju. E pa Filipe, svaka ti čast, nemam šta drugo da kažem (tj. napišem).
Inače, površ čija je kanonska jednačina 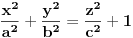 se zove jednograni (ili eliptički) hiperboloid. Filipova "dvostruka kragna" je zapravo kružni hiperboloid, tj. specijalan slučaj čija je kanonska jednačina  . Inače, jedan moj drug zove jednograni hiperboloid "kukić strukić"!
Jednograni hiperboloid ima sledeće fundamentalno svojstvo: Kroz svaku tačku jednogranog hiperboloida prolaze tačno dve prave koje cele leže na tom hiperboloidu. Zato ga možemo predstaviti kao uniju disjunktnih pravih. To se još izražava rečima: "Jednograni hiperboloid je 2-mnogostrukost". Upućeniji ne treba da pojam n-mnogostrukosti pomešaju sa pojmom n-dimenzione mnogostrukosti. To su potpuno različiti pojmovi.
Dovoljno je sada da izaberemo po jednu pravu kroz svaku tačku na npr. malom krugu te površi (od kojega je Filip pošao) povučemo jednu od tih pravih, ali da ih uvek "češljamo" na istu stranu.
Sada se ceo prostor bez izabrane prave p može predstaviti kao disjunktna unija kružnih hiperboloida sa osom p, a svaki od njih kao disjunktna unija pravih. Jasno je da će sve one biti međusobno disjunktne, kao i da su mimoilazne sa p. No, da dve prave iz disjunktnih hiperboloida sa istom osom p nikada ne bi bile paralelne, potrebno je da se u navedenom kanonskom obliku isti količnik r/c ne
"ponovi dvaput".
Planirao sam da postujem sledeću familiju hiperboloida:
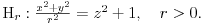
Tada bi se kao odgovarajuća familija pravih dobila familija pravih
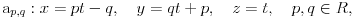
datih u parametarskom obliku. Veza između parametara p,q i r data je sa  . Za p=q=0 se dobija zajednička osa svih tih kružnih hiperboloida. To je ona prava koja se na kraju dodaje.
Hajde da direktno proverimo da ova familija pravih ispunjava tražene uslove. Neka je 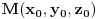 proizvoljna tačka prostora. Da bi tačka M pripadala pravoj 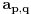 potrebno je i dovoljno da za neko t važi
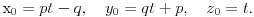
No, za t i nemamo mnogo izbora, pa zapravo treba da važi

ili u matričnom obliku
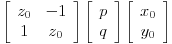
To je sistem od dve linearne jednačine po p i q sa determinantom  koja je uvek različita od nule, pa imamo jedinstveno rešenje po p i q. Drugim rečima, svaka tačka prostora pripada tačno jednoj od pravih iz naše familije.
To znači da smo pokupili sve tačke prostora i da su sve prave iz te familije disjunktne. Treba samo još proveriti da nikada nisu paralelne (jer se zbog disjunktnosti ne mogu seći). No, vektor prave 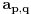 je (p,q,1), a vektori (p,q,1) i (p',q',1) su kolinearni ako i samo ako je p=p' i q=q', čime je dokaz završen.
Još jednom sve čestitke za Filipa, a ja bih samo još da naglasim da sam svoj prethodni post pisao dok je Filip slao svoje rešenje, pa u trenutku slanja posta nisam znao da je nako u međuvremenu dostavio rešenje.
[ Nedeljko @ 25.04.2004. 22:17 ] @
Ja ti se Filipe iskreno izvinjavam. Budući da si pod uglom  podrazumevao ugao između prave koju konstruišeš i normale n, onda taj ugao zaista treba da raste od 0 do 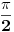 kada r raste od 0 do 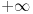 , pa na tvoje rešenje nemam nikakvih primedbi. Bila je moja greška. Mislio sam da ti je  ugao između prave koju konstruišeš i polazne ravni. To bi bila druga stvar.
Još jednom ti se izvinjavam i koristim ovu priliku da ti još jednom čestitam! [ stalker @ 26.04.2004. 19:43 ] @
Da pokusam treci. Ne verujem da je tacno, ali mozda nekom pametnijem dam ideju.
Odaberemo proizvoljan trougao u x0y (tako da sve sto dobijem vazi za sve trouglove i tackice). Stranice sam obelezio sa A,B,C,tu su jos tacke 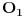 (poluprecnik upisanog) i D (sredina AB).
Cela ideja je sledeca: Uzimamo dve tacke koje su blizu, nadjemo diferencijal te funkcije,i ako dobijemo 0, f-ja je konstantna, a posto ce sve vaziti za sve trouglove, f-ja je svuda konstantna. Trouglove cu smanjivati/generisati na sledeci nacin: Prvi trougao je ABC, drugi je 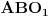 , treci je  ( 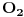 je centar trougla 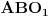 )... Moze se pokazati da je (citaj: mrzi me da pisem)
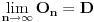
( 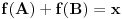 u daljem tekstu)
Dalje, u granicnom slucaju, za patoloski trougao ADB vazi:
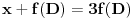
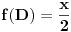
Hajde sad da krenemo od onog ABC
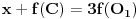
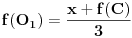
Za sledeci imamo
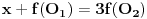
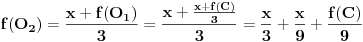
Da ne pisem dalje, nas zanima 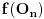 koji glasi:
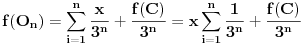
Necemo odma' da ganjamo n u beskonacno nego ovako:
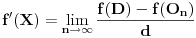 sto je diferencijal, a on ce biti jednak nuli ako
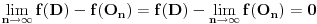
Sada kada pogledate onaj red, lako se dobija (citaj: mrzi me da pisem) da je ovaj diferencijal stvarno nula, tj da je funkcija konstantna za sve tacke
Q.E.D.    [ Nedeljko @ 26.04.2004. 20:15 ] @
Moram da napomenem da ovde nema nikakvih dodatnih pretpostavki o funkciji f, kao što je neprekidnost, diferencijabilnost ili nešto slično, tako da se taj aparat ne može primenjivati na funkciju f, osim ako se dokaže da ona pod navedenim pretpostavkama mora biti takva. Naravno, ona mora biti čak konstantna (što treba dokazati), a konstanta je neprekidna, glatka itd. tako da dokaz diferencijabilnosti nije nemoguć, ali se takve osobine mogu koristiti tek pošto se dokažu.
Inače, nisam baš razumeo oznake X i d iz ponuđenog rešenja, a ima i mesta na kojima se ne dokazuje nešto što je važno. Nije isključeno da se to lako vidi, budući da sam ja glup, ali mi izvođenje nije baš sasvim jasno. No, čak i da je dobro, to bi bilo rešenje samo za slučaj kada je f diferencijabilna funkcija koja slika ravan  u R.
No, raduje me da ljudi razmišljaju o ovom problemu. [ stalker @ 26.04.2004. 22:13 ] @
X je greska, a d sam napisao za udaljenost od D do  mada to nije sada tako bitno:) [ Nedeljko @ 26.04.2004. 23:49 ] @
I dalje ne vidim odakle je izvod konstantno jednak nuli, a i da jeste pod pretpostavkom diferencijabilnosti funkcije f, mi tu pretpostavku nemamo. Memamo ni pretpostavku neprekidnosti, pa ni limes nisi mogao da koristiš u redu
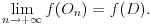
Prekoračio si sredstva. Mi NE ZNAMO ni da je funkcija f neprekidna, već samo da ima pomenutu osobinu iz formulacije zadatka. [ Mihailo Kolundzija @ 27.04.2004. 09:19 ] @
Buduci da u poslednje vreme mnogo gresim, moguce je da sam i sad polupao neke loncice, ali cu ipak da napisem nesto sto mi je palo na pamet.
Imamo neke tri tacke A, B i C i centar opisanog krugao O. Na kruznici sa centrom u O na kojoj su A, B i C izaberemo tacku S, i posmatramo trouglove ABS, BCS i ACS. Na osnovu uslova zadatka, imamo da je f(C) = f(S), f(B) = f(S) i f(A) = f(S), sto ce reci da je f konstatno na pomenutoj kruznici i iznosi f(O). Stvar naravno vazi za bilo koju kruznicu sa centrom u O.
Jesam li na dobrom putu, ili sam negde pogresio?
[ Nedeljko @ 27.04.2004. 10:00 ] @
U zadatku O nije centar OPISANOG, već UPISANOG kruga u trougao ABC. Ovo bi bilo rešenje zadatka koji bi se dobio zamenom reči "upisanog" rečju "opisanog" u postavljenom zadatku, koji je daleko lakši. No, ovde je postavljen drugačiji zadatak.
[ srki @ 27.04.2004. 11:41 ] @
Imamo neke tri tacke A, B i C i centar upisanog kruga O. Pretpostavimo da je f(A)< f(B) i f(A)<f(C) sada izbacimo tacku B ili C kod koje je f-ja veca i umesto te tacke uzmemo O. Posmatramo taj trougao. Uradimo istu stvar i tako nastavimo u beskonacnost. Na kraju ce ili druge dve tacke da se priblizavaju tacki A pri cemu ce limes funkcije tih tacaka biti jednak f(A). To se lako pokazuje pa necu to da razglabam sada. Jedino ako se trazi.
E sada uzmemo neku tacku X koja je razlicita od A i cija je vrednost razlicita od f(A) .
Onda opisemo krug oko A sa nekim malim poluprecnikom r. Napravimo jednakokraki trougao kod koga je vrh tacka X a centar upisanog kruga je A. Te dve tacke nikada ne menjamo. Upisani krug ima poluprecnik r. Uzmemo i smanjujemo taj pokuprecnik i dobicemo dve tacke koje se priblizavaju tacki A ali ciji je zbir jednak 3*f(A)-f(X) sto je nemoguce ako je limes vrednosti funkcija jednak f(A) jer bi zbir onda trebalo da se priblizava 2*f(A).
To sve znaci da je pocetna pretpostavka pogresna da je f(A)<f(B) i manje od f(C).
[Ovu poruku je menjao srki dana 28.04.2004. u 03:25 GMT]
[ srki @ 27.04.2004. 12:01 ] @
Cini mi se da imam malu gresku u dokazu i da one dve tacke ne moraju da se priblizavaju tacki A vec nekoj drugoj tacki ali dalje je slicno samo sto biramo tu tacku umesto A.
[ Nedeljko @ 27.04.2004. 12:27 ] @
Koliko ja shvatam, ti si oko tačke A opisao krug poluprečnika r na kome možeš da uočiš tačku X za koju je f(X) različito od f(A) i onda si na tom istom krugu uočio na primer tačke Y i Z za koje je f(Y)+f(Z)=3*f(A)-f(X). Smanjivanjem poluprečnika dobijaš nizove X n,Y n,Z n koji konvergiraju ka A, i za koje je f(Y n)+f(Z n)=3*f(A)-f(X n). No, čak i ako je f(A)>f(Y n),f(Z n), tu i dalje nema očigledne kontradikcije.
Naime, ako je u n<u n za sve n, onda u opštem sličaju ako nizovi u n i v n konvergiraju ka u i v tim redom, važi 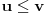 i uopšte ne mora da bude u<v. Najjednostavniji primer je u n=0, v n=1/n. Morao bi da pojasniš konstrukciju. Takođe, vodi računa da neprekidnost funkcije f nije pretpostavka zadatka tako da stvari kao što je 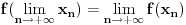 možeš da koristiš samo u situaijama u kojima možeš to da obrazložiš. Ako to dokažeš za konvergentne nizove određenog tipa, onda pazi da to koristiš samo za takve nizove. [ srki @ 27.04.2004. 13:21 ] @
Nema tacaka Xn. X i A su mi konstantne. Samo smanjujem poluprecnik r. posto je f(X) razlicito od f(A) onda je i 3*f(A)-f(X) razlicito od 2*f(A) cemu bi konvergirao zbir funkcija one dve tacke koje priblizavamo tacki A.
Znaci smanjujemo poluiprecnik r i pravimo jednakokraki trougao tako da je jedna stranica normalna na pravu XA.
Bio sam napravio lapsus pa sam u prethodnom odgovoru napisao jednakostranicni trougao umesto jednakokraki.
[ srki @ 27.04.2004. 13:46 ] @
Citat: Nedeljko:
Takođe, vodi računa da neprekidnost funkcije f nije pretpostavka zadatka tako da stvari kao što je 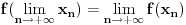 možeš da koristiš samo u situaijama u kojima možeš to da obrazložiš.
Nisam to nigde koristio. To se dobije kao rezultat. Ako imamo 3 tacke x,y,z i ako je f(z) najvece a recimo f(x) najmanje onda ce u sledecoj iteraciji vrednost f(O) da se smanji za
(f(z)-(f(x)+f(y)+f(z))/3 )/3 i tako dalje sto znaci da ce lim f(O) biti jednak f(x) kako idemo kroz iteracije.
[ Nedeljko @ 27.04.2004. 15:11 ] @
Koliko sam te shvatio posle tvojih poslednjih postova, ti si fiksirao A i X i tako da f(A) i f(X) budu različiti, i za dato r>0 izabrao tačke Y r i Z r tako da trougao XY rZ r bude jednakokraki i da upisani krug u taj trougao ima centar A i poluprečnik r. Tada bi zaista moralo da važi 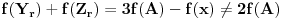 , kao i
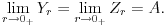
No, i dalje ne vidim zašto bi moralo da bude
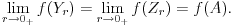
Ako ovo obrazložiš, rešio si zadatak u potpunosti. Voleo bih da vidim kako se ono tvoje zaključivanje primenjuje na tačke X,Y r,Z r i A budući da ti je ovde centar upisanog kruga konstantan.
No, napredak je ostvaren obzirom da imamo rešenje koje je u potpunosti korektno barem u slučaju neprekidne funkcije f. [ srki @ 27.04.2004. 16:04 ] @
Citat: Nedeljko:
Koliko sam te shvatio posle tvojih poslednjih postova, ti si fiksirao A i X i tako da f(A) i f(X) budu različiti, i za dato r>0 izabrao tačke Yr i Zr tako da trougao XYrZr bude jednakokraki i da upisani krug u taj trougao ima centar A i poluprečnik r.
Tako je!
Citat:
.
..
...
....No, i dalje ne vidim zašto bi moralo da bude
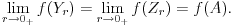
Ako ovo obrazložiš, rešio si zadatak u potpunosti.
Pa to vazi zbog nacina na koji smo izabrali tacku A. U prvom postu sam objasnio kako mora u nekoj okolini tacke A da funkcija tezi ka f(A) jer se pri svakoj iteraciji (biranje novog temena trougla) funkcija od novog centar upisanog kruga je smanjena za (f(Zn)-(f(A)+f(Yn)+f(Zn))/3 )/3 (kada se izracuna, a pri tome smo izbacili tacku Zn i zamenili sa prvim O). Znaci funkcija se stalno smanjuje , ogranicena je odozdo sa f(A) a takodje ne moze da tezi nekom drugoj vecoj vrednosti k jer bi se vec u sledecoj iteraciji smanjili za (k-((f(A)+(k)+(k)/3))/3=(k-f(A))/9. Znaci k mora da bude jednako f(A).
Naravno ovo sto sam napisao nije strogo matematicki napisano ali se razume postupak i nacin razmisljanja. [ Nedeljko @ 27.04.2004. 16:42 ] @
U svom prvom postu si NAŠAO barem jedan niz tačaka 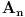 koji teži tački A i takav da je 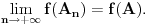 I dalje ne vidim zašto mora to da važi za SVAKI niz koji teži tački A. Pokušaj zato da to svoje rasuđivanje primeniš na konvergenciju duž krive koju opisuje tačka Y r kada r teži nuli sa gornje strane. [ srki @ 27.04.2004. 22:25 ] @
Da, u pravu si. Razmislicu drugi put o resenju posto sam sada na poslu.
Pozdrav
[ Nedeljko @ 02.05.2004. 17:24 ] @
Za manje od osam sati proći će 14 dana otkako sam postavio zadatke. Treba li da postujem rešenje preostalog zadatka ili neki hint?
[ Nedeljko @ 03.05.2004. 01:59 ] @
Uočimo proizvoljnu tačku O poluprave p i q sa temenom O koje ne leže na jednoj pravoj. Za realan pozitivan broj x sa p x označićemo tačku poluprave p koja je na rastojanju x od tačke O, a sa q x tačku prave q koja je na rastojanju x od tačke O. Definišimo još funkcije P(x) i Q(x) sa P(x)=f(p x), Q(x)=f(q x). Sa s označimo simetralu ugla pOq. Za proizvoljne x,y>0 centar upisanog kruga S u trougao Op xq y se nalazi na pravoj s, pa se refleksijom u odnosu na pravu s preslikava u sebe. Ista refleksija prevodi tačku p x u tačku q x, kao i tačku q y u tačku p y. To tačno znači da trouglovi Op xq y i Oq xp y imaju zajednički centar upisanog kruga S (jer izometrija prevodi centar upisanog kruga u centar upisanog kruga) pa važi
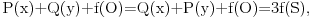
odnosno posle skraćivanja sa f(O) i sređivanja
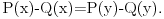
No, budući da su x i y bili proizvoljni pozitivni realni brojevi, ovo tačno znači da je funkcija P(x)-Q(x) konstantna. To upravo znači da je P(x)=Q(x)+C za neku konstantu C. Ovo znači da ako uočimo bilo koje dve poluprave sa zajedničkim temenom, funkcija f se na tim polupravama "razlikuje za konstantu" koja naravno zavisi od izabranih polupravih.
Označimo sada sa s x, gde je x pozitivan realan broj tačku na pravoj s koja pripada konveksnom uglu sa kracima p i q i koja je na rastojanju x od tačke O. Definišimo funkciju S(x) sa S(x)=f(s x). Pretpostavimo da je S(k) centar upisanog kruga u trougao Op xq x za x=1. Može se pokazati da je zapravo
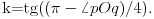
No, tada iz činjenice da sličost prevodi centar upisanog kruga u centar upisanog kruga i iz prethodnog razmatranja sledi da za svako x>0 važi formula
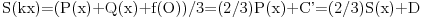
za neke konstante C' i D. Ovde je naravno korišćena činjenica da se finkcija f na polupravama p,q i s "razlikuje samo za konstantu". Mi smo to dokazali za poluprave p i q, ali pošto su one bile proizvoljne nekolinearne poluprave sa zajedničkim temenom, isto će važiti i za poluprave p,q i s.
Uočimo sada proizvoljnu polupravu a sa temenom O i poluprave b i c, takođe sa temenom O takve da poluprave a i b zaklapaju ugao (pi/2)-2 arctg(1/2), a poluprave a i c ugao (pi/2)-2 arctg(1/4). Na način kao gore zaključuje se da postoje konstante M i N takve da uz sličnu simboliku kao gore za svako x>0 važi
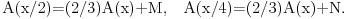
Iz prve jednakosti sledi da je i 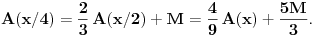 Ta jednakost zajedno sa drugom od gore navedenih jednakosti daje 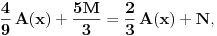 odakle najzad sledi 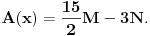 To upravo znači da je na polupravoj a funkcija f konstantna. Međutim, pošto je a bila proizvoljna poluprava sa proizvoljnim temenom O, to će značiti da je funkcija f konstantna na svakoj polupravoj, a kako se svake dve tačke nalaze na nekoj polupravoj, odatle odmah sledi da funkcija f ima istu vrednost u bilo kojim dvema tačkama, to jest da je konstantna.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|