[ test1234 @ 22.05.2024. 06:51 ] @
|
[ MajorFatal @ 22.05.2024. 21:53 ] @
Ne bih se upisao :)
Šta ako tačan odgovor zaokružim crnom hemijskom olovkom? Šta ako mi se u poslednjih 15 minuta sloši i baš moram da izađem? Zadatak broj 3 mislim da je odgovor D, a zadatak broj 5 da je G ... [ djoka_l @ 23.05.2024. 08:53 ] @
Stvarno su genijalci oni koji upišu MG.
Moja generacija nije imala prijemni, upisivala se od trećeg rezreda, samo uspeh iz škole i sa takmičenja. A zadaci, svaki ima zez. 1. C - ovo je verovatno najlakši od svih, samo treba da se uradi bez digitrona. Odmah se vidi da rezultat treba da bude negativan, samo ne smeš da se zezneš 2. D - stvarno problematičan ako nemaš rutinu. Treba imati kliker pod pritiskom i provaliti da je prvi izraz pod korenom (a+b)^2 a drugi (c-b)^2 3. C - ja sam se tu zeznuo, označio sam A, a treba C. našao sam da 1237 treba da budu ciframa, a 1 mora na prvo mesto pa je onda rezultat 6. Smetnuo sam sa uma a i brojevi 1167 daju još 6 na rezultat 4. D - jasno je da je poslednja cifra neparna. Prvi član uvek daje 6 na kraju, a drugi i treći imaju cikluse koji su pravilni. Potrebno je da se razumeš u modulo račun 5. G - ovo je isto bio relativno lak x-x*0.9*0.95 = 9860 6. B - namerno su napravii da deluje teže nego što jeste. Kažu paralelogram, što unosi zabunu. Ako rezultat važi za SVAKI paralelogram, onda važi i za pravougaonik stranica 9 i 6. Samo je u tome caka, ne rešavati za SVAKI paralelogram, nego za pravougaonik 7, 8, 10, 11 nisam ni pokušao da rešim 9. E - n=8m/(m-8) (m,n) pripada skupu {(9,72), (10,40), (12,24), (16,16)} 12. H - e tu sam baš bio u rebusu, dobio sam 1152, a to nije bilo ponuđeno. Računao sam, da bi knjige bile nesusedne, treba ih posaviti na parna mesta ili na neparna (1,3,5,7) ili (2,4,6,8). U stvari postoji 5 rasporeda, a ne dva (1,3,5,7), (1,3,5,8)(1,3,6,8), (1,4,6,8), (2,4,6,8). Na svakom od tih rasporeda knjige iz matematike se rasporede na 4! permutacija, a ostale knjige na 4!, pa je ukupan broj rasporeda 4!*4!*5 = 576*5 = 2880 [ nato_bot @ 23.05.2024. 10:54 ] @
Pa 8-mi možeš napamet. Isčupaš korenje i dobiješ nešto kao |2x-3| ≤ 7.
-2 ≤ x ≤ 5 Brojeći na prste tu ima 8 celobrojnih rešenja. [ djoka_l @ 23.05.2024. 14:00 ] @
Ne kažem da su ovi zadaci koje nisam rešio teški, samo ih nisam rešavao.
Sve sam pisao na praznom delu jedne koverte, pa nisam imao mesta Ono što mi je fascinantno je to da zadatke treba da reše osmaci. Ni jedan nije toliko jednostavan, da osmak može da reši bez naprezanja vijuga. [ djoka_l @ 23.05.2024. 15:32 ] @
Citat: nato_bot: Pa 8-mi možeš napamet. Isčupaš korenje i dobiješ nešto kao |2x-3| ≤ 7. -2 ≤ x ≤ 5 Brojeći na prste tu ima 8 celobrojnih rešenja. By the way, deca u osnovnoj školi rešavaju ove zadatke na sledeći način Kada se iščupa korenje, dobije se |x + 1| + |x - 4| Onda se proveri znak za x<-1, x između -1 i 4, pa x >4 Dobiju da je za x<-1 onaj zbir 3-2x, za x između -1 i 4 dobiju da je rezultat 5 (ne zavisi od x), a za x>4 rezultat je 2x-3 Tvoje rešenje, je naravno, tačno, ali nije tačno da je na celom opsegu |2x - 3| nego je konstantno na [-1,4] [ mjanjic @ 23.05.2024. 16:00 ] @
Citat: djoka_l: 2. D - stvarno problematičan ako nemaš rutinu. Treba imati kliker pod pritiskom i provaliti da je prvi izraz pod korenom (a+b)^2 a drugi (c-b)^2 Zavisi kako se gleda, može da bude: 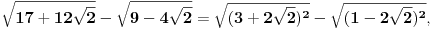 ali, može da bude i: 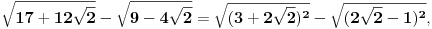 međutim kod prvog slučaja ne sme tek tako da se skrati koren i kvadrat ili da zamene mesta, odnosno može ako se postupi kao kod uklanjanja znaka apsolutne vrednosti, tj. sve se pomnoži sa 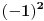 . .Možda je trik u tome da se neko eventualno zezne i tako dobije rešenje pod G, tj. 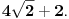 [ djoka_l @ 23.05.2024. 18:05 ] @
U pravu si, nisam razmišljao o tome.
Kada sam video da su u odgovorima ponuđena celobrojna rešenja, "namestio" sam izraze pod korenom da mi se skrati član sa korenom iz dva. To je ono, kada više ideš po osećaju kako treba da izgleda rešenje, nego ako se stvarno udubiš. [ X Files @ 23.05.2024. 20:07 ] @
Citat: djoka_l: Ono što mi je fascinantno je to da zadatke treba da reše osmaci. Ni jedan nije toliko jednostavan, da osmak može da reši bez naprezanja vijuga. Komentarišem sad nešto, što sigurno i sam znaš, samo se nadovezujem na tvoj komentar... Ove zadatke pre svega rešavaju đaci osmaci, koji su u 7 i 8 razred osnovne škole završili pri matematikoj gimnaziji, i to sa glavnim ciljem - položiti bas ovaj ispit. I to rade "kao od šale", često sa maksimalnim brojem bodova. To je zaista sjajno i za respekt. Jednom sam u sali rekao, treba im odmah pisati diplomu fakulteta. Ako se ne varam procenat uspeha je bio 48 od 50. To je sasvim drugi nivo performansi u odnosu na djake klasicnih gimanzija, u kojima, ma koliko neki djak bio inicijalno talentovan i naprezao vijuge - nece mu puno pomoci. Za ove zadatke treba i znanje i kondicija, koja se stice pre svega sistemskim radom. Kada se radi uz odlicne profersore, u ozbiljnoj konkurenciji, matematicke listove i pripremnu mentorsku nastavu (besplatnu i komercijalnu), uspeh je prilicno izvestan. Podrazumeva se da ta deca u 7 razred osnovne skole pri matematickoj gimnaziji nisu bas upali slucajno. Inicijativa cesto ide i iz kuce, od roditelja... Pre 10-tak godina, bio sam prilicno verziran za resavanje zadataka ovog nivoa, jer sam klinca spremao za neka takmicenja. Pokusao sam da i sam uradim tih 12 zadataka u zadatom roku, i ne secam se da sam ikada uspeo da uradim sve bez greske. Obrni okreni, makar 2 sam zasrao. [ jans @ 23.05.2024. 21:09 ] @
Najpre napomena u vezi 6. zadatka. Ako učenici ne uoče da zadatak mogu rešiti onako kako predlaže djoka_I, zadatak rešavaju u opštijem obliku.Ni taj način nije mnogo teži. Trougao određen simetralom unutrašnjeg ugla paralelograma jeste jednakokraki ( treba iskoristiti transverzalne uglove, a transverzala je simetrala ). Put do rešenja je sličan postupku sa pravougaonikom, a razlika je u tome što ne znamo dužinu zajedničke visine trougla i trapeza ( ta dužina nije bitna pošto se u količniku visina skrati ).
A ni 7. zadatak, iako malo teži od 6., nije previše komplikovan. Ako na duži DA uočimo tačku E, tako da je DE=a, EA=b , pa konstruišemo duž CE, pojavljuju se tri jednakokraka trougla. Koristeći spoljašnje uglove trougla dobijamo da je mera nepoznatog ugla 20o. [ sikira069 @ 24.05.2024. 12:32 ] @
U 12-om zadatku je rešenje 2.880.
Od 5 nematematičkih knjiga biramo 3 koje umećemo između matematičkih. To je 5 nad 3 jednako 10. 10*3!*4!*2 daje 2.880. Tačno je ovo što je napisao X-files. Takva odeljenja 7-og i 8-og razreda postoje i u klasičnim gimnazijama van Beograda. Pripremaju se za upis SM odeljenja u gimnazijama. Nastava u SM odeljenjima se obavlja po programu MG. Znači deca su 7-mi i 8-mi razred, ali se nastava odvija u gimnaziji po posebnom programu. Oni bolji probaju da upišu i MG. Sad da li rade i kombinatoriku na visokom nivou ne znam. Ali geometriju i analizu rade vrlo ozbiljno. Oće neko da pokuša 10-ti zadatak? Ili da pišem rešenje. [Ovu poruku je menjao sikira069 dana 24.05.2024. u 14:06 GMT+1] [Ovu poruku je menjao sikira069 dana 24.05.2024. u 14:06 GMT+1] [ MajorFatal @ 24.05.2024. 13:26 ] @
Citat: djoka_l: 12. H - e tu sam baš bio u rebusu, dobio sam 1152, a to nije bilo ponuđeno. Računao sam, da bi knjige bile nesusedne, treba ih posaviti na parna mesta ili na neparna (1,3,5,7) ili (2,4,6,8). U stvari postoji 5 rasporeda, a ne dva (1,3,5,7), (1,3,5,8)(1,3,6,8), (1,4,6,8), (2,4,6,8). Na svakom od tih rasporeda knjige iz matematike se rasporede na 4! permutacija, a ostale knjige na 4!, pa je ukupan broj rasporeda 4!*4!*5 = 576*5 = 2880 Isto i još se čudim gde je među ponuđenim rezultat do koga sam došao, ali nisam uspeo da se setim da ima 5 rasporeda. Sad nešto gledam zadatak bi bio višestruko teži da je 1152 među ponuđenim odgovorima, ja bih to zaokružio iz prve bez mnogo razmišljanja. Ovako kad nema ćuška te da nađeš pravo rešenje. [ kosmopolita @ 24.05.2024. 15:30 ] @
Citat: Oće neko da pokuša 10-ti zadatak? Ili da pišem rešenje ] B 8 To sam dobio kucajući kod koji daje rešenje. [ mjanjic @ 24.05.2024. 16:06 ] @
Citat: X Files: Pre 10-tak godina, bio sam prilicno verziran za resavanje zadataka ovog nivoa, jer sam klinca spremao za neka takmicenja. Pokusao sam da i sam uradim tih 12 zadataka u zadatom roku, i ne secam se da sam ikada uspeo da uradim sve bez greske. Obrni okreni, makar 2 sam zasrao. Ja pre nekoliko godina na provokacije kolege svake godine da rešava prijemni na ETF-u skinem zadatke i prvih 10 uradim napamet, nakon čega sam ostavio test zbog drugih obaveza i setio se 2-3 dana kasnije, uradio sve preostale zadatke, osim jednog kod koga sam rešenje pogodio nakon nekoliko koraka rešavanja, posle čega se videlo unutar kog intervala mora biti, a samo jedno od ponuđenih rešenja je bilo u tom intervalu - kolega taj zadatak nije uradio :) Zadaci sa prijemnog na ETF-u su takvi da se često mogu uraditi u nekoliko koraka ili čak napamet, složeniji zadaci su druga priča, ali za nijedan ne treba više od pola a4 stranice. Međutim, većina srednjoškolaca nema razvijenu logiku i iskustvo da tako razmišlja, a tu retko pomaže i plaćanje privatnih časova, već uglavnom pomogne to što urade 1000 takvih zadataka i što im taj ko dugo godina drži privatne časove baš za takve prijemne ispite nauči decu trikovima kako se isti rešavaju. A poenta srednje škole bi trebala da bude da deca sama dođu do najboljeg i najbržeg načina za rešavanje nekih problema. Kao u šahu, ima onih koji mogu da zapamte na hiljade kombinacija, na desetine različitih otvaranja, a kada se nađu u nepoznatoj poziciji, totalno se pogube i naprave početničke greške. Zato, na žalost, imamo i onih koji završe taj ETF, a nisu ni blizu inženjeri kakvi bi trebali da budu u skladu sa renomeom diplome koju dobiju, ali šta tek reći za one koji završe daleko lakše fakultete. [ kosmopolita @ 24.05.2024. 16:25 ] @
Kaze da deca sada uce rešavanje zadataka i pobedjuju na takmičenjima.
Kad treba kasnije nesto konkretno da urade nema rezultata.. [ djoka_l @ 24.05.2024. 16:41 ] @
Citat: kosmopolita: Citat: Oće neko da pokuša 10-ti zadatak? Ili da pišem rešenje ] B 8 To sam dobio kucajući kod koji daje rešenje. Hm, pa i ja sam rešio, ali na prljav način. Pošto su ona prva tri izraza "simetrična", rekoh, pa što ne bi bilo x=y=z=a Kada zamenim x,y,z sa a, dobijem 1=1=1, pa (x,y,z) = (a,a,a) a<> 0 pripada skupu rešenja. Onda je onaj krajnji izraz 8a^3/a^3 = 8 E, sada, da li je moj postupak u redu za opšti slučaj, možda nije ni bitno, ako već treba da se samo zaokruži tačno rešenje, a postupak nije tačan. [ mjanjic @ 24.05.2024. 17:24 ] @
Da, kod ovakih testova je bitno zaokružiti tačno rešenje, a posebno je lagano ako je samo jedno od ponuđenih rešenja tačno i nije u pitanju interval i slično, već konkretna vrednost. Ovde je dovoljno probati šta se dešava ako je x=y=z=1, čime se dobija da je 8 vrednost datog izraza. Ko nije siguran da li to uvek važi za dati uslov, može da proba još i za x=y=z=2, mada se lako pokaže da važi ne samo za svaki broj iz skupa realnih, već i svaki broj iz skupa kompleksnih brojeva. Tu bi možda neki pogrešili kad bi se tražilo pod kojim uslovima za navedene jednakosti dati izraz ima neku vrednost i koja je to vrednost.
[ nato_bot @ 25.05.2024. 04:39 ] @
Citat: @sikira069 U 12-om zadatku je rešenje 2.880. Od 5 nematematičkih knjiga biramo 3 koje umećemo između matematičkih. To je 5 nad 3 jednako 10. 10*3!*4!*2 daje 2.880. Hm, dobio si tačno rešenje polazeći od netačnog stava da ima "5 nematematičkih knjiga". Završavam (običnu) osnovnu školu a na matematičkoj sekciji sam načuo za permutacije. Spremam se da prodjem taj ispit i pokušaću da rešim zadatak na sledeći način: Označimo skup (sada vec pocepanih) knjiga X={1,2,3,4,A,B,C,D} gde cifre 1,2,3,4 predstavljaju matematičke knjige. Rasporedimo nematematičke knjige a to je 4! = 24 načina. Cifre 1,2,3,4 se mogu rasporediti na krajevima i izmedju A i B, B i C, C i D. Ispišemo sve te načine gde # označava nematematičku knjigu: 1#2#3#4# #1#2#3#4 1##2#3#4 1#2##3#4 1#2#3##4 1#2#4#3# #1#2#4#3 1##2#4#3 1#2##4#3 1#2#4##3 1#3#2#4# #1#3#2#4 1##3#2#4 1#2##2#4 1#2#2##4 1#3#4#2# #1#3#4#2 1##3#4#2 1#2##4#2 1#2#4##2 1#4#2#3# #1#4#2#3 1##4#2#3 1#2##2#3 1#2#2##3 1#4#3#2# #1#4#3#2 1##4#3#2 1#2##3#2 1#2#3##2 Ukupno 30 načina ako je knjiga "1" na prvom mestu. Ovde stanem jer primetim da je analogno ako je 2,3,4 na prvom mestu. Tj 4*30 = 120 načina. Konačno 24*120 = 2880. [ nato_bot @ 25.05.2024. 06:04 ] @
Za 10. zadatak treba primetidi da izraz (2*y-z)/x == (2*z-x)/y == (2*x-y)/z
mora važiti i za x = y = z = a != 0. Tada je (x+y)*(y+z)*(z+x)/(x*y*z) = (a+a)*(a+a)*(a+a)/(a*a*a) = 8 [ sikira069 @ 25.05.2024. 10:41 ] @
Lapsus.
Trebalo je da piše od 5 pozicija za nematemstičke knjige. Probaj da uradiš zadatak sa 5 knjiga iz matematike i 7 koje nisu iz matematike? Ispisivanje rasporeda ne vodi ničemu u realnom vremenu. Jasno da zadatak nije za nivo đaka osmaka. [ jans @ 25.05.2024. 23:56 ] @
Još malo o 12-tom zadatku.
Mislim da 12. zadatak mogu da reše učenici 8. razreda. nato_bot ga je rešio ali njegov postupak, kao što je i sikira069 sugerisao, nije podesan ako je broj knjiga veći. Kao argument nato_botu predlažem da reši zadatak sa 5+5 ( ili 6+6 ) knjiga. Zadatak koji predlaže sikira069 ( sa 5+7 knjiga ) nije u kategoriji sa 12-tim zadatkom. Teži je, zato što je broj nematematičkih knjiga veći od broja matematičkih, pa u njegovom rešavanju možda treba koristiti binomne koeficijente, odnosno kombinacije, a to se uči u 4. gimnazije. Da bi rešili 12. zadatak učenici uopšte ne moraju da znaju šta su permutacije, varijacije i kombinacije, niti da znaju faktorijel i binomne koeficijente. Dovoljno je da znaju pravilo množenja. ( U prvom ozbiljnijem susretu sa kombinatorikom, a to je u višim razredima OŠ na vannastavnim aktivnostima, odnosno u 1. razredu gimnazije i nekih stručnih škola kroz redovnu nastavu, učenici treba da nauče dva osnovna pravila kombinatorike – Pravilo proizvoda i Pravilo zbira, eventualno i faktorijel, radi kraćeg zapisivanja. A definicije permutacija,.. i formule tek u 4. gimnazije. ) djoka_I je primenio postupak baziran na tom pravilu. I još molba za člana sikira069. Ne znam kako drugi, ali ja, iako sam uzeo u obzir lapsus koji si načinio, nisam razumeo tvoj postupak, pa ako bi mogao malo detaljnije. [ sikira069 @ 26.05.2024. 09:57 ] @
#1#2#3#4#
1, 2, 3 i 4 su knjige iz matematike. # su kandidati za mesta za knjige iz nematematike. Preko kombinacija sa ponavljanjem se dobije da na # nematematičke knjige možemo rasporediti na 5 načina. Uslov je bio da na drugu, treću i četvrtu # mora da se stavi knjiga. 5*(4!)*(4!) = 2880. Bez kombinacija sa ponavljanjem trebalo je ručno izbrojati broj rasporeda na # mestima, a to su sledećih 5: 01111 01120 01210 02110 11110 [Ovu poruku je menjao sikira069 dana 26.05.2024. u 13:49 GMT+1] [ nato_bot @ 28.05.2024. 02:46 ] @
Koja svrha da ispisujem ista rešenja kao i ostali?
Pokazao sam da se 12. zadatak može rešiti bez ikakve teorije, nije neophodno ni pravilo zbira ni pravilo proizvoda ni faktorijel koji vi ispisujete. Dovoljno je da učenik malo više radi i da ume da "ispremešta" elemente. [ kosmopolita @ 28.05.2024. 07:39 ] @
Matematika bi trebala da bude jasna i nedvosmislena.
Ako matematika moze da bude relativizovana onda politika nema sanse nikakve. [ nato_bot @ 28.05.2024. 10:42 ] @
Citat: sikira069 Probaj da uradiš zadatak sa 5 knjiga iz matematike i 7 koje nisu iz matematike? Nisi ponudio odgovore :) [ test1234 @ 05.06.2024. 19:43 ] @
Nije baš mnogo vezano za ovu temu ali možda je interesantno.
U zadnje dve godine česte mušterije su mi Rusi i to redovno porodice sa dvoje troje dece. I nezaobilazno pitanje moje deci je koja razlika je u školi. Svi listom govore da se u Rusiji mnogo više uči matematika i fizika plus da je disciplina na mnogo većem nivou, u Rusiji. Klinci oduševljeni druženjem i zezenjem. [ sikira069 @ 07.06.2024. 05:02 ] @
Citat: nato_bot: Citat: sikira069 Probaj da uradiš zadatak sa 5 knjiga iz matematike i 7 koje nisu iz matematike? Nisi ponudio odgovore :) Preko kombinacija sa ponavljanjem neđemo da ima 56 rasporeda za knjige iz nematematike. Rešenje je: 56*(7!)*(5!). [ test1234 @ 12.06.2024. 05:52 ] @
Pošto je diskusija zamrla evo rešenja…
https://ceo.edu.rs/wp-content/...ni_MAT_mat-gimnazija_Kljuc.pdf [ mjanjic @ 13.06.2024. 09:23 ] @
Zanimljivo bi bilo da znamo MD5 heš (5b17d65cb399de467d081a20683b52c9), kao i da je dobijen od niza karaktera koji su tačni odgovori na zadatke sa testa (npr. ACGBCGH...), a zadatak je naći ulazni string od tih 12 karaktera ;)
Pošto se koristi samo 8 karaktera (slova A-H), nema mnogo kombinacija za ispitivanje - 68,719,476,736 :) Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|