|
|
[ miki069 @ 27.11.2024. 09:10 ] @
|
| http://e.math.hr/math_e_articl...vcic_skrtic_pavrlisak/bertrand
U sva tri rešenja jeste pokrivena cela površina kruga, ali nisu generisane sve tetive.
Sve tetive se generišu slučajnim izborom dve tačke koje su krajevi tetive, a rasponu su od 0 do obima kruga.
Uz dati uslov lako se dobije da je verovatnoća 4/9.
Tako da, po meni, ovo i nije paradoks.
|
[ miki069 @ 28.11.2024. 07:20 ] @
Rešenje "paradoksa" je u prilogu.
[ MajorFatal @ 29.11.2024. 22:04 ] @
Mislim da se podrazumeva da na koji god način odabereš početnu tačku, na taj isti način možeš da odabereš koliko god hoćeš tački, što na kružnici, radijusu, unutar kružnice, princip je isti, i uvek se dobija isti rezultat ..
Nisam baš sve najbolje razumeo, ali ja bih možda imao drugačiju primedbu: rešenje iz prvog primera 1/3 mislim da nije tačno .. u zadatku, paradoksu, se traže tetive koje su >>veće<< od stranice trougla, da se traže koje su >>veće ili jednake<< možda bi rešenje bilo 1/3, dužina luka UV jeste jednaka trećini opsega kružnice, ali uključujući tačke U i V u tu trećinu, tu postoje dve tetive koje nisu ni veće ni manje od dužine stranice trougla, nego su jednake dužini stranice trougla, a to su tetive TV i TU, tako da bi rešenje trebalo biti 1/3 -2, i tu onda možda možeš da vidiš u čemu se satoji paradoks, a to je u klimavo definisanim uslovima, 1/3 čega minus 2, nedostaje jedinica mere, koja doduše u matematici nije neophodna, ali kao i dosta paradoksa ovaj bludi negde između matematike i fizike, trebalo bi 1/3 od beskonačno mnogo tetiva koje možeš da provučeš kroz tačku T i luk UV, minus dve tetive koje su jednake stranici trougla ... ako se nisam baš mnogo iznalupetao .. :)
Citat: Sve tetive se generišu slučajnim izborom dve tačke koje su krajevi tetive, a rasponu su od 0 do obima kruga.
Uz dati uslov lako se dobije da je verovatnoća 4/9.
Šta ako odaberem za x tačku 1/37 x Pi x r, i za y isto 1/37 x Pi x r, nisam ni dobio tetivu nego tačku, da računam da je tačka kraća od stranice trougla ili kako?
Citat: Tako da, po meni, ovo i nije paradoks.
Tjah .. što se tiče "fizičkih" dokaza da paradoks radi, šta ako se pojavi neko ko non stop gađa liniju upisane kružnice strelicom za pikado u trećem primeru, ili ne mora non stop, nego sa određenim procentom, da li su te tetive kraće ili duže, ili jednake stranici trougla itd itd ...
[ djoka_l @ 29.11.2024. 23:09 ] @
Citat: Nisam baš sve najbolje razumeo, ali ja bih možda imao drugačiju primedbu: rešenje iz prvog primera 1/3 mislim da nije tačno .. u zadatku, paradoksu, se traže tetive koje su >>veće<< od stranice trougla, da se traže koje su >>veće ili jednake<< možda bi rešenje bilo 1/3, dužina luka UV jeste jednaka trećini opsega kružnice, ali uključujući tačke U i V u tu trećinu, tu postoje dve tetive koje nisu ni veće ni manje od dužine stranice trougla, nego su jednake dužini stranice trougla, a to su tetive TV i TU, tako da bi rešenje trebalo biti 1/3 -2, i tu onda možda možeš da vidiš u čemu se satoji paradoks, a to je u klimavo definisanim uslovima, 1/3 čega minus 2, nedostaje jedinica mere, koja doduše u matematici nije neophodna, ali kao i dosta paradoksa ovaj bludi negde između matematike i fizike, trebalo bi 1/3 od beskonačno mnogo tetiva koje možeš da provučeš kroz tačku T i luk UV, minus dve tetive koje su jednake stranici trougla ... ako se nisam baš mnogo iznalupetao .. :)
Jesi se izlupetao. Postoji beskonačno mnogo tetiva u prvoj postavci zadatka (a i u ostalim). To što postoje dve tetive koje su jednake ne menja rezultat jer je beskonačno - 2 i dalje beskonačno.
Porede se dve beskonačnosti, a to je broj tačaka na luku u odnosu na broj tačaka na kružnici, a to je jedna trećina. [ MajorFatal @ 30.11.2024. 00:06 ] @
Prema tome da su se u postavci zadatka paradoksa tražile tetive koje su "veće ili jednake" stranici, rešenje bi isto bilo 1/3 ?
[ djoka_l @ 30.11.2024. 00:38 ] @
Tako je https://e-statistika.rs/neprekidna-slucajna-promenljiva
Kada imas raspodelu koja je neprekidna funkcija na nekom opsegu, ne racunas tako sto prebrojavas moguce vrednosti, nego racunas integral.
Opseg u kome se nalaze moguce vrednosti za poziciju tacke je integral ugla u slucaju ovog zadatka. Dakle ceo opseg je od 0 do 2pi, a opseg u kojem je vrednost veca je 2pi/3 do 4pi/3
Svejedno je da li je taj opseg (2pi/3, 4pi/3) ili [2pi/3, 4pi/3] - bez obzira da li si uzeo krajnje tacke ili ne u integral, on je isti - 2pi/3
U stvari, verovatnoca da je duzina tangente jednaka stranici je nula. Kao i da je jednaka bilo kojoj drugoj vrednosti. Nije definisana.
Ali moze da se odredi verovatnoca da je slucajna promenljiva u nekom opsegu. [ MajorFatal @ 30.11.2024. 11:05 ] @
Isuviše komplikovano za mene .. nego je zadatak stajao tri dana pa reko da reknem bar nešto ..
"U stvari, verovatnoca da je duzina tangente jednaka stranici je nula. Kao i da je jednaka bilo kojoj drugoj vrednosti. Nije definisana.
Ali moze da se odredi verovatnoca da je slucajna promenljiva u nekom opsegu."
Je l onda mogu da izmišljam sledeći paradoks: Pošto je verovatnoća da je tangenta jednaka bilo kojoj od vrednosti od 0 do R jednaka nuli, onda je rešenje zadatka nula?
[ djoka_l @ 30.11.2024. 11:24 ] @
Zamisli sledeci slucaj.
Imas kocku. Verovatnoca da ce da izadje neki broj je 1/6
Povecaj broj stranica, pa sa svakim brojem stranica smanjuje se verovatnoca da ce se dobiti neki specificni ishod - 1/7, 1/8, ... 1/50...
Sta se desava ako je broj "stranica" beskonacan? To vise nije kocka nego sfera. Verovatnoca da neka secificna tacka bude u kontaktu sa stolom je 1/beskonacno, odnosno 0.
E sada zamisli da je ta sfera obojena pola u plavo, pola u crveno. Koja je verovatnoca da plava tacka bude oslonjena o sto? Naravno 50%
Dakle iako je verovatnoca da bio koja specificna tacka bude u kontaktu sa stolom 0, mnogo tih beskonacno malih veovatnoca daju konkretan procenat.
To je sve verovatno malo novo u matematici, nema ni 400 godina kako su Njutn i Lajbnic to postavili.
[ MajorFatal @ 30.11.2024. 12:13 ] @
Kad tako objasniš, takoreći ilustruješ, zaista je mnogo jasnije, hvala.
Ma kakav Lajbnic, kad je išta uradio mimo Njutna, nikad ništa ..
[ MajorFatal @ 01.12.2024. 15:36 ] @
A što se tiče pitanja iz naslova, da li je paradoks ili nije ...
Bertrandov paradoks je problem iz vjerojatnosti, koji je francuski matematičar Joseph Bertrand (1822. – 1900.) predstavio u svom djelu Calcul des probabilités (1888.) kao primjer koji pokazuje da vjerojatnosti ne moraju biti dobro određene ako metoda kojom generiramo slučajnu varijablu nije jasno zadana.
Ako si se odlučio za metodu kojom generišeš slučajnu varijablu koja je "jasno zadana" onda to ne spada u opis paradoksalnog dela određivanja verovatnoća, one važe samo ako metoda nije jasno zadata :)
Takođe bilo bi kul da možeš da smisliš fizički eksperiment koji pokazuje da je tvoje rešenje tačno, možda da jedanput zavrtiš kazaljke, drugi put bacaš slamke, i treći put pikado, i tako naizmenično, mnogo puta .. ako pokaže 4/9 tvoje rešenje je tačno ...
[ miki069 @ 03.12.2024. 12:51 ] @
Zadatak je da se izegenerišu sve tetive, a ne samo da se pokrije cela površina kruga.
Fizički model bi bio bacanje štapa na krug, pa merenje dužine tetive.
U datom rešenju nedostaje uslov abs(y-x)<4*pi/3. Sa tim uslovom verovatnoća se menja u 33.33%.
Napisao sam programče koje random gađa dve tačke u krugu, pa jednačina prave kroz te dve tačke i onda presek sa kružnicom, pa dužina tetive.
Verovatnoća kovergira ka 21.7%.
Idealno bi bilo da biram tačke na kružnici, ali je Đoka objasnio da verovatnoća da odabrana tačka bude na kružnici je nula.
Mislim da je i izbor 2 tačke u krugu verna simulacija slučajne tetive.
Zbunjuje me rezultat od 21.7%.
Ako treba okačiću programče.
[ MajorFatal @ 03.12.2024. 22:04 ] @
Citat: miki069: Zadatak je da se izegenerišu sve tetive, a ne samo da se pokrije cela površina kruga.
Ali on jeste izgenerisao sve tetive, to što je na ilustraciji samo jedan primer, sa samo jednom, ili dve tačke, u zavisnosti od metoda, važi i za sve ostale slučajeve slučajnog biranja tačke na kružnici ili unutar .. kao na slici ..
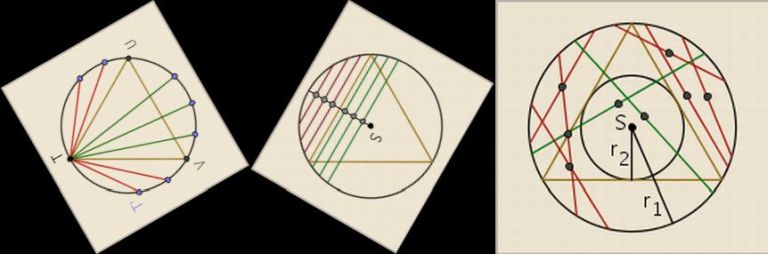
Citat: Fizički model bi bio bacanje štapa na krug, pa merenje dužine tetive.
To već ima kod njega, on je to ilustrovao kao "bacanje slamčice na krug", a rezultat takvog eksperimenta je uvek 1/2
Citat: Napisao sam programče koje random gađa dve tačke u krugu, pa jednačina prave kroz te dve tačke i onda presek sa kružnicom, pa dužina tetive.
Verovatnoća kovergira ka 21.7%. Zbunjuje me rezultat od 21.7%.
Ha! A mene izgleda ne, u stvari tvoj rezultat je 1/5 nastavak progresije koju je on našao, onih 1,7% viška je bag softvera koji glumi random generator slučajnih brojeva. A evo i kako i zašto izgleda, njegova progresija je biranje jedne tačke na kružnici - rezultat 1/2, dve tačke na kružnici - rezultat 1/3, jedna tačka unutar kružnice - rezultat 1/4, ... ti si se odlučio za biranje dve tačke unutar kružnice, rezultat je 1/5 ... čak sam smislio i fizički eksperiment koji će da pokaže naočigled da si bespogovorno u pravu .. ti bi mogao da bacaš na tablu za pikado onu špaknu za prevrtanje roštilj mesa i šnicli, zašto .. pa zato što ima dva šiljka koji će da simuliraju biranje dve tačke unutar kružnice, zašto se verovatnoća prividno redukuje na 1/5 pa zato što zahvaljući djoki_I i ostalim ljubiteljima roštilj mesa svi znamo da strelica za pikado ima tendenciju baš da pogodi pravo na liniju između 2 broja, i onda se igrači posvađaju i prekine turnir, pa su onda izmislili onu tablu sa metalnom rešetkom baš preko linija, pa onu drugu sa rupicama predviđenim za strelice i elektronskim brojanjem itd .. mislim da se verovatnoća redukuje pri svakom sledećem koraku, matematički, i prividno fizički, zato što se odbacuju svi rezultati gde je 1. slamčica pala tako da dotiče liniju kruga 2. obe skazaljke se poklopile pa dobio jednu tačku 3. pikado pogodio baš na liniju, bilo spoljnu kruga, bilo unutrašnjeg kruga koji služi za određivanje da li je tetiva duža ili ne ... u tvom slučaju tetiva je duža ako je bar jedan šiljak unutar unutrašnjeg kruga, ili ako su oba unutar, a kraća ako su oba u spoljnjem krugu, a odbacivali bi se svi rezultati kad je viljuška pogodila bar jednim šiljkom, ili sa oba, spoljašnji krug, ili unutrašnju kružnicu ... sve te situacije se u fizičkom eksperimentu ne broje, a viljuška dobro pokazuje verovatnoću 1/5.
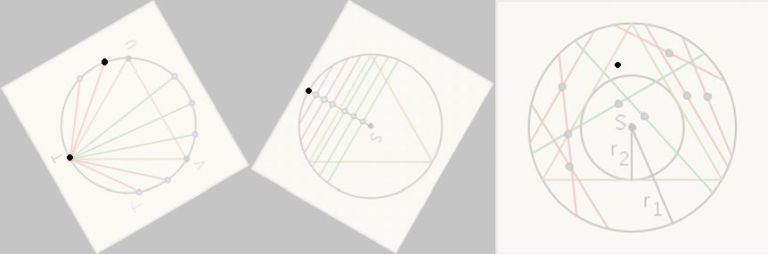
Slika je ilustracija da se odlučio za biranje jedne tačke na kružnici, dve tačke na kružnici, i jednu tačku unutar kružnice .. ti si se odlučio za dve tačke unutar kružnice.

Način na koji špakna bira dve tačke ...
Citat: Idealno bi bilo da biram tačke na kružnici, ali je Đoka objasnio da verovatnoća da odabrana tačka bude na kružnici je nula.
Ma kakav djoka on loše objašnjava, naravno da može da bude tačka na kružnici još od prva dva primera dve skazaljke, i slamčice ... još malo da objasnimo i da nas upisuju u panteon matematike ..
Citat: Mislim da je i izbor 2 tačke u krugu verna simulacija slučajne tetive.
Naravno, ali i sve prethodne su, biranje jedne i dve tačke na kružnici, i biranje jedne tačke unutar kružnice i proglašavanje nje za sredinu tetive ...
Citat: U datom rešenju nedostaje uslov abs(y-x)<4*pi/3. Sa tim uslovom verovatnoća se menja u 33.33%.
E sad se ja nerviram što ne umem da objasnim jer sam se pogubio u ovim abs, x, y, Pi/3 itd, a dodatno nervira što je rezultat tačno poklapanje sa 1/3 tj. 33,33%, pa onih 1,7% viška ili greške kod biranja dve tačke verovatno potiče od toga što je tvoja softverska "viljuška" varijabilna, čas je uža čas šira u zavisnosti od dve odabrane tačke ... trebalo bi da se smisli grafičko, geometrijsko rešenje gde se krug gađa sa kratkim dužima, i ista takva interpretacija bilo sa rotiranjem unutrašnjeg trougla, bilo sa onom unutrašnjom kružnicom i površinama ... Ah da propustio sam da prebrojim situaciju kad je viljuška pala jako blizu linije unutrašnje kružnice a izvan nje, ali tako da su oba šiljka toliko blizu da tetiva provučena kroz njih prolazi kroz unutrašnju kružnicu, viljuška je izvan, ali je tetiva duža od stranice trougla! Tu se krije onih 1,7% viška! [ MajorFatal @ 04.12.2024. 07:06 ] @
Uh, mora jedna ispravka, špakna sa dva šiljka će da definiše tangentu dužu od stranice trougla čak i ako cela, tj. oba šiljka padnu izvan manje kružnice, pod uslovom da pravac tangente koji na taj način određuje prolazi kroz manju, centralnu kružnicu .. i dodatni uslov da je sama špakna, tj. razmak između 2 šiljka manji od r2 jer to je ujedno i razmak između manje centralne i veće kružnice koja obuhvata celu konstrukciju.
Do razlike u rezultatima dolazi jer poredi različite površine kruga, a tvrdi da je svaki put povukao beskonačno mnogo tangenti kroz te različite površine, dokaz je to što je i u drugom eksperimentu mogao da zavrti kazaljku, dobio bi jednu tačku na kružnici u svakom slučaju. I obrnuto: u prvom eksperimentu mogao je da baci štap, ili slamčicu, dobio bi obe tačke odjednom, bez da vrti kazaljke, al se onda rezultati ne bi slagali, te paradoks ne bi bio lep. U trećem eksperimentu možeš bacati pikado koliko god hoćeš, kad je površina unutrašnje kružnice 1/4 rezultat će uvek biti 1/4 ...
[ miki069 @ 04.12.2024. 11:27 ] @
Revidiram stav. Programče koje bira dve tačke unutar kruga je beskorisna masa, jer za datu tetivu postoji beskonačno tačaka na datoj tetivu koje generišu istu. Rešenje je 1/3. Okačiću sliku sa ispravnim rešenjem. Paradoks ne postoji.
Napisaću i programče koje bira dve tačke na kružnici.
Samo će to mnogo sporo da radi.
[Ovu poruku je menjao miki069 dana 04.12.2024. u 12:50 GMT+1]
[ miki069 @ 04.12.2024. 12:14 ] @
U Dekartovim pravouglim koordinatama sporo. U polarnim koordinatama će da radi mnogo brzo. Kad završim šaljem rezultat.
[ MajorFatal @ 04.12.2024. 23:54 ] @
Citat: miki069:
Revidiram stav. Programče koje bira dve tačke unutar kruga je beskorisna masa, jer za datu tetivu postoji beskonačno tačaka na datoj tetivu koje generišu istu.
Pa i kad odabereš dve krajnje tačke tetive na kružnici, isto će da postoji beskonačno mnogo tačaka na samoj tetivi koje mogu da je generišu? :)
Citat: Rešenje je 1/3. Okačiću sliku sa ispravnim rešenjem. Paradoks ne postoji.
Napisaću i programče koje bira dve tačke na kružnici.
Samo će to mnogo sporo da radi.
Ta i Bertrand je rekao da je rešenje 1/3 ako biraš dve tačke na kružnici, a ti upravo to sad radiš softverski. Ja se nadam da paradoks postoji, i da si ga ti proširio na još jedan rezultat, a to je 1/5 ako se biraju dve tačke unutar kružnice .. i hoću da pokažem zašto će roštiljska špakna savršeno da imitira da je ta verovatnoća baš ta, i da je to fizički eksperiment koji to dokazuje, a delimično i jeste. Špakna kad se zabode u pikado tablu označi dve tačke, ali samim tim definiše i liniju između njih, koja opet pokazuje orijentaciju tangente. U principu površina spoljašnjeg prstena pikado table je tri puta veća od površine unutrašnje kružnice, pa špakna ima tri puta više mesta gde da padne na prsten, a verovatnoća da će pasti unutar unutrašnje kružnice je 1/4 .. međutim, i špakne koje padnu izvan unutrašnje kružnice mogu da budu orijentisane tako da prolaze kroz kružnicu, pa bi sve ukupno tu verovatnoća bila 1/2 ...
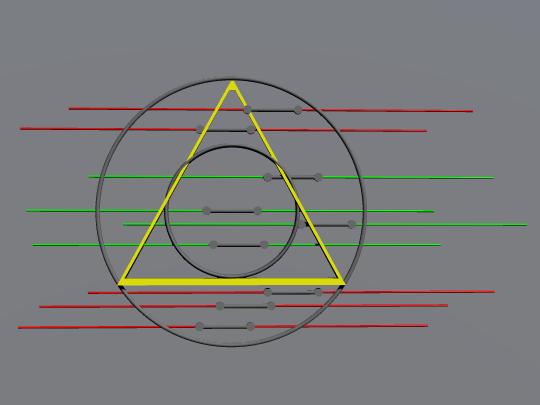
Međutim špakne mogu da budu različito orijentisane, za one koje padaju unutar unutrašnje kružnice, a koja je 1/4 površine celog kruga nije bitno, jer su sve duže od linije trougla. Tri puta više špakni će pasti na prsten koji je površinom veći, a one mogu biti različito orijentisane, samo će neki uzan snop gađati u pravcu unutrašnje kružnice, ostale će je mašiti, na ilustraciji jedna od četri je duža od linije trougla, ovo će da redukuje verovatnoću sa 1/2 na .. 1/5 na primer ..
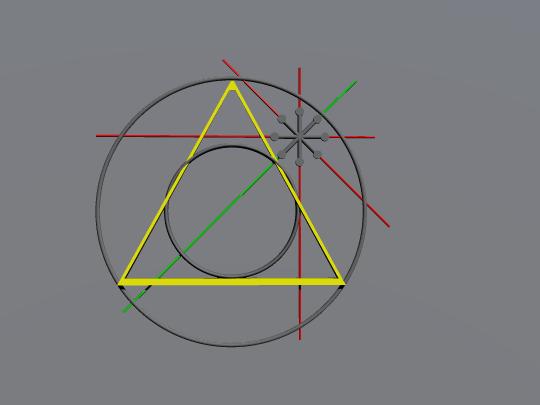
I na kraju situacija kad špakna pogodi jako blizu unutrašnje kružnice, izvan, ali sa oba šiljka toliko blizu da linija koju definišu prolazi kroz kružnicu, i ta tangenta će biti duža od linije trougla, i to će dodati 1,7% na prethodnih 20% za sve ukupno 21,7% Tjah .. eo ne znam, moglo bi biti ..
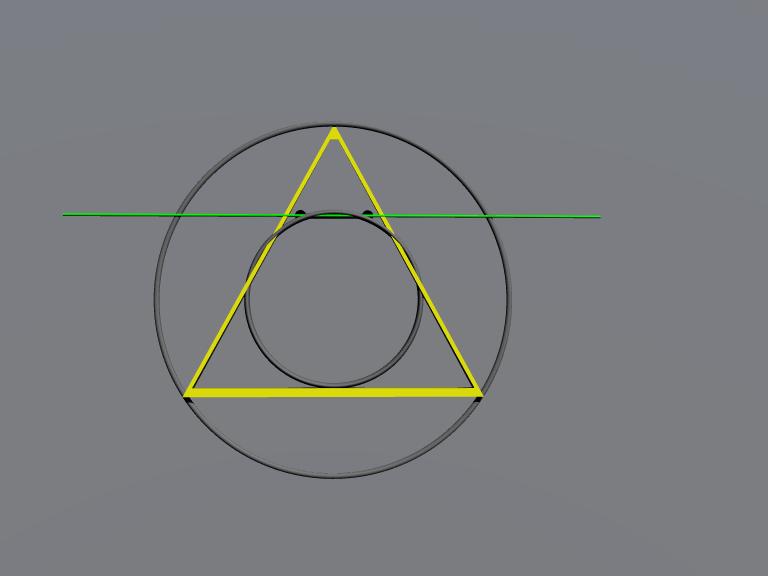 [ miki069 @ 05.12.2024. 00:13 ] @
Gospodine Majore, sutra (danas) ću se obratiti javnosti.
Radi se o generisanju svih tetiva, a ne o pokrivanju kruga tetivama.
[ miki069 @ 05.12.2024. 11:18 ] @
Posle generisanja svih tetiva, rezultat je 1/3.
Paradoks ne postoji.
[ MajorFatal @ 05.12.2024. 22:57 ] @
Odabereš slučajnim načinom tačku t1 na kružnici, generišeš sve tetive u tom pravcu, svih dužina, neke su duže od linije trougla, neke kraće, odnos je 1/2 ... Odabereš slučajnom metodom sledeću tačku na kružnici t2, generišeš sve tetive u tom pravcu ... i tako u krug oko cele kružnice, postoji beskonačan broj tačaka .. ti to nazivaš "prekrivanje kruga tetivama" a meni se čini da je on generisao sve moguće tetive, svih dužina, iz svih pravaca, kojih ima beskonačno mnogo, a sve to ilustrovao sa pola kružnice pokriveno tetivama (jer je i drugo pola kružnice isto, identične su) i jednom tačkom primera radi ... meni njegovo rešenje deluje i bolje jer je geometrijsko, i jer se beskonačno podrazumeva ..
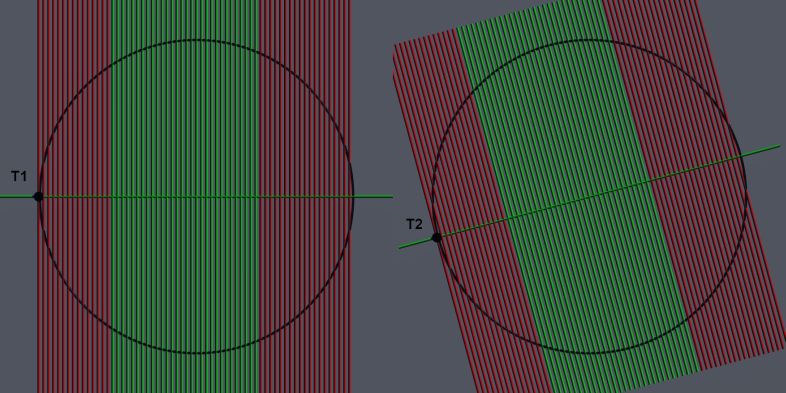 [ miki069 @ 06.12.2024. 09:18 ] @
Bravo Majore. Vrlo dobro Majore.
Bertran je tako iskazao prvo rešenje, koje je jedino ispravno i daje 1/3.
Ali nije pokazao ovo što si ti pokazao u predhodnom postu.
Dali nije razumeo problem ili se pravio naivan, da bi otvorio paradoks.
Njegova druga dva rešenja su neispravna.
Prilažem konačno rešenje, koje se uklapa sa tvojim.
Kolega Jans mi je na jednom drugom forumu ispravio neispravno rešenje koje sam bio okačio.
Veliko hvala i kolegi Jansu.
[ MajorFatal @ 06.12.2024. 19:18 ] @
Citat: miki069:
Bertran je tako iskazao prvo rešenje, koje je jedino ispravno i daje 1/3.
Pa i nije :) Nekad se baš loše razumemo, ja sam nacrtao njegovo rešenje broj dva, samo sam proširio na celu kružnicu, i naveo primer dve tačke kad se biraju jedna pa druga koje sve tetive mogu da se konstruišu, a u oba slučaja u pitanju je beskonačan broj tetiva, 1/2 je kraćih a 1/2 dužih od stranice trougla, dokazano geometrijski.
Citat: Njegova druga dva rešenja su neispravna.
Eh pa to bi već morao da dokazuješ, pokažeš, objasniš zašto misliš da su druga dva rešenja netačna, a postoje čak i fizički eksperimenti koji ih potvrđuju.
Citat: Prilažem konačno rešenje, koje se uklapa sa tvojim.
Kolega Jans mi je na jednom drugom forumu ispravio neispravno rešenje koje sam bio okačio.
Veliko hvala i kolegi Jansu.
Moj predlog je i dalje da paradoks postoji, a da si ga ti proširio sa još jednim postupkom, rezultatom, i fizičkim eksperimentom koji će da potvrdi taj rezultat ... taj postupak je biranje dve tačke unutar kružnice koje definišu tetivu, rezultat je 1/5, a fizički eksperiment gađanje pikado table špaknom, nožem, sekirom, satarom, bilo čime što će definisati dve tačke, a samim tim i pravac tangente ...
a umorio sam se od crtanja, pa ću sad samo nabrojati šta je sve Bertran uradio tokom izlaganja ovog paradoksa ... :
1. Mislim da je on pratio progresiju biram jednu tačku na kružnici, pa dve tačke na kružnici, pa tri tačke na kružnici, samo je taj poslednji primer tri tačke na kružnici zamaskirao kao jedna tačka unutar kružnice, nju bi dobio ako bi našao težište tri tačke na kružnici na primer.
2. Izmešao je redosled, umesto da rešenja predstavlja tako 1/2, pa 1/3, pa 1/4 odlučio se za 1/3, pa 1/2, pa 1/4 ...
3. U (svom) primeru broj dva koristio je paralelne tetive, u primeru broj jedan tetive koje se radijalno šire krećući iz jedne tačke na kružnici, i u primeru broj tri nasumične u svim pravcima, u sva tri primera broj tetiva je beskonačan, kao i broj početnih tačaka ili središnjih, na kružnici, ili unutar kružnice, ali sva rešenja su i važeća i tačna ako pitaš nekog ko se bavi geometrijom ...
4. Fizički eksperimenti su tek malo nategnuti, i deluje da je samo našao eksperimente koji imaju odgovarajuće rezultate, i jednostavno ih pridružio svojim geometrijskim rezultatima. Ne opisuju dosledno geometrijska rešenja.
4a. Problem je što se u primeru broj dva biranje jedne tačke na kružnici ne može postići bacanjem slamke ili štapa na kružnicu, jer se kad slamka ili štap preseku kružnicu dobija dve tačke odjednom, ali njemu je odgovarao rezultat 1/2 pa jednostavno pridružio. Biranje samo jedne tačke na kružnici se recimo može dobiti nasumičnim okretanjem jedne kazaljke .. Dodatni malo problem je kad imaš jednu tačku na kružnici red bi bio da odatle konstruišeš tetive, on radi nešto drugo, povuče prečnik pa bezbroj paralenih tetiva, ok
4b. ali zato u eksperimentu i rešenju broj jedan iako ima već dve tačke odabrane na kružnici, uz pomoć dve nasumično zavrćene kazaljke, jednu fiksira, i odatle povlači bezbroj radijalnih tetiva, i njih ima beskonačno, i svih dužina, itd, ali to baš i nije isto kao paralelne tetive, te to je mogao i samo sa jednom tačkom, kao što bi bilo vrćenje jedne kazaljke a ne dve ...
4c. je tek nategnut, biranje nasumične tačke unutar kružnice je ok birati pikadom, i određivanje da li je duža ili kraća na osnovu unutrašnje kružnice, ali proglašavanje za sredinu tetive donosi sledeću vrstu tetiva, nasumične, nit paralelne, nit radijalne .. Ako hoćeš da se baviš ovim paradoksom do sad imaš tri vrste biranja tačaka, i tri vrste (geometrijski predstavljenih) tetiva ..
5. Na sve to u dokazima uzima tri različita dela kružnice, u jednom slučaju četvrtinu kruga, u drugom slučaju trećinu luka, u trećem slučaju upisanu kružnicu .. ok mr Bertran .. da li je namerno? Verovatno dosta vremena proveo nad ovim, ali opet nije mogao sebi da objasni zašto dobija različite rezultate kad na različit način bira tačke ...
Tri vrste biranja tački, tri vrste tetiva, i tri različita dela kružnice za matricu 3x3x3 = 27 raznih tumačenja i objašnjavanja, svega ima beskonačno, a ipak sve može da se izrazi u merama, dužinama i površinama, pa ti raspetljavaj ako imaš vremena ..
Ja bih ti opet skrenuo pažnju da ti imaš nešto novo, proširenje paradoksa, nasumično biranje dve tačke unutar kružnice, koje savršeno mogu da opišu neku tetivu, odnosno sve, beskonačan broj tetiva koje se tako mogu odrediti, i rezultat 1/5 koji je nastavak progresije ..
[ MajorFatal @ 07.12.2024. 16:00 ] @
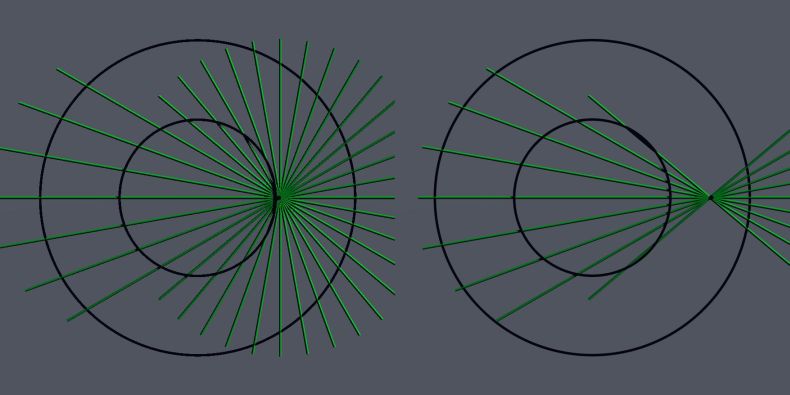
Nije me mrzelo da bar pokušam da proverim, našao sam ovu sliku na internetima, random crtice u krugu, samo sam dodao spoljnu i unutrašnju kružnicu i brojao .. špakni definisanih sa po dve tačke tj. linijica na crtežu ima sve ukupno 175, one koje su cele završile u unutrašnjem krugu njih ima 23 (svetlo zelena boja), još 26 (tamno zelena) ima koje su bar jednom tačkom završile u unutrašnjem krugu, sve ukupno 49. I još ima špakni koje su se orijentisale tako da bi tetiva prošla kroz krug 46 (svetlo plave na crtežu), ukupno 94. Preostalo je još 81 špakna koja je i izvan kruga i orijentisana tako da je tetiva kraća od stranice trougla, crne boje i njih nisam ni bojao ni produžavao ... Prema tome .. ništa se ne slaže :)
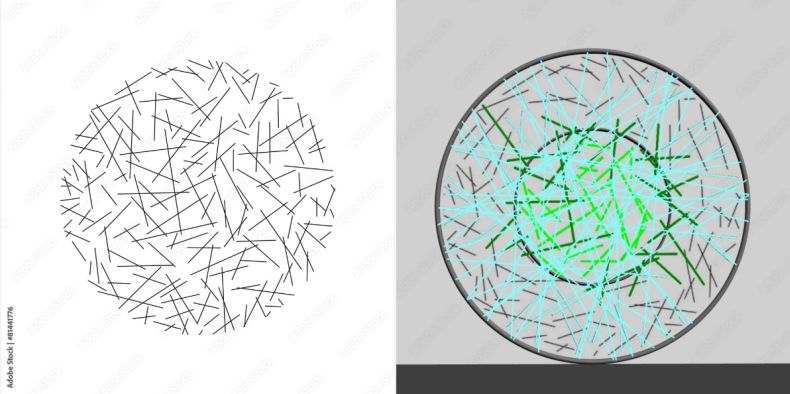 [ miki069 @ 07.12.2024. 16:28 ] @
Majore, imao sam grešku u programu.
Randomize funkcija u Pascalu ne greši.
Kada se biraju dve tačke unutar kruga verovatnoća je 75%, a ne 21%.
Nepravedno se favorizuju duže tetive.
Imaju mnogo veći raspon padanja ove tvoje naprave za roštilj.
Zadatak je kristalno jasan.
Sve tetive, a ne pokriti površinu kruga.
Krug se najlakše pokriva paralelnim tetivama, ali to nisu sve tetive.
[ MajorFatal @ 07.12.2024. 19:01 ] @
Ali sve paralelne, iz svih tački, to jest iz svih uglova, jesu sve tetive, svih dužina itd ..
Što se tiče randomize funkcije u paskalu tj. Delfiju, davno je bilo kad sam pravio igricu par - nepar, cimeri su bili spremni da se klade jer je bilo baš očigledno da više baca par nego nepar .. otprilike 5% više je izlazio par nego nepar ..
[ miki069 @ 08.12.2024. 05:19 ] @
Sve paralelne iz svih uglova, jesu sve tetive, ali u sva tri Bertranova rešenja toga nema.
Probaću par-nepar pa javljam.
Pravio sam za Yamb i bilo je 1/6 za svaki broj.
Najmanje 1.000.000.000 bacanja.
Ako si ti radio manje bacanja, u redu je da ode 5%
[ miki069 @ 09.12.2024. 08:16 ] @
Na 1.000.000.000 RND bacanja pismo pada u 50.00119% a glava u 49.99881%.
Na 100 000.000.000 RND bacanja pismo pada u 49.9998759% a glava u 50.0001241%.
[Ovu poruku je menjao miki069 dana 09.12.2024. u 12:34 GMT+1]
[ MajorFatal @ 09.12.2024. 16:21 ] @
Nemam pojma, smorih se, sad se nešto nosim mišlju da bi ne može špakna da odjednom odabere obe tačke i paradoks radi, kao što i slamka ili štap kad odrede obe tačke na kružnici odjednom verovatnoća je 1/2 ... nego .. da mora da se baca jedan pikado pa drugi unutar kružnice, znam da zvuči malo nelogično i da ne bi trebalo da ima veze, ali sve mi nešto padao na pamet onaj Montiholov paradoks, toliko je kontraintuitivan da su ljudi morali da otvaraju vrata i da se uvere gde je koza, bio na nekim kvizovima, proveravali ga u mitbastersima i uvek radi na čuđenje onih koji ne znaju matematiku i verovatnoću.
I onda se ispostavilo da je delimično povezan i sa drugim paradoksom tvog pulena - paradoks Bertrandove kutije ..
Kad prvo odabereš jednu tačku, verovatnoće za drugu tačku se malo promene .. ako pikado padne u centar, znači da će tetiva biti duža u svakom slučaju, ali verovatnoća da padne u centar je samo 1/4, mnogo veća verovatnoća je da će pasti negde na prsten 3/4 što će reći tri puta veća .. a ako padne na prsten blizu centra samo 1/2 sledećih gađanja odgovara, tj pod uglom max 180 stepeni prema centru .. ako padne dalje od centra blizu ivice same table ta verovatnoća se još redukuje, samo one pod uglom 60 stepeni na obe strane od centra će biti duže od stranice trougla ... i još nisam nacrtao sve, ako padne negde na sredinu između unutrašnje kružnice i ivice table odgovaraće uglovi koji zahvataju unutrašnju kružnicu i isvi oni kontra od njih na suprotnu stranu, jer će tetivu orijentisati tako da prolazi kroz unutrašnju kružnicu .. ma komplikovano ..
edit.. upravo uviden pogrešku .. ako prvi pikado padne jako blizu unutrašnje kružnice, ugao je 360 stepeni, tj svaki sledeći pogodak će da orijentiše tetivu da prolazi kroz manju kružnicu, kako se prvi pogodak pikada odmiče od centra ta verovatnoća se smanjuje na 1/6 tj samo pogodci obuhvaćeni uglom 60 stepeni prema manjoj kružnici odgovaraju .. mrzi me da crtam ispočetka .. pa evo prethodna ilustracija šta sam mislio ..
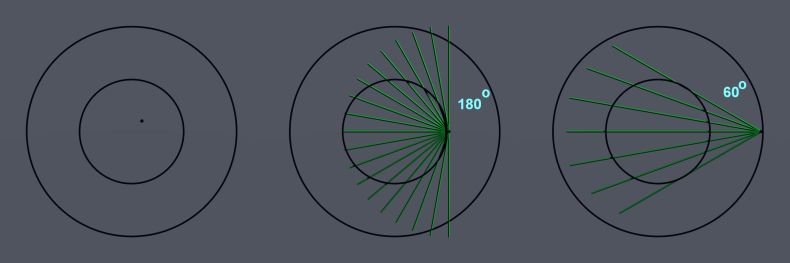 [ MajorFatal @ 09.12.2024. 16:38 ] @
Dakle ovako, na prethodnoj slici prva i treća su u redu, ali umesto druge bi išle ove dve, kad je prvi pogodak blizu unutrašnje kružnice, odgovara skoro svaki drugi, sem mali ugao pravo gore iznad prvog pogotka, i pravo dole ispod. Ako je prvi pogodak pikada na sredini prstena tetiva će biti duža samo ako sledeći pogodak padne negde u naspramnim uglovima levo prema unutrašnjoj kružnici i desno kontra od toga. I ja samo pominjem uglove, moraju da se računaju površine koje pokriva taj ugao na velikoj kružnici tj. tabli za pikado ..
A kad bude u kvizu, mora da se obrati pažnja na još jednu stvar, ljudi se trude da pogode centar table za pikado, zato takmičar mora da se okrene leđima i gađa tablu da bi dobio nasumične pogodke i pravilnu random distribuciju pogodaka po celoj tabli. Naravno da pazi da ne pogodi scenaristu ili reflektor .. :)
 [ miki069 @ 10.12.2024. 06:22 ] @
Majore kada se biraju dve tačke unutar kruga verovatnoća je 75%.
Što je i logično jer se forsiraju duže tetive.
[ MajorFatal @ 12.12.2024. 21:29 ] @
Tačke se biraju na slučajan način, šta je logično u tome da se na taj način forsiraju duže tetive? Trebalo bi i duže i kraće da se generišu podjednako?
[ miki069 @ 13.12.2024. 13:36 ] @
Duža tetiva ima "više" tačaka unutar kruga nego kraća tetiva.
Napisao sam pod znacima navoda jer se beskonačnosti ne upoređuju.
Više kombinacija po dve tačke unutar kruga generiše duže tetive, nego kraće.
Sa dva pikada, verovatnoća je 75%.
Ako hoćeš, priložiću program.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|









