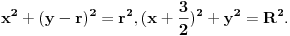|
|
[ MajorFatal @ 01.12.2024. 18:28 ] @
|
| Zadatak je gromoglasno najavljen kao "ako iko ikad reši" međutim pošto su neki ipak uspeli pojašnjeno je da je to zbog mesta postavljanja a to su društvene mreže, tako da ovde ne bi trebalo da ima većih problema ...
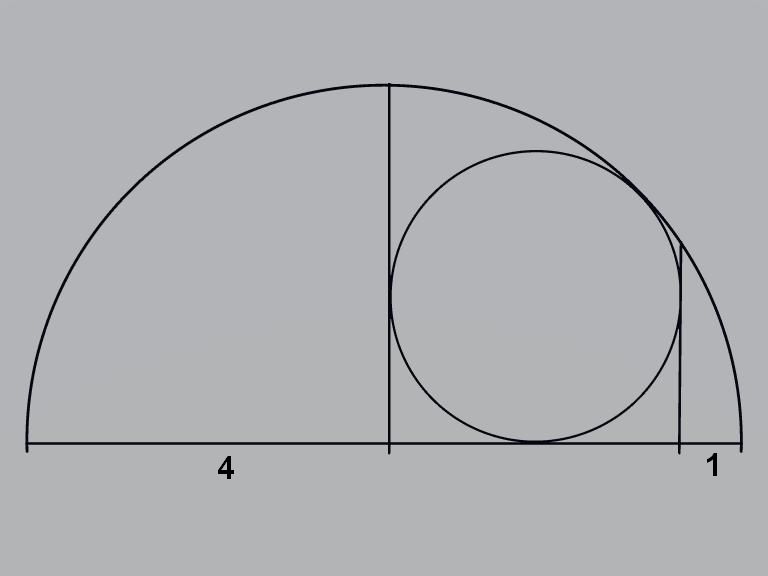
Ima pola kružnice, i unutar je upisana manja kružnica, povučene su dve normale na prečnik veće "polukružnice", manja kružnica dodiruje "sve oko sebe" tj tri duži i luk, normale na prečniku odsecaju delove čije su dužine 4 i 1, a pitanje koje se postavlja je: Koliki je poluprečnik manje, upisane kružnice?
 |
[ scoolptor @ 01.12.2024. 19:09 ] @
r=5/(2*sqrt(2))
[ MajorFatal @ 01.12.2024. 19:12 ] @
Teško da je to rezultat tačan rezultat .. mslm nije.
[ scoolptor @ 01.12.2024. 19:20 ] @
Da, da. Vidim gde sam pogresio.
[ djoka_l @ 02.12.2024. 09:56 ] @
Zadatak nema jednoznačno rešenje.
2r + 1 + x = 4 - x
r=3/2 - x
Onako kako si nacrtao, deluje da je x=0 i da je r=3/2. Mož da bidne al ne mora da znači.
 [ MajorFatal @ 02.12.2024. 12:10 ] @
Zadatak ima jednoznačno rešenje, jer manja kružnica dodiruje sve ostalo, u četri tačke, tri linije i luk kružnice.
[ djoka_l @ 02.12.2024. 14:19 ] @
Dokaži.
Moje rešenje pokazuje da ima više rešenja.
[ MajorFatal @ 02.12.2024. 15:29 ] @
Osim što manja upisana kružnica dodiruje 4 tačke, dve normale odsecaju na prečniku delove koji su dugački 4 i 1 ... Prema tome manja kružnica je jednoznačno određena
[ djoka_l @ 02.12.2024. 15:46 ] @
Ma nije, vidis da je moja slika drugacija od tvoje.
Postoji beskonacno mnogo upisanih kruznica koje su upisane u vecu i tangentne su na vecu kruznicu i precnik vece kruznice.
Takodje, i ti deovi kruznice koji se odsecaju mogu biti isti.
Da je zadat precnik vece kruznice, bilo bi jendoznacno.
Dokazi tako sto ces izaracunati oi pokazati postupak.
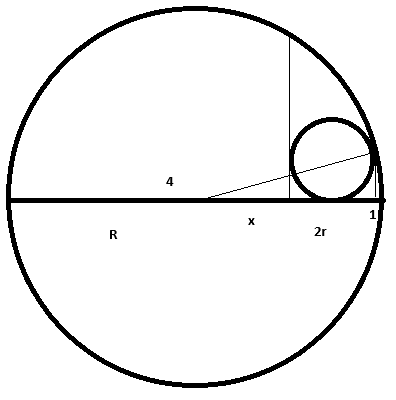
Evo ja sam nacrtao sliku gde je normalna na tangentu koja je zajednicka za obe kruznice na rastojanju x naprecniku vece kruznice mereno od od vertikale manje kruznice na precnik.
Imam komade od 1 i 4 desno i levo od manje kruznice, ali to ne odredjuje jednoznacno manju (a ni vecu) kruznicu.
[ MajorFatal @ 02.12.2024. 17:15 ] @
Citat: djoka_l:
Takodje, i ti deovi kruznice koji se odsecaju mogu biti isti.
Osim što manja kružnica dodiruje sve 4 strane, 3 linije i kružnicu, normale na prečnik veće kružnice ih dele po dužini na 4 i 1, a to je ujedno i odnos 4 : 1 , ispod pravilnog luka.
Prema tome jednoznačno .. [ MajorFatal @ 03.12.2024. 23:04 ] @
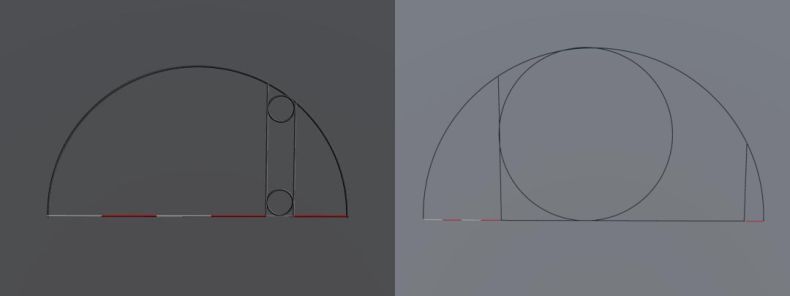
Naravno da postoji koliko god hoćeš polukružnica čije normale na prečnik će odseći dva spoljna odsečka u dužinama 4 i 1, ali nisu sve takve da može da se upiše kružnica koja dodiruje dve normale, prečnik, i luk ... kao na slici, levo upisane kružnice ne dosežu do prečnika ili luka, desno ne mogu da dodiruju luk i prečnik a da istovremeno dodiruju obe normale ...
Kad smo već kod slika djoka_I na tvojoj slici si upisao 4 i 1, ali duži pored kojih stoje te brojke deluju više kao da su odnosu 20 : 1 [ jans @ 04.12.2024. 13:28 ] @
Zadatak nije težak i ima jedinstveno rešenje r=2.
[ MajorFatal @ 04.12.2024. 14:14 ] @
Eh sad baš okruglo 2, je l ima neki postupak tu il se samo kaže?
[ jans @ 04.12.2024. 16:02 ] @
Napisao sam da zadatak nije težak, to znači da postoji postupak. A taj rezultat može da se proveri. Pošto je rastojanje između normala jednako prečniku male kružnice (vidi sliku u prvom postu), prečnik velike kružnice je 2R=4+4+1, pa možemo konstruisati te kružnice ( može i pomoću Geogebre). Drugi način je pomoću analitičke geometrije. Neka je prečnik veće kružnice na osi x a centar manje kružnice na osi y. Jednačine manje, odnosno veće kružnice su
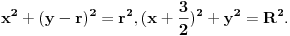
Ako rešimo ovaj sistem jednačina, utvrdićemo da kružnice imaju jednu zajedničku tačku - dodiruju se ( i ovo može da se proveri pomoću Geogebre).
[ miki069 @ 04.12.2024. 16:26 ] @
Odakle se "vidi" da je prečnik velike kružnice 9?
[ jans @ 04.12.2024. 20:31 ] @
Na slici koja je u prvom postu (onom kojim si otvorio ovu temu) prečnik veće kružnice se sastoji iz tri duži: prva je dužine 4, druga duž, duž između normala,jednaka je prečniku male kružnice odnosno 2+2, a treća duž je dužine 1.
[ MajorFatal @ 04.12.2024. 21:39 ] @
Citat: jans:
Napisao sam da zadatak nije težak, to znači da postoji postupak. A taj rezultat može da se proveri. Pošto je rastojanje između normala jednako prečniku male kružnice (vidi sliku u prvom postu), prečnik velike kružnice je 2R=4+4+1, pa možemo konstruisati te kružnice ( može i pomoću Geogebre).
Najviše što možeš da napišeš je: prečnik velike kružnice je 2R=4+2r+1, jer ti nigde u postavci zadatka nije rečeno da je duž između normala dužine 4.
Citat: Drugi način je pomoću analitičke geometrije. Neka je prečnik veće kružnice na osi x a centar manje kružnice na osi y. Jednačine manje, odnosno veće kružnice su
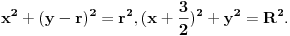
Ako rešimo ovaj sistem jednačina, utvrdićemo da kružnice imaju jednu zajedničku tačku - dodiruju se ( i ovo može da se proveri pomoću Geogebre).
To je super što se dodiruju, sad još samo manja upisana kružnica treba da dodiruje i prečnik velike, i obe normale, i da normale na prečniku odsecaju delove u dužinama 4 i 1, sve drugo si već rešio :)
[ miki069 @ 04.12.2024. 22:55 ] @
Citat: jans:
Na slici koja je u prvom postu (onom kojim si otvorio ovu temu) prečnik veće kružnice se sastoji iz tri duži: prva je dužine 4, druga duž, duž između normala,jednaka je prečniku male kružnice odnosno 2+2, a treća duž je dužine 1.
Nismo mi otvorili temu.
Gospodin Major je otvorio temu.
Oslovljavaj ga sa vi gospodine Majore, a ne sa ti.
Nekulturno je.
Ako imaš rešenje, izloži ga.
Predhodni postovi su bili nejasni. [ jans @ 04.12.2024. 23:21 ] @
Pošto u režimu izmene poruka ne vidim mogućnost citiranja, napominjem da je ova poruka odgovor članu MajorFatal.
Nisi pažljivo pročitao moje poruke. Napisao sam da je rešenje zadatka r=2 ali nisam napisao kako se rešava zadatak. A pošto si posumnjao u rešenje, napisao sam kako može da se proveri da je to stvarno rešenje. Konstruiše se kružnica sa prečnikom 9 i jedan njen prečnik. Onda konstrišemo dve normale na prečnik, jednu na udaljenosti 4 od levog, a drugu na udaljenosti 1 od desnog kraja prečnika. Drugu kružnicu konstruišemo tako da dodiruje normale i prečnik prve kružnice (njen centar je na simetrali duži koja je između normala, a poluprečnik dužine 2). Ona će dodirivati i prvu kružnicu. To može da se odradi sa lenjirom i šestarom, ali je jednostavnije pomoću Geogebre (ili nekog sličnog alata). Napominjem još jednom, to je samo jedna od mogućnosti kako da se proveri da je poluprečnik manje kružnice ( rešenje koje se traži ) dužine 2.
A ako želiš da rešiš zadatak, možeš to uraditi pomoću sličnosti, odnosno korišćenjem potencije tačke u odnosu na kružnicu.
P.S.
Čini mi se da sam ti i ranije savetovao da instaliraš program Geogebra. Besplatan je, jednostavan za korišćenje, možeš ga koristiti na srpskom jeziku. Pomoću njega se jednosavno vrše konstrukcije ( i u prostoru), a može da rešava jednačine, izračuna integrale, ...
[Ovu poruku je menjao jans dana 05.12.2024. u 00:36 GMT+1]
[ MajorFatal @ 05.12.2024. 00:11 ] @
Ah mnogo jasnije, jeste rešenje 2, pošto su neki uspeli da reše kako su znali i umeli, posle toga je postavljač zadatka demonstrirao i to što ti spominješ, to jest rešenje istog zadatka, ali bez korišćenja nekih trigonometrijskih funkcija čini mi se .. to sam čuvao da postavim kao nastavak tj. drugi deo ovog zadatka .. ali prvo da neko reši bilo kako ..
[ miki069 @ 05.12.2024. 18:09 ] @
Ne uspevam da ga rešim.
Da povučem zajedničku tangenta na obe kružnice?
[ jans @ 05.12.2024. 22:12 ] @
Podnožja normala na prečnik polukružnice obeležimo sa B i C, središte polukružnice je tačka S, centar upisane kružnice O, a T je tačka dodira upisane kružnice i prečnika. Sa R obeležimo poluprečnik polukružnice, a sa r poluprečnik manje kružnice. Prema uslovima zadatka je AB=4, CD=1. Pošto upisana kružnica dodiruje normale i prečnik sledi da je FB=BT=TC=CG=r. Sada imamo da je 2R=AD=AB+BT+TC+CD=4+r+r+1, odnosno prvu jednačinu 2R=5+2r.
Odredimo duž ST: ST=SD-DC-CT=R-1-r.
Zajedničku tačku-tačku dodira kružnica obeležimo sa E. Ta tačka pripada pravoj određenoj centrima kružnica, odnosno taćke S,O,E jesu kolinearne pa pomoću potencije tačke S u odnosu na kružnicu k(O,r) dobijamo da je ST 2=SP•SE , odnosno drugu jednačinu (R-1-r)2=(R-2r)R. A dobijeni sistem kvadratne i linearne jednačine nije komplikovan.
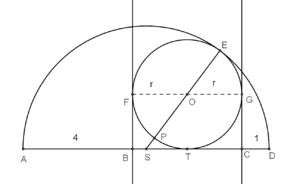 [Ovu poruku je menjao jans dana 05.12.2024. u 23:23 GMT+1]
[Ovu poruku je menjao jans dana 05.12.2024. u 23:23 GMT+1][ MajorFatal @ 05.12.2024. 23:07 ] @
Rešenje, i zaključak da je sistem jednačina jednostavan su verovatno tačni, ali ja ni reč nisam razumeo .. moje pitanje je kako si znao da je tačka S desno od tačke B? Kako možeš da znaš i zaključiš da B nije desno od S na x koordinatnoj osi? Kad bi B bilo desno u odnosu na S - imalo veću vrednost na x osi, cela računica bi bila malo drugačija ... ? Ili ista? ???
[ MajorFatal @ 05.12.2024. 23:47 ] @
Citat: miki069:
Ne uspevam da ga rešim.
Da povučem zajedničku tangenta na obe kružnice?
Ta eto, slično pitanje kao za jans-a, tangenta se lako povlači, kad bi znao gde su centar velike i manje kružnice, ali na koji način da znaš .. ?
A ja mogu kao u stara dobra vremena foruma da zapretim, ako niko ne reši za tri dana postaviću svoje rešenje :)
[ jans @ 06.12.2024. 00:30 ] @
Citat: MajorFatal:
.. moje pitanje je kako si znao da je tačka S desno od tačke B? Kako možeš da znaš i zaključiš da B nije desno od S na x koordinatnoj osi? Kad bi B bilo desno u odnosu na S - imalo veću vrednost na x osi, cela računica bi bila malo drugačija ... ? Ili ista? ???
Ako ti nije jasno skiciraj pa zaključuj na osnovu skice. Može tačka da bude i sa druge strane ali se dobija simetrična slika, levi odsečak će biti 1 a desni 4.
[ miki069 @ 06.12.2024. 09:01 ] @
Bravo Jans. Hvala.
Ja sam crtao tangentu i dobijao mnogoooo nepoznatih.
Majore, kad spojiš centar male kružnice i tačku u kojoj se dodiruju kružnice dobijaš pravu p koja je normalna na zajedničku tangentu.
Na toj pravoj p se nalazi i centar velike kružnice S.
Nikav problem ne predstavlja što je Jans pretpostavio da je R velike kružnice veći od 4.
Da je pretpostavio da je manji od 4, dobio bi kvadratnu jednačinu koja nema realna rešenja.
[ djoka_l @ 06.12.2024. 09:41 ] @
Citat: pomoću potencije tačke S u odnosu na kružnicu k(O,r) dobijamo da je ST2=SP•SE
Ne znam sta ovo znaci [ Ulfsaar @ 06.12.2024. 11:29 ] @
MajorFatal nas je neke zeznuo tako što je napravio precizan crtež, ne skicu, ali je kotirao netačno. Trebalo je umesto 4 da stoji cirka 5,8 da bi se slagalo sa slikom.
[ miki069 @ 06.12.2024. 13:21 ] @
Citat: djoka_l:
Citat: pomoću potencije tačke S u odnosu na kružnicu k(O,r) dobijamo da je ST2=SP•SE
Ne znam sta ovo znaci
Potencija tačke u odnosu na krug.
ST*ST = SP*SE = (kostanta za datu tačku i datu kružnicu) = ST1*ST2.
Gde su T1 i T2 tačke u kojima bilo koja prava iz tače S seče kružnicu.
Lako se dokazuje, ali je dokaz nepotreban, već se koristi u zadacima. [ MajorFatal @ 06.12.2024. 19:54 ] @
Citat: Ulfsaar:
MajorFatal nas je neke zeznuo tako što je napravio precizan crtež, ne skicu, ali je kotirao netačno. Trebalo je umesto 4 da stoji cirka 5,8 da bi se slagalo sa slikom.
:) Još ćeš mi reći da na mom crtežu nisu kružnice nego elipse? I na koji način tačno je to tebe omelo da rešiš zadatak? Zaboravio sam da kažem "slika je samo ilustracija i nije u srazmeri" .. Namerno sam jer su neki na društvenim mrežama učitali ceo crtež koji je išao uz zadatak u geogebru i merili lenjirom i vrlo brzo došli do zaključka da je rešenje tačno 2, ali je i posle toga morao da se dostavi postupak ..
Pošto je jans rešio preko potencije tačke, ostaje kao drugi deo zadatka bez potencije tačke, i sličnosti trouglova ...
[ jans @ 06.12.2024. 21:27 ] @
II. rešenje
Prva jednačina se dobija na isti način kao prva jednačina u prvom rešenju.
Na slici koja je u prvom rešenju treba nacrtati duž OT. Trougao sa temenima S,T,O je pravougli pa primenimo Pitagorinu teoremu
ST2 =SO2-OT2=(SE-OE)2-OT2, odnosno (R-1-r)2=(R-r)2-r2=R2-2Rr ....
[Ovu poruku je menjao jans dana 06.12.2024. u 22:42 GMT+1]
[ MajorFatal @ 07.12.2024. 12:39 ] @
Bravo jans, svaka čast.
Ovaj jans rešava zadatke kao mašina, programirali ga da rešava zadatke. Mr jans, kako vam nije žao da rešite zadatak već na drugi način i tako lišite nekog drugog zadovoljstva da rešava zadatak? Koliko ste vi radosni na skali od jedan do deset kad rešite neki lak zadatak?
Citat: jans:
Pošto u režimu izmene poruka ne vidim mogućnost citiranja, napominjem da je ova poruka odgovor članu MajorFatal.
U režimu izmene poruka, kad se ulogujete na forum, ispod svake poruke se pojavi dva dugmeta sa natpisima: "odgovor sa citatom" i "odgovor na temu", ukoliko želite da citirate samo jednu poruku kliknite na dugme na kome piše Odgovor sa citatom, ceo sadržaj te poruke sa imenom autora će biti prekopiran u prostor za pisanje odgovora. Tu možete i da editujete originalnu poruku, na primer da je skratite ako je predugačka, ili boldujete nešto, ali naravno bez zloupotreba, ne smete dopisivati ništa što originalni autor nije već napisao. Ukoliko želite da citirate više poruka iz teme, kliknite na dugme Odgovor na temu, ispod prostora za pisanje vašeg odgovora pojaviće se spisak prethodnih nekoliko poruka sa teme, možda ćete morati da skrolujete sadržaj ekrana na dole da bi ste to videli, a iznad svake poruke pisaće "citiraj ovu poruku" boldovanim malim slovima, kad kliknete na tekst "citiraj ovu poruku" sadržaj te poruke sa imenom autora će se kopirati u prostor za pisanje odgovora.
Citat: P.S.
Čini mi se da sam ti i ranije savetovao da instaliraš program Geogebra. Besplatan je, jednostavan za korišćenje, možeš ga koristiti na srpskom jeziku. Pomoću njega se jednosavno vrše konstrukcije ( i u prostoru), a može da rešava jednačine, izračuna integrale, ...
[Ovu poruku je menjao jans dana 05.12.2024. u 00:36 GMT+1]
Ma imam geogebru odavno, nego je retko kad uključim. Vidim da ste već koristili dugme za izmenu poruka, dugmad za citiranje poruka su vizuelno identična, i kad ste ulogovani na forum nalaze se ispod svake poruke.
[ Ulfsaar @ 07.12.2024. 19:18 ] @
Citat: MajorFatal:
I na koji način tačno je to tebe omelo da rešiš zadatak?
Kako na koji, pa je l' ti misliš da ja znam šta radim? Držalo me je u zabludi.
Počeli su bili da se javljaju ljudi koji znaju matematiku, a ja sam se pitao šta sad ovi filozofiraju kad je odgovor trivijalan tj R=4, a r=1,5. :)
Međutim, kada sam kasnije to i nacrtao, video sam da mala kružnica ne može da dodirne veću. [ MajorFatal @ 07.12.2024. 21:21 ] @
Pa to je što bi rekli, samo tvoj problem .. niko ti nije rekao ništa .. :)
[ jans @ 08.12.2024. 11:54 ] @
Citat: MajorFatal:
U režimu izmene poruka, kad se ulogujete na forum, ispod svake poruke se pojavi dva dugmeta sa natpisima: "odgovor sa citatom" i "odgovor na temu"... Znam kako se ubacuje citat, međutim, pošto sam poslao poruku a kasnije odlučio da je menjam, posle klika na dugme "Izmena", na ekranu se pojavila poruka koju želim da menjam, a ostale poruke u ovoj temi, ni posle skrolovanja ekrana nisu bile vidljive. Evo i sada dok pišem ovu poruku, posle ubacivanja citata, druge poruke ni posle skrolovanja ne vidim. U svakom slučaju, hvala na odgovoru.
A na sledeće pitanje
Citat: MajorFatal:
Mr jans, kako vam nije žao da rešite zadatak već na drugi način i tako lišite nekog drugog zadovoljstva da rešava zadatak?
odgovor je sledeći: Ako mi je neki zadatak zanimljiv i želim da ga rešim, a u međuvremenu neko "okači" poruku sa rešenjem, tu poruku ignorišem. Pročitam je tek pošto sam rešio zadatak ili ako sam, posle nekoliko neuspelih pokušaja, odustao od rešavanja.
A razlog da pošaljem drugo rešenje je rečenica Citat: MajorFatal:A ja mogu kao u stara dobra vremena foruma da zapretim, ako niko ne reši za tri dana postaviću svoje rešenje :)
u jednoj od prethodnih poruka. Tu rečenicu sam shvatio kao provokaciju onim članovima foruma koji prate ovu temu.
[Ovu poruku je menjao jans dana 08.12.2024. u 13:52 GMT+1][ MajorFatal @ 08.12.2024. 21:16 ] @
Kao što rekoh, kad se ulogujete ispod svake poruke se pojave dva dugmeta, Odgovor sa citatom, i Odgovor na temu, ako kliknete na dugme Odgovor na temu, desetak poslednjih poruka će biti izlistano ispod prostora za pisanje odgovora, i iznad svake će biti link-tekst "citiraj ovu poruku" ...
Na koji način unapred znaš da je poruka baš sa tačnim rešenjem, ako je ne pročitaš do kraja, da bi znao da je ne čitaš, i ne kvariš sebi zadovoljstvo rešavanja? Šta ako je poruka sa na pogrešan način rešenim zadatkom, onda bi trebalo pročitati to da bi se ispravila greška?
Jeste bila provakacija, ali i šala, pre dok je bilo više ljudi na forumu bilo je i situacija, evo zadatak, ako niko ne reši za tri dana postaviću i tačno rešenje.
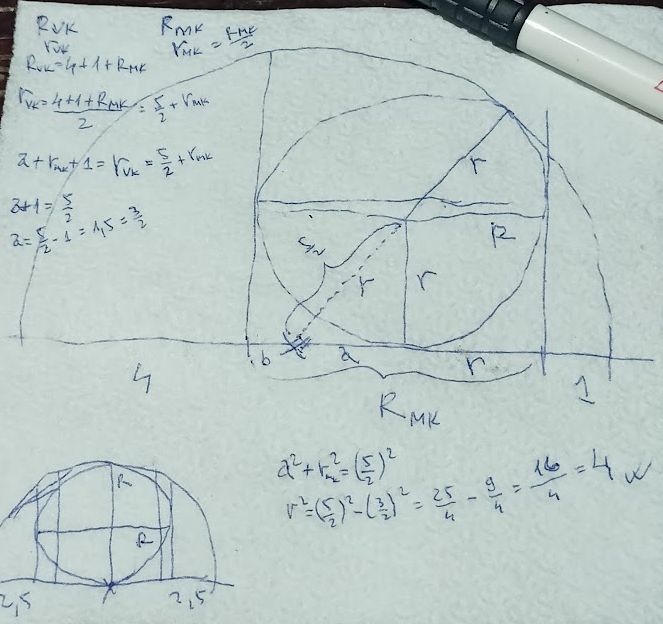
A temu sam otvorio i zadatak postavio ionako samo da se pohvalim, ovo je mola letošnja polusatna bravura, i to u kupaćim gaćama pored jezera, konobar mi pozajmio salvetu i hemijsku :) Ne kažem da nije bilo teško, malo falilo da osustanem, ali: poluprečnik veće polu kružnice da se izraziti na dva različita načina, a odatle može da se dobije ono što sam ja obeležio sa a (kod kolege jansa duž ST), a odatle posle može malo r ...
Ono prethodno je bilo hladno računarsko rešenje, a ovo moje je toplo, ljudsko :)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|