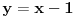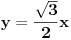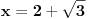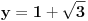[ jans @ 23.12.2024. 21:15 ] @
|
[ Nedeljko @ 24.12.2024. 13:31 ] @
Evo šta je šablonsko rešenje:
Nacrta se sve korišćenjem lenjira, šestara i uglomera i izmere uglovi. Tako znamo koji su iskazi tačni i ostajemo samo da ih dokažemo. Traženi ugao je 75 stepeni. Dvostruka vrednost je 150 stepeni. Tangens traženog ugla je pozitivan, a tangens dvostrukog ugla je 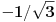 . Ako to dokažemo, onda iz pozitivnosti traženog ugla zaključujemo da je ugao oštar, a iz tangensa dvostrukog ugla da je ugao oblika . Ako to dokažemo, onda iz pozitivnosti traženog ugla zaključujemo da je ugao oštar, a iz tangensa dvostrukog ugla da je ugao oblika 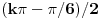 zaneko celobrojno zaneko celobrojno  , pri čemu je jedino rešenje , pri čemu je jedino rešenje 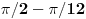 . .Dakle, treba izračunati tangens traženog ugla i tangens dvostrukog ugla. Najpre se sve postavi u koordinatni sistem (može se odabrati da je duž BD jedinična) i odrede koordinate presečne tačke pravih AB i AD. Onda se lako odredi i tangens traženog ugla, koji se najpre racionališe, a onda izračuna tangens dvostrukog ugla po formuli za tangens dvostrukog ugla. [ MajorFatal @ 25.12.2024. 17:10 ] @
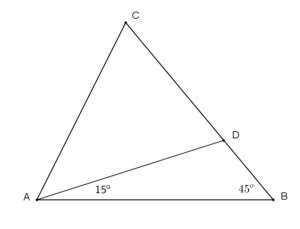
U trouglu ABD treći ugao je 120 stepeni, njemu spoljni ugao ADC je 60 stepeni. Po uslovu zadatka CD = 2DB, ako DB obeležimo kao X, CD = 2X, ali umesto 2X, na sredini duži CD odredim tačku i nazovem je E, pa umesto CD = 2X pišem CE = X i ED = X ...
Iz ugla kod B da se konstruisati duž ili poluprava pod uglom od 15 stepeni u odnosu na AB, ta poluprava presećiće AD u novoj tački F. Ujedno poluprava je ugao od 45 stepeni kod temena B podelila na uglove od 15 i 30 stepeni. Trougao ABF je jednakokraki, sa dva ugla od po 15 stepeni, preostali ugao kod F je 150 stepeni, njemu spoljašnji ugao BFD je 30 stepeni. Trougao BFD je jednakokraki, jer ima dva ugla po 30 stepeni, pa je i dužina FD takođe jednaka X kao i BD ... Ako spojim tačke E i F, dobiće se jednakokraki trougao koji ima dve stranice dužine X, to su stranice ED i FD, međutim ugao između njih je 60 stepeni, sledi da preostala dva ugla u zbiru daju 120 stepeni, a pošto su međusobno jednaki da su oba po 60 stepeni, to jest da je trougao FED jednakostranični ... 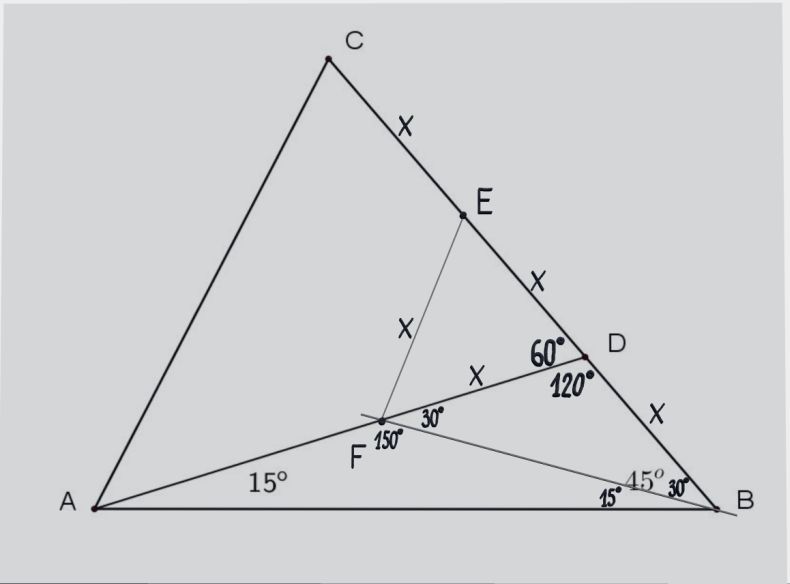 S obzirom da su tačke C, D i F podjednako, za udaljenost X, udaljene od tačke E moguće je konstruisati kružnicu sa centrom u E, koja prolazi kroz sve tri tačke C, D i F. Duž CD je prečnik te kružnice, a ako spojimo tačke C i F, trougao DFC je konstruisan iznad prečnika kružnice i trećim temenom F leži na kružnici. Svaki takav trougao konstruisan iznad prečnika sa trećim temenom na kružnici je pravougli, sa pravim uglom kod temena koje leži na kružnici (mimo prečnika) u ovom slučaju kod temena F, ugao DFC je prav, i iznosi 90 stepeni. Njemu spoljni ugao AFC je takođe prav i iznosi 90 stepeni. S obzirom da su u trouglu DFC uglovi 60 i 90 stepeni, sledi da je treći ugao, kod trećeg temana C jednak 30 stepeni, tj ugao FCD = 30 stepeni. Trougao ABF je jednakokraki, sa dva ugla po 15 stepeni, ako dužinu BF označimo kao a, drugi krak AF će takođe biti dužine a. I trougao BFC je takođe jednakokraki, sa dva ugla od po 30 stepeni, pošto smo dužinu BF obeležili kao a, i dužina CF će isto iznositi a. Trougao AFC je isto jednakokraki, sa dve katete koje su dužine a, između je prav ugao, sledi da su preostala dva ugla jednaka i da iznose po 45 stepeni, tj uglovi FAC i FCA = 45 stepeni. Traženi ugao ACB jednak je zbiru uglova ACF i FCD to jest jednak 45 + 30 = 75 stepeni. Preostali ugao u trouglu BAC jednak je 45 + 15 = 60 stepeni. 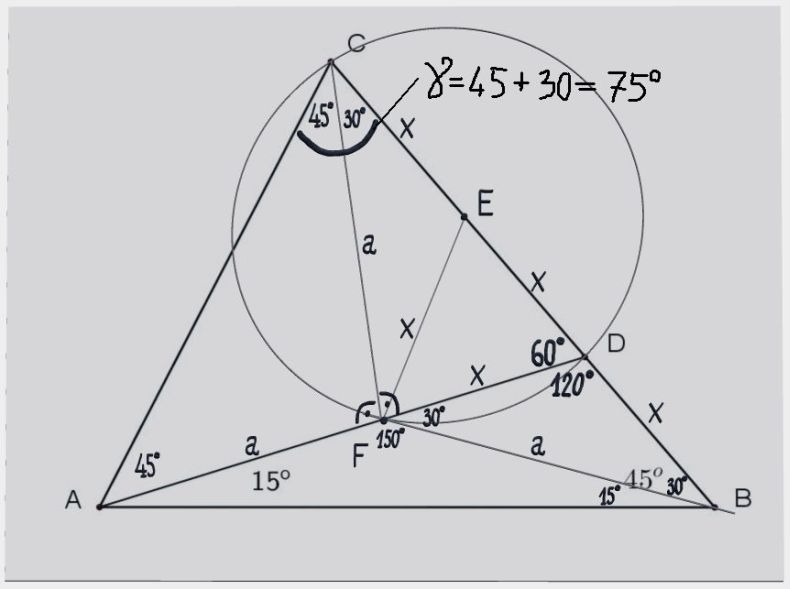 [ feveh @ 25.12.2024. 17:20 ] @
Imamo
ugao BDA 120 stepeni ugao ADC 60 stepeni ugao (alfa1) DAB 15 steni ugao (beta) ABC 45 sstepeni i nepoznat ugao (alfa2) DAC. Ako je alfa unutrašnji ugao tačke A trougla ABC i gama unutrašnji ugao temena C tog trougla tada je: alfa = alfa1 + alfa2 alaf1 = 15 alfa2 + gama = 120 alfa = 135 - gama, 0 < gama < 135. Tek toliko da osetimo problem. A sad račun uz uobičajene oznake: a = 3 DC = 2 sin(120)/c = sin(15)/1 c=sin(120)/sin(15) sin(45)/AD = sin(15)/1 AD = sin(45)/sin(15) b^2 = AD*AD + DC*DC - 2 * AD * DC * cosin(60); Izračunao sam b^2 i c, a je zadato. Imam trougao ABC, pa je cos(alfa) = (b^2 + c^2 - a^2) / (2*b*c) = 0.5 odakle alfa=60, gama=75. Ja sam bio dovoljno lud da sve to računam a ko je pametan nek proveri. [ jans @ 25.12.2024. 20:25 ] @
U prethodna tri posta imamo tri različita rešenja zadatka. Nedeljko je rešio zadatak, i on sam kaže, „šablonski“. Postupak koji navodi feveh, iako jednostavniji od prethodnog, takođe je šablonski.
Razlog za postavljanje ovog zadatka na forum je treći način rešavanja, bez analitičke geometrije i trigonometrije. Taj način je kraći od prethodnih, iziskuje samo osnovno poznavanje geometrije, a svodi se na primenu podudarnosti truouglova ( to smo učili u VI osnovne ). „Najbliže“ tom rešenju je rešenje koje navodi MajorFatal, samo što ga je on malo zakomplikovao. Rešenje može biti jednostavnije i kraće. [ Nedeljko @ 25.12.2024. 22:32 ] @
Razlog mog načina pisanja (zanemarujući očigledne jezičke greške) je opštost. Kako izaći iz okvira ovog jednog zadatka i rešavati mnoge slične zadatke? Štosovima koji su primenljivi samo na jedan zadatak se pribegava kada nema drugog rešenja, a radi se o nekoj važnoj činjenici.
[ MajorFatal @ 26.12.2024. 13:09 ] @
Pa i ja sam rešavao tako da bude univerzalno rešenje, da ne trebaju tangensi, sinusi .. :)
Ču ja zakomplikovao, ja još i skratio, ispustio sam da napišem da tek kad se pokaže da je FED jednakostraničan, tek tad može da se napiše da je FE = X .. A vi gospodine jans, zašto ste koristili dva različita fonta za ispisivanje vrednosti uglova, hteli ste da nas zbunite da ne rešimo zadatak?  [ feveh @ 26.12.2024. 15:15 ] @
Baš me zanima "cena" dokaza da je FE == X :)
@jans je dobar matematičar i pretpostavio sam da ima na umu primenu stavova podudarnosti. Ali sam od konstruktivnog dokaza za VI razred osnovne odustao kad sam video da na prave odredjene sa AB, AC i AD ne mogu da primenim teoremu o nesusednim uglovima. Odnosno konstruktivni dokaz se toliko komplikuje da gubi smisao a ta konstrukcija ima ograničenu primenu. Zato sam se okrenuo trigonometriji a prednost takvog prilaza je što dobijam numeričku vrednost. Rešenje metodama anlitičke geometrije ima svoju neposrednu primenu u na primer računarskim animacijama ili u artiljeriji. Ako tačku A postavimo u centar koordinatnog sistema onda je lako odrediti nagib prave BC a time i koordinate tačke C. [ Nedeljko @ 27.12.2024. 04:13 ] @
Prema ideji i oznakama člana MajorFatal:
Neka je E središte duži CD. Tada je CE=ED=DB. Ovu dužinu označimo sa x. Ugao ADB je 120 stepeni (jer je zbir uglova u trouglu ADB jednak 180 stepeni), pa je ugao CDA 60 stepeni. Neka je F tačka na duži AD tako da ugao DBF bude 30 stepeni i samim tim podudaran uglu DFB. Važi DF=DB=x. Pošto je ugao CDA 60 stepeni, važi EF=x. Tačke C, D i F leže na krugu sa centrom E, pa je ugao CFD je prav kao periferijski nad prečnikom CD, pa je ugao EFC jednak 30 stepeni. Iz FE=EC zaključujemo da je ugao ECF podudaran uglu EFC koji je 30 stepeni, pa je BF=BC. Iz AF=BF=BC sledi da su uglovi FAC i FCA podudarni, pa pošto je ugao AFC prav, ugao ACF je 45 stepeni, pa je ugao CAD jednak 75 stepeni. Ne znam da li sada neko ima nedoumica oko njegovog rešenja. [ MajorFatal @ 27.12.2024. 19:56 ] @
Eh, hvala Nedeljko, ja stvarno "preko brda i dolina" kako je govorila nastavnica matematike svojevremeno, kad ispišemo rešenje koje je duže nego što bi trebalo.
Možda je mogla samo da se spusti normala iz tačke C na AD, isto bi se dobila tačka F, takođe simetrala duži BC dala bi F i na dalje sve isto. Primetio sam i da se trouglovi EFB i DFC slični, pa se negde tu možda krije neko kraće rešenje za koje pita jans ... [ feveh @ 27.12.2024. 23:08 ] @
To "cena" nije osporavanje tačnosti ni metoda ni dokaza nego se odnosi na vreme, ljudske i računarske resurse utrošene na pronalaženje rešenja.
Meni izgleda da je za pronalaženje tog rešenja korišćena neka aplikacija za inženjerske konstrukcije. To nije isto kao rad "peške". [ miki069 @ 28.12.2024. 11:26 ] @
Pošovani kolega Jans je trebao da definiše za koji nivo je zadatak.
Ako je za 6,7,8 razred osnovne škole, onda jedino korektno rešenje je ono koje je dao Major. [ MajorFatal @ 28.12.2024. 12:16 ] @
Citat: feveh: To "cena" nije osporavanje tačnosti ni metoda ni dokaza nego se odnosi na vreme, ljudske i računarske resurse utrošene na pronalaženje rešenja. Meni izgleda da je za pronalaženje tog rešenja korišćena neka aplikacija za inženjerske konstrukcije. To nije isto kao rad "peške". Naravno da je korišćena inžinjerska aplikacija Kliker.com ChatGpt 6.01, ali su još zanimljiviji hardveri na kojima je tarana, tkz papir i olovka .. sa mnogo predomišljanja i odustajanja. 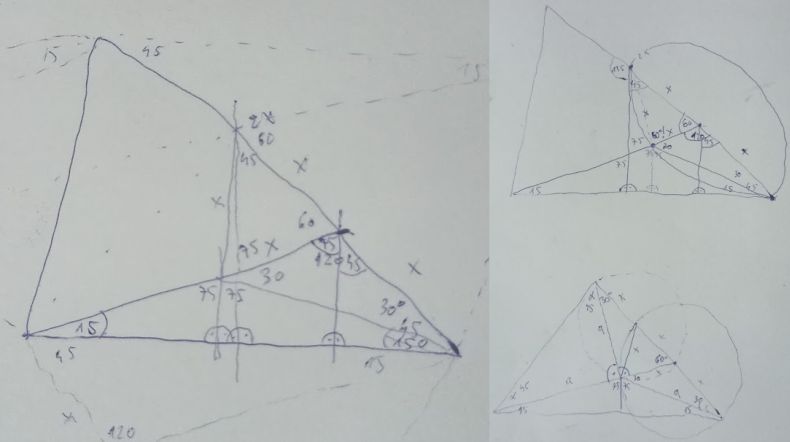 Nego sad kad si me naterao da ponovo pogledam slike, jedva sam se otarasio ove druge kružnice koju sam crtao u centru sa D, te video da mi ne treba dva ugla od po 75, međutim u međuvremenu se ispostavilo da je 75 rešenje, tako da ako se spusti normala iz C na AB odmah se dobija trougao koji je sličan trouglu ABC, jedino što ne znam kako bih dokazao da su slični :) Možda na to mnogo kraće rešenje aludira jans .. 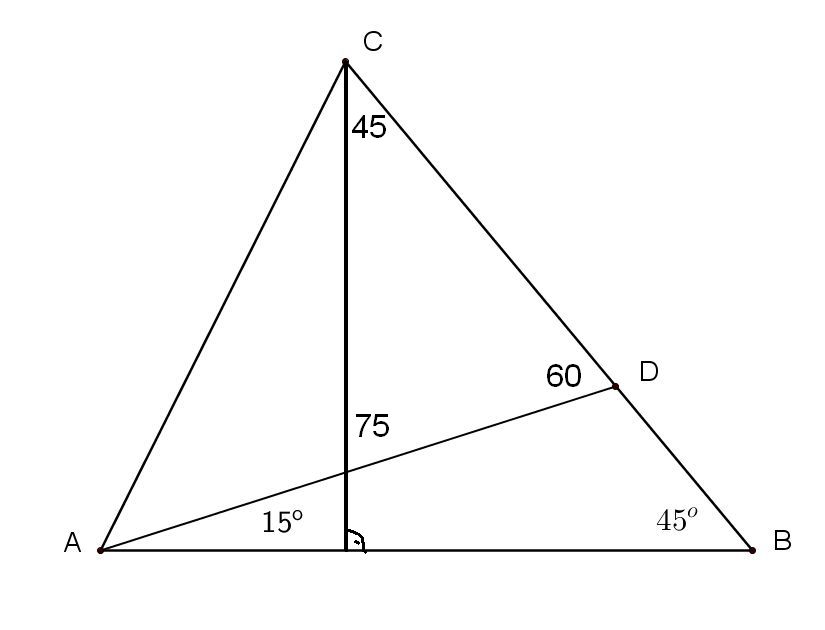 [ miki069 @ 29.12.2024. 17:20 ] @
Nisam stigao ni da pokušam da rešim zadatak.
Molio bih pošovanog kolegu Jansa, da u 20024-toj godini ne objavljuje to kraće rešenje. Da probaju i ostali. [ Nedeljko @ 31.12.2024. 16:20 ] @
Malo drigačije rešenje.
Prvo se odrede laki uglovi. Tačka E se izabere kao simetrala duži CD. Duži CE, ED i DB. Obzirom da je ugao ADC jednak 60 stepeni, tačka F se izabere tako da trougao DEF bude jednakostranični. Trougao BDF je jednakokraki pa uglovi FBD o BFD imaju po 30 stepeni. Trougao BCF je simetričan u odnosu na simetralu stranice BC, pa je jednakokraki, pa ugao ECF ima 30 stepeni. Trougao CFE je jednakokraki, pa ugao CFE ima 30 nstepeni, pa je ugao CFA prav. SVaka od duži AF i CF je podudarna duži BF, pa je trougao AFC jednakokraki, pa uglovi CAF i AFC imaju po 45 stepeni. [ miki069 @ 31.12.2024. 18:57 ] @
Trebalo je samo da se spusti visina iz temena C na duž AD.
To je tačka F. Da bi se iskoristila osobina da se u pravouglom trouglu naspram ugla od 30 stepeni nalazi kateta duplo manja od hipotenuze. Račun je objasnio Nedeljko. [Ovu poruku je menjao miki069 dana 31.12.2024. u 20:08 GMT+1] [ miki069 @ 31.12.2024. 19:54 ] @
Bez ove Nedeljkove ideje, račun preko: jednom kosinusna i 3 puta sinusna teorema nije toliko mnogo smoran.
Problem je bio da se prepozna potpun kvadrat (žuta boja). [ miki069 @ 01.01.2025. 08:41 ] @
Zadatak liči na:
https://www.elitesecurity.org/t480726-0#3515544 Ne po tekstu, nego po tome koliko je teže rešiti ga upotrebom trigonometrije. [ jans @ 01.01.2025. 12:13 ] @
Postupak rešavanja je najkraći, to je u jednom od prethodnih postova konstatovao i miki069, ako koristimo samo tačku F. Tačka E je suvišna. A tačku F na duži AD možemo odrediti na tri načina:
- tako da ugao ABF bude 15o; - tako da bude DF=DB; - kao podnožje normale iz temena C na duž AD. Bez obzira kako tačku F odredimo, postupci rešavanja se razlikuju samo u redosledu primene osobina trougla ( osobine uglova trougla, jednakokrakih trouglova i, posredno, podudarnost trouglova ). [ Nedeljko @ 01.01.2025. 20:30 ] @
Pokretač teme je u početnoj poruci tvrdio da je zadatak počan. Po čemu je poučan?
[ MajorFatal @ 02.01.2025. 14:00 ] @
Citat: jans: Postupak rešavanja je najkraći, to je u jednom od prethodnih postova konstatovao i miki069, ako koristimo samo tačku F. Tačka E je suvišna. A tačku F na duži AD možemo odrediti na tri načina: - tako da ugao ABF bude 15o; - tako da bude DF=DB; - kao podnožje normale iz temena C na duž AD. Bez obzira kako tačku F odredimo, postupci rešavanja se razlikuju samo u redosledu primene osobina trougla ( osobine uglova trougla, jednakokrakih trouglova i, posredno, podudarnost trouglova ). Pa ne znam baš, kad se odredi F tako što je ugao ABF 15o, prvo se pokazuje da je DF = X, pa EF = X, pa da je moguće konstruisati kružnicu, pa da je ugao CFD periferni, pravougli, pa ostalo. Ne znam kako bi ovo išlo unazad počevši od podnožja normale iz temena C na duž AD, ili iz DF = DB, a sve bez tačke E? Niti da bi postupak bio značajno kraći? [ 5thdimension @ 02.01.2025. 14:57 ] @
Nedeljko je uveo tačku E da bi mogao pokazati AF = BF.
Za sada je to rešenje najkraće jer niko nije pokazao da je naspram ugla od 30 stepeni stranica dužine polovine dužine hipotenuze. [ Nedeljko @ 02.01.2025. 21:42 ] @
Ništa Nedeljko nije uvodio, nego je iskoristio MajorFatal-ovo rešenje.
Može bez tačke E, kao što je jans tvrdio. 1. Izabere se tačka F tako da ugao ABF ima 15 stepeni. To je moguće jer je 15 stepeni manje od 45 stepeni koliko ima ugao ABC. 2. Pošto je trougao ABF jednakokraki, važi AF=BF. 3. Ugao ADB ima 180-15-45=120 stepeni. 4. Ugao FBD ima 45-15=30 stepeni. 5. Ugao BFD ima 180-30-120=30 stepeni. 6. Trougao BFD je jednakokraki, pa je BF=FD. 7. Ugao CDF ima 180-120=60 stepeni. 8. Pošto je FD=BD=2CD i ugao CDF ima 60 stepeni, ugao CFD je prav. 9. Ugao FCD ima 90-60=30 stepeni. 10. Trougao BCF je jednakokraki, pa je BF=CF. 11. Iz AF=BF=CF sledi da je trougao ACF jednakokraki. 12. Trougao ACF je jednakokraki i pravougli, pa uglovi ACF i CAF imaju po 45 stepeni. 13. Ugao ACB ima 45+30=75 stepeni. Ipak mi nije jasna poučnost zadatka. Edit: Ispravio sam grešku u tački 1 koju je uočio jans. [Ovu poruku je menjao Nedeljko dana 03.01.2025. u 02:23 GMT+1] [ jans @ 02.01.2025. 23:20 ] @
Citat: MajorFatal: Pa ne znam baš, kad se odredi F tako što je ugao ABF 15o, prvo se pokazuje da je DF = X, pa EF = X, pa da je moguće konstruisati kružnicu, pa da je ugao CFD periferni, pravougli, pa ostalo. Ne znam kako bi ovo išlo unazad počevši od podnožja normale iz temena C na duž AD, ili iz DF = DB, a sve bez tačke E? Ako tačku F odredimo tako da je ugao ABF od 15o ( ili da ugao DFB bude od 30o ), imamo trougao BDF sa dva ugla od 30o. Iz toga sledi da su naspram tih uglova jednake stranice, odnosno BD=DF, pa je CD=2BD=2DF. Prema tome u trouglu CDF je jedna stranica dva puta duža od druge a ugao između njih ( ugao kod temena D ) je od 60o. Sledi da je taj trougao polovina jednakostraničnog trougla, dakle pravougli, pa je ugao kod temena C od 30o. Ako nije jasno zašto je taj trougao polovina jednakostraničnog trougla, obrazloženje je sledeće: Ako bi konstruisali jednakostraničan trougao tako da mu je stranica jednaka duži CD i visinom podelili taj trougao na dva podudarna dela, polovina tog jednakostraničnog trougla bi bila podudarna sa trouglom CFD ( na osnovu stava o podudarnosti koji smo obeležavali sa SUS ). U slučaju da tačku F odredimo tako da je DF=DB, sledi da je CD=2DF, ugao kod temena D od 60o, a to je trougao kao u prethodnom slučaju. Međutim, i miki069 je u postu koji je ispred poruke iz koje je navedeni citat, napisao da je dovoljna samo taćka F: Citat: Trebalo je samo da se spusti visina iz temena C na duž AD. To je tačka F. Da bi se iskoristila osobina da se u pravouglom trouglu naspram ugla od 30 stepeni nalazi kateta duplo manja od hipotenuze. Pošto iz temena C spustimo normalu CF na duž AD, imamo pravougli trougao CFD u kojem je jedan oštar ugao kod temena D od 60o. Taj trougao je polovina jednakostraničnog trougla, pa je hipotenuza tog trougla dva puta duža od kraće katete, odnosno CD=2DF, odakle sledi da je DF=DB. A obrazloženje zašto je taj trougao polovina jednakostraničnog trougla, je slično prethodnom ( a svodi se na primenu stava USU ). Prema tome tačka E, a samim tim i ti periferijski i centralni uglovi su nepotrebni. P.S. Pošto je Nedeljko poruku poslao dok sam ja pripremao ovaj post, pa sam tu poruku video tek sada, dopuniću prethodni tekst. Nedeljko u tački 8. navodi zaključak ali bez obrazlaganja i to je sve ok. Ako bi to detaljno objasnio, to bi bilo isto objašnjenje kao jedno od gore navedenih. [Ovu poruku je menjao jans dana 03.01.2025. u 01:10 GMT+1] [ 5thdimension @ 03.01.2025. 00:18 ] @
Citat: Nedeljko 1. Izabere se tačka F tako da ugao ABF ima 30 stepeni. Jel može to malo detaljnije korak po korak? Kako si izabrao F i dobio taj ugao od 30 stepeni? Slično pitanje za Citat: jans Taj trougao je polovina jednakostraničnog trougla, pa je hipotenuza tog trougla dva puta duža od kraće katete, odnosno CD=2DF. A obrazloženje zašto je taj trougao polovina jednakostraničnog trougla, je slično prethodnom ( a svodi se na primenu stava USU ). Nije sporno da se može sve dokazati primenom podudarnosti. Nego je pitanje broja koraka. Dokaz samo tog "obrazloženje" preko podudarnosti za koji ja znam ima bar 6 koraka sve sa onim "primetimo". I onda šta je kraće? [ jans @ 03.01.2025. 00:50 ] @
Citat: 5thdimension: Nije sporno da se može sve dokazati primenom podudarnosti. Nego je pitanje broja koraka. Dokaz samo tog "obrazloženje" preko podudarnosti za koji ja znam ima bar 6 koraka sve sa onim "primetimo". I onda šta je kraće? Napominjem da i Nedeljko u poslednjoj poruci, u tački 8. zaključuje ( bez napomene da je u pitanju polovina jednakostraničnog trougla ) da je trougao pravougli i ima jedan oštar ugao od 60o, bez dokaza, zato što je to poznata činjenica i koristi se bez dokaza. A ako ćemo brojati korake u postupku onako kako ti brojiš, onda oni koji rešavaju zadatak pomoću centralnog i periferijskog ugla, neka dokažu zašto je centralni dvaput veći od periferijskog ugla ( a neko će možda reći da najpre definišu te pojmove ) pa da onda vidimo koji je postupak duži. [ MajorFatal @ 03.01.2025. 08:35 ] @
Vidi stvarno, može bez tačke E .. lepo ..
[ miki069 @ 03.01.2025. 10:24 ] @
Dokaz da se u prvouglom trouglu naspram ugla od 30 stepeni nalazi kateta koja je 1/2*hipotenuza je triijalan.
Samo se docrta još jedan takav trougao i dobije se jednakostraničan trougao. Dokaz da je centralni ugalo =2*periferijski nije težak, ali duže traje. Dokazi sinusne i kosinusne teoreme su lagani i meni jasni. Dokaz adicionih formula za sinus i konus nikada nisam upevao sam da izvedem. Nalazio sam neke dokaze koji mi baš nisu 100% jasni. Zamolo bih link ka nekom dokazu. Bar za sinus(alfa + beta). Ili neki vaš dokaz. Cenim da Nedeljko i Jans to mogu da izvedu. [ 5thdimension @ 03.01.2025. 10:29 ] @
Citat: jans A ako ćemo brojati korake u postupku onako kako ti brojiš Ti si tražio da se svede na ono što se učilo u VI razredu. Stav o 30 stepeni, naspramnoj stranici i hipotenuzi u pravouglom trouglu se ne dokazuje u VI razredu. Osim ako je izmenjen plan i program - nije mi poznato. Ajmo ovako: Nedeljko je izmenio poruku. Sada konstruiše ugao 15 stepeni od ugla 45 stepeni. Kako? jans umesto tačke E i trougla FDE se poziva na jednakostranični trougao koji nije dat u postavci zadatka. [ miki069 @ 03.01.2025. 15:08 ] @
Ne znam koji deo ti nije jasan?
Sva tri načina su ekvivalentna. Idemo ovako: iz tačke C konstuišemo normalu na duž AD. Presek je tačka F. Tada se koristi činjenica da naspram ugla od 30 stepeni se nalazi kateta=1/2*hipotenuza, a važi i obrnuto. Ekvivalencija. Jasno rešenje ili nije? Ako nije, pročitaj pažljvo kako je Nedeljko objasnio ekvivalentan dokaz. Ako i to nije jasno, ili nisi dostojan sagovornik ili si trol. [ Nedeljko @ 03.01.2025. 15:41 ] @
Citat: miki069: Dokaz adicionih formula za sinus i konus nikada nisam upevao sam da izvedem. Ja sam u gimnaziji "otkrio" adicione teoreme sinusa i kosinusa, pre nego što smo ih učili, tako što sam ih samostalno izveo. Trebale su mi za rotaciju u računarskoj grafici. [ miki069 @ 03.01.2025. 16:19 ] @
Taj dokaz sam i tražio.
Može i u posebnoj temi. Zbog važnosti. [ 5thdimension @ 03.01.2025. 16:40 ] @
Citat: miki069 Tada se koristi činjenica da naspram ugla od 30 stepeni se nalazi kateta=1/2*hipotenuza, a važi i obrnuto. To nije činjenica nego se dokazuje. Naravno, ti možeš uraditi sličan zadatak na času i deci na pismenom dozvoliti da ga koriste bez dokaza. Tada deca pišu "... i na osnovu zadatka od petka sledi da su podudarni". Medjutim time se povlači sav onaj materijal iz dokaza "zadatka u petak". Tj. implicitno si konstruisao trougao X'Y'Z' ili nešto slično. Drugo, elementarni zaključak je na primer "ako su date dve prave koje se seku pod uglom alfa onda je ugao beta == alfa jer su unakrsni". To se ne dokazuje jer sledi direktno iz postavke zadatka. To je za VI razred. Medjutim onaj trougao X'Y'Z' nije dat postavkom zadatka. Tako da ja smatram da se tvrdjenje o tom trouglu dokazuje ili se pozovete na "zadatak od petka" a oboje podrazumeva dokonstrukciju trougla X'Y'Z', makar i mentalno. [ MajorFatal @ 03.01.2025. 21:13 ] @
Da, onda i ja mogu da se pobunim, sama izjava da je "jedna stranica dva puta duža od druge" sadrži u sebi tačku E, ne možeš nikako ni izmeriti, ni konstruisati bilo koju duž koja je dva puta duža od neke druge (ili dva puta kraća), sem da dva puta nanosiš prvu duž na drugu, i tako utvrdiš dužinu (ili odrediš polovinu duži tačkom E pa izmeriš da je ona druga jednaka tačno polovini), u svakom tom postupku postoji i koristi se tačka E.
U stvari ona je bila tu već u postavci zadatka sa CD = 2DB, samo se prećutkuje i izostavlja iz opisa postupka ... ? Slično važi i za duž EF, ne možeš koristiti osobine trougla, a da ga ne konstruišeš, sa centrom u E, mslm možeš da bi skratio opis rešenja, i kažeš a ostalo domislite. Ili ima postupak da konstruišem dva puta dužu duž od neke druge bez nanošenja jedne tačke između, ali takav postupak bi, cenim, bio duža procedura od ove već opisane? [ Nedeljko @ 03.01.2025. 21:41 ] @
Citat: Naravno da se tog izvođenja ne sećam, ali je bilo komplikovanije nego što je neophodno. Navešću elegantnije izvođenje. 1. Slučaj dva oštra ugla čiji je zbir oštar ugao. Neka su A, B i C oštri uglovi sa zajedničkim temenom O, gde su p i r kraci ugla C, poluprava q se nalazi unutar ugla C, p i q su kraci ugla A i q i r su kraci ugla B. Izaberimo proizvoqnju tačku P poluprave p različitu od O. Neka je Q podnožje upravne iz P na q i neka je R podnožje upravne iz Q na r. Neka je K podnožje upravne iz P na r, L presek pravih PK i OQ i neka je M podnožje upravne iz Q na pravu PK. Tada važi sledeće: Prave PK i MK su jednake. Prave MK i QR su paralelne kao upravne na OR. Prave MQ i KR su paralelne kao upravne na OK. Prave MQ i MK su upravne. Četvorougao MKRQ je pravougaonik. KR=MQ jer su to naspramne ivice pravougaonika. Ugao MPQ iznosi 90 stepeni minus ugao PLQ, odnosno 90 stepeni minus ugao OLK, odnosno isto koliko i ugao A. 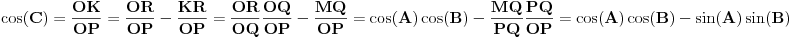 . .2. Slučaj dva oštra ugla čiji je ugao prav. Neka su A i B uglovi koji se dopunjuju do pravog. Tada važi sledeće: Tada je 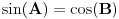 , , 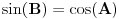 . Kosinus pravog ugla je nula, a isto toliko iznosi i . Kosinus pravog ugla je nula, a isto toliko iznosi i 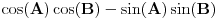 . .3. Slučaj dva oštra ugla čiji je ugao tup: Slučaj je analogan slučaju dva oštra ugla čiji je zbir oštar. Tekst se skoro prepisuje. Neka su A, B i C oštri uglovi sa zajedničkim temenom O, gde su p i r kraci ugla C, poluprava q se nalazi unutar ugla C, p i q su kraci ugla A i q i r su kraci ugla B. Izaberimo proizvoqnju tačku P poluprave p različitu od O. Neka je Q podnožje upravne iz P na q i neka je R podnožje upravne iz Q na r. Neka je K podnožje upravne iz P na r, L presek pravih PK i OQ i neka je M podnožje upravne iz Q na pravu PK. Tada važi sledeće: Prave PK i MK su jednake. Prave MK i QR su paralelne kao upravne na OR. Prave MQ i KR su paralelne kao upravne na OK. Prave MQ i MK su upravne. Četvorougao MKRQ je pravougaonik. KR=MQ jer su to naspramne ivice pravougaonika. Ugao MPQ iznosi 90 stepeni minus ugao PLQ, odnosno 90 stepeni minus ugao OLK, odnosno isto koliko i ugao OLK, odnosno isto koliko i ugao A. 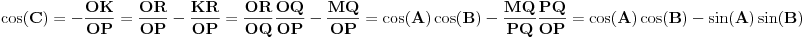 . .Preostali slučajevi se obrađuju svođenjem na slučaj dva oštra ugla i adicionih teorema u slučaju kada je jedan od uglova prav. 4. Slučaj kada je jedan ugao prav, a drugi oštar: Kosinus zbira oštrog ugla A i pravog ugla je minus sinus ugla A, pa jednakost važi na osnovu vrednosti za sinus i kosinus pravog ugla. 5. Slučaj dva prava ugla. Sledi iz sinusa i kosinusa pravih uglova i opruženog ugla. 6. Slučaj kada je neki od uglova veći od pravog. Svodi se na slučaj oštrih uglova predstavljanjem ugla većeg od pravog ugla kao zbira pravog ugla i nekog manjeg ugla i primenom stava o sinusu i kosinusu zbira oštrog i pravog ugla. [ miki069 @ 04.01.2025. 01:40 ] @
5thdimension:
Ako nije jasan dokaz da se u pravouglom trouglu naspram ugla od 30° nalazi kateta=1/2"hipoteza, napisaću ga. Trivijalan je. Rade ga deca u VI razredu osnovne škole. Po tebi ni Pitagorina teorema ne sme da se koristi bez dokaza? [ miki069 @ 04.01.2025. 01:42 ] @
5thdimension:
Ako nije jasan dokaz da se u pravouglom trouglu naspram ugla od 30° nalazi kateta=1/2"hipoteza, napisaću ga. Trivijalan je. Rade ga deca u VI razredu osnovne škole. Po tebi ni Pitagorina teorema ne sme da se koristi bez dokaza? [ 5thdimension @ 04.01.2025. 04:04 ] @
Naravno da ne znam teoremu o polovini dužine u pravouglom trouglu pa zato moram da konstruišem još jedan trougao :)
No sad ozbiljno. Iz ovoga Citat: Pravougli trougao čiji su oštri uglovi 30° i 60° – Matematika za 7. razred https://edukacija.rs/matematik...u-ostri-uglovi-30-i-60-stepeni zaključujem da neki taj stav nauče tek u 7-mom razredu. Da nastavnik može to da uvede u 6-tom razredu napisao sam ovde: https://www.elitesecurity.org/p4092342 Takodje GARANT znam da neki završe 6-ti razred a da ne urade takav zadatak. A nije ni obavezno nego nastavnik samostalno odlučuje (osim ako je izmenjen plan i program za šta ne znam). [ 5thdimension @ 04.01.2025. 04:56 ] @
U medjuvremenu sam pronašao plan i program za VI razred.
Nema nastavna jedinica "osna simetrija". Tako da je pod znakom pitanja da nastavnik može izvesti dokaz navedene teoreme. Odnosno ono što sam napisao da neki ne rade taj dokaz izgleda da je sada pravilo kao posledica redukcije nastavnih planova i programa. [ miki069 @ 05.01.2025. 12:09 ] @
Kolegu Jansa nisam pitao da li je nivo zadatka za VI razred osnovne škole, nego da li je za VI-VII-VIII razred osnovne škole.
Takvo rešenje je izložio Major, a usavršio ga Nedeljko. Iz očajanja sam povukao visinu iz temena C na AD i uradio ga. Posle sam video da je to sadržano u rešenju koje je uradio Nedeljko. Kolega Jans je lepo objasnio da su sva tri rešenja ekvivalentna i ispravna. Ne znam koji deo rešenja ti nije jasan? Ako imaš neko četvrto rešenje, izloži ga. Rešenje za nivo II-III godina srednje škole je detaljno izložila samo moja malenkost. Proveri i javi ako nešta nije jasno. Ako imaš neko drugo rešenje, izloži ga. Bez nekih tvojih rešenja ili (ne)razumevanja izloženih ličiš na neadekvatnog sagovrnika. Ili trola. Ne zbog mene. Osporavati Nedeljku tačno rešenje je baš trolovanje. Uradio je stotine zadataka ovde na forumu i nikada mu nisam našao grešku. Treba imati poštovanje za to. Vidi se i da je kolega Jans profesionalni matematičar. Najmanje završena SM srednja, a možda i MATF. [Ovu poruku je menjao miki069 dana 05.01.2025. u 13:28 GMT+1] [ Nedeljko @ 05.01.2025. 16:58 ] @
Ja ne znam šta se uči u kom razredu škole, ali se uči visina trougla i zna se kako se jednakostranični trougao može podeliti na pola i bez uvođenja pojma osne simetrije.
Dakle, zna se da postoji pravougli trougao čija je jedna kateta upola manja od hipotenuze i kod koga su uglovi 30 i 60 stepeni. Onda se na osnovu SUS stava o podudarnosti trouglova zaključuje da je trougao sa iglom od 60 stepeni i jednom katetom upola manjom od druge pravougli. [ 5thdimension @ 05.01.2025. 18:05 ] @
^miki069
Auh, "nije zbog tebe" nego se sekiraš za Nedeljka. Pročitj temu: Citat: jans Taj način je kraći od prethodnih, iziskuje samo osnovno poznavanje geometrije, a svodi se na primenu podudarnosti truouglova ( to smo učili u VI osnovne ). i po tom uslovu traži se dokaz korišćenjem samo podudarnosti. Upoznaj se sa planovima i programima matematike. U starijim knjigama dokaz da se naspram ugla od 30 stepeni nalazi kateta=1/2*hipotenuza ide preko osne simetrije i nije obavezan deo gradiva. Prema sadašnjem planu osna simetrija nije nastavna jedinica u VI razredu (ostavio sam link pa proveri). Zato "kateta=1/2*hipotenuze" nije put do rešenja odredjen prethodnim uslovom koji je dao jans. Citat: miki069 Rešenje za nivo II-III godina srednje škole je detaljno izložila samo moja malenkost. Rešenje 6 dana pre tebe za II srednje. Još jednostavnije sinus(30 stepeni) = 1/2 pa sam u prvom srednje. MajorFatal je prvi napisao rešenje zasnovano na podudarnosti. Opisani postupak "1. Izabere se tačka F tako da ugao ABF ima 15 stepeni. To je moguće jer je 15 stepeni manje od 45 stepeni koliko ima ugao ABC. " ne znači da se tačka F stvorila niotkuda nego se mora konstruisati. Ugao od 15 stepeni sa temenom u tački B može se konstruisati nezavisno od veličine ugla u temenu B trougla ABC. Normala na srednju tačku duži AB prolazi kroz neku tačku, na primer F, duži AD. Dobiju se dva podudarna trougla (SUS) pa je konstruisan ugao od 15 stepeni u temenu B nezavisno od veličine ugla ABC. Ako postoji neki drugi način "jer je 15 stepeni manje od 45 stepeni" veoma bi me zanimalo kako? [ 5thdimension @ 05.01.2025. 18:08 ] @
^Nedeljko
Nije to sporno nego jans hoće najkraći postupak. [Ovu poruku je menjao 5thdimension dana 05.01.2025. u 19:24 GMT+1] [ Nedeljko @ 05.01.2025. 19:07 ] @
Visina svakog jednakokrakog trougla je simetrala suprotne stranice. Onda možemo primeniti SUS stav o podudarnosti trouglova.
Neka jans sam kaže šta hoće. [ miki069 @ 05.01.2025. 23:22 ] @
Rešenje 6 dana pre mog za II razred srednje škole ne postoji.
Obrati pažnju na izjavu: Ja sam bio dovoljno lud da sve to računam a ko je pametan nek proveri. Ja sam bio pametan i proverio. Kolega Feveh je napisao ideju, ali nema konkretnog računa. Ako uopšte razumeš šta je Feveh napisao. Najverovatnije, ne razumeš. [Ovu poruku je menjao miki069 dana 06.01.2025. u 00:33 GMT+1] [ Nedeljko @ 06.01.2025. 15:36 ] @
[ miki069 @ 06.01.2025. 17:48 ] @
Nedeljko, hvala za izvođenje adicionih formula.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|