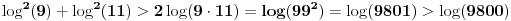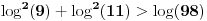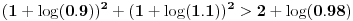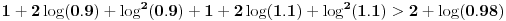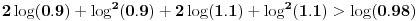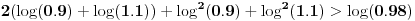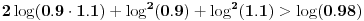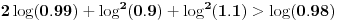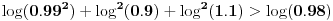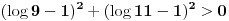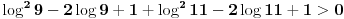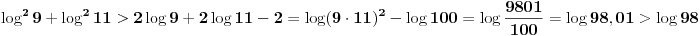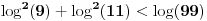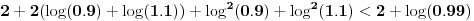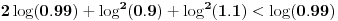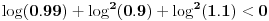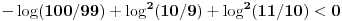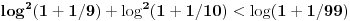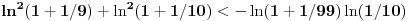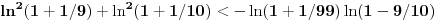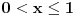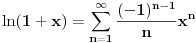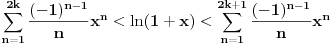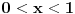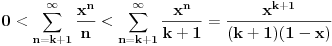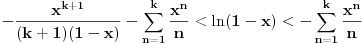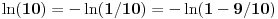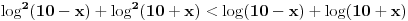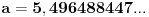[ miki069 @ 18.01.2025. 13:23 ] @
|
| Dokazati da je:
(log9)^2 + (log11)^2 > log(98)
Nemojte gubiti vreme i pokušavati da dokažete da je leva strana veća od log(99), jer nije veće, nego je manja od log(99).
Leva strana je za svega 0.0033.. veća od desne.
[Ovu poruku je menjao miki069 dana 18.01.2025. u 14:47 GMT+1] |
[ miki069 @ 19.01.2025. 10:46 ] @
Uputstvo:
(0.99)^2 = 0.9801 > 0.98
[ Nedeljko @ 19.01.2025. 18:30 ] @
[tex[(\log(9)-\log(11))^2>0[/tex]
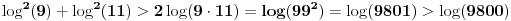 [ Nedeljko @ 20.01.2025. 02:11 ] @
Ovo iz nekog rayloga nisam mogao da ispravim.
Prvo, treba da se zna koja je osnova logaritma.
[ Trump Jr. @ 20.01.2025. 10:24 ] @
Osnova je zadata u prvom tekstu.
Dakle osnova je broj koji za tu razliku daje 0.0033..
Mada google digitron za tu razliku daje 0.00385141583
U toj prvoj nejednakosti zar nije trebalo biti
log2(9)+log2(11) = 2*log(9*11)
[ miki069 @ 20.01.2025. 10:44 ] @
Osnova logaritma je 10.
Dekadni logaritam.
Nedeljko je u pravu, jer u nekim knjigama pišu log(x), a misle na ln(x).
Tako da treba i to naglasiti, iako se podrazumeva.
Nejednakost koja stoji je:
(log9)^2 + (log11)^2 > 2*log(9)*log(11)
Ali ne vodi ka dokazu, jer 2*log(9)*log(11) nije veći od log(98), već je manji.
Još jedan hint:
9 = 10*0.9
11 = 10*1.1
[Ovu poruku je menjao miki069 dana 20.01.2025. u 13:43 GMT+1]
[ jans @ 20.01.2025. 13:18 ] @
Dokaz može i koriščenjem nejednakosti ( koja je ekvivalentna sa onom koju Miki navodi u napomeni ) 992=9801>9800.
[Ovu poruku je menjao jans dana 20.01.2025. u 14:33 GMT+1]
[ Trump Jr. @ 20.01.2025. 13:44 ] @
Citat: miki069
Osnova logaritma je 10.
Dekadni logaritam.
Nedeljko je u pravu, jer u nekim knjigama pišu log(x), a misle na ln(x).
Tako da treba i to naglasiti, iako se podrazumeva.
Nejednakost koja stoji je:
(log9)^2 + (log11)^2 > 2*log(9)*log(11)
Da, dobro, onda nemam pitanja.
[ miki069 @ 20.01.2025. 15:37 ] @
Možda je ostao neprimećen.
Još jedan hint:
9 = 10*0.9
11 = 10*1.1
Posle ide pravolinijski. Direktno.
[ Nedeljko @ 21.01.2025. 00:42 ] @
Imamo sledeći ekvivalencijski niz:
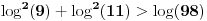 ,
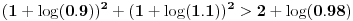 ,
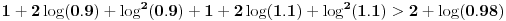 ,
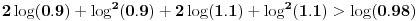 ,
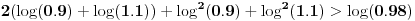 ,
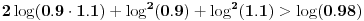 ,
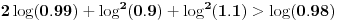 ,
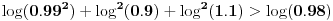 ,
 .
Prvi sabirak ne levoj strani je veći od desne strane, a preostala dva sabirka su pozitivna jer su kvadrati.
Pretpostavljam da se na ovo mislilo. [ jans @ 21.01.2025. 08:42 ] @
Može i ovako.
Logaritam broja 9 je manji, a logaritam broja 11 veći od jedinice, odnosno ti logaritmi nisu jednaki broju 1. Pošto kvadrat realnog broja koji nije nula mora da bude pozitivan, imamo
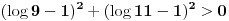
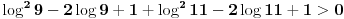
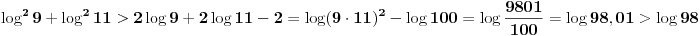 [ miki069 @ 21.01.2025. 10:47 ] @
Ovaj dugi dokaz je mnogo lepši.
Da li može da se dokaže da je:
(log9)^2 + (log11)^2 < log(99)
Leva strana je manja za svega 0.0005577...
[ Nedeljko @ 21.01.2025. 23:22 ] @
Može.
Numerička analiza služi upravo tome da se za dato  pronađe interval širine manje od  kome data vrednost pripada, što mora da obuhvata i dokaz pripadanja te vrednosti tom intervalu.
Takvi dokazi se temelje na istoj opštoj matematičkoj metodologiji na kojoj se zasniva cela matematika. Nema tu nikakve posebnosti numeričke analize. [ miki069 @ 22.01.2025. 18:49 ] @
Numerička analiza služi za približno rešavanje jednačina, određenih integrala, Košijevog problema...
Ne znam kako se ona koristi kod nejednačina?
[ Nedeljko @ 22.01.2025. 22:39 ] @
Dokažeš da se razlika leve i desne strane nejednakosti nalazi u nekom intervalu koji je levo od nule.
[ miki069 @ 22.01.2025. 23:08 ] @
Može hint?
Koju funkciju posmartam?
Šta dalje?
Možda sam nešta propustio iz Numeričke analize, a mislim da nisam.
Ili je u pitanju Tejlorov polinom funkcije f(x)=log(x) u okolini broja 10?
[ Nedeljko @ 23.01.2025. 00:38 ] @
Imamo ekvivalencijski niz
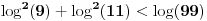 ,
 ,
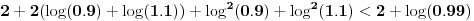
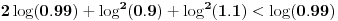
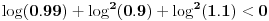
 ,
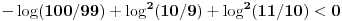 ,
 ,
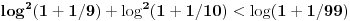 ,
 ,
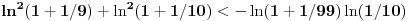 ,
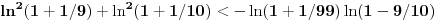 ,
Za 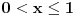 važi da je Maklorenov razvoj funkcije  alternativni red sa članovima koji su po apsolutnoj vrednosti sve manji. Dakle,
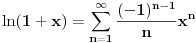 ,
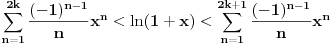 .
Za 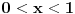 važi da je Maklorenov razvoj funkcije  red sa negativnim članovima. Dakle,
 .
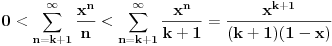 ,
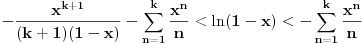 .
Ovo poslednje je za računanje 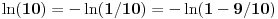 . [ miki069 @ 23.01.2025. 01:16 ] @
Na levoj strani nejednakosti su kvadrati od redova?
[ Nedeljko @ 23.01.2025. 03:31 ] @
Kvadrati donjih i gornjih granica vrednosti.
[ miki069 @ 23.01.2025. 12:50 ] @
Dupla nejednakost za nejednakosti za ln(1+x) mi je jasna, jer je u pitanju alternativni red.
Duplu nejednakost za ln(1-x) moram da ispišem, ali je najverovatnije tačna.
I kako posle biramo k?
[ miki069 @ 23.01.2025. 14:57 ] @
Da li bi ceo dokaz mogao jednostavnije, uz predhodni dokaz, da je:
log(9)*log(11) < 1 ?
Taj dokaz znam da izvedem.
[ Nedeljko @ 23.01.2025. 16:14 ] @
Biramo sve veće i veće k dok ne dobijemo interval za vrednost sa jedne strane nule, odakle zaključujemo da li je vrednost pozitivna ili negativna.
Dokaz za šta znaš da izvedeš?
[ miki069 @ 23.01.2025. 17:05 ] @
Znam da izvedem dokaz da je:
log(9)*log(11) < 1
Da li bi posle tog dokaza bio otvoren neki lakši put?
Samo glasno razmišljam.
Tvoje rešenje je OK, nego me zanima da li ima direktnije rešenje.
Bez Numeričke analize.
[Ovu poruku je menjao miki069 dana 23.01.2025. u 20:03 GMT+1]
[ jans @ 24.01.2025. 23:23 ] @
Pitanje za Mikija. Da li je druga nejednakost "tvoj" zadatak? Ako nije, možda je uz zadatak bilo i neko uputstvo za rešavanje, ili nagoveštaj da je zadatak moguće uraditi elementarno.
Zadatak može da se reši i tako što se, u skupu realnih pozitivnih brojeva, reši nejednačina ( odgovarajuća jednačina se reši numerički )
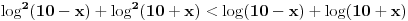 .
Jedan interval skupa rešenja je 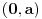 , gde je 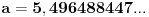 . Drugi interval koji sadrži brojeve suprotne brojevima iz prvog intervala, zbog simetrije izraza, ne daje nova rešenja. A pošto jedinica pripada navedenom intervalu, nejednakost je tačna, [ miki069 @ 25.01.2025. 00:04 ] @
Prva nejednakost je iz Krugove zbirke za II godinu.
Rešenje u zbirci je isto kao prvo rešenje koje je dao kolega Jans. Drugo rešenje je mnogo elegantnije.
Druga nejednakost nije iz zbirke.
Sam sam je primetio dok sam pokušavao da rešim prvu.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|