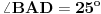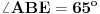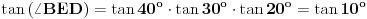[ jans @ 25.01.2025. 23:28 ] @
|
[ miki069 @ 30.01.2025. 18:21 ] @
Neka je tačka S presek duži AD i BE.
Ugao CAB = CBA = 80 stepeni. Ugao ASB=ESD=BSD=ASE=90 stepeni. EAD=55 stepeni. EBD=15 stepeni. BDS=75 stepeni. ADC=105 stepeni AES=35 stepeni BED+DEC=145 stepeni 90-BED + EDC = 105 stepeni 20 + DEC + EDC = 180 stepeni Ne znam kako dalje. [Ovu poruku je menjao miki069 dana 30.01.2025. u 20:12 GMT+1] [ jans @ 30.01.2025. 22:53 ] @
Rešio sam zadatak pomoću trigonometrije. Iskoristi pravougle trouglove sa zajedničkim temenom S.
Ne znam da li postoji drugi način rešavanja zadatka, odnosno da li može zadatak da se reši pomoću Euklidske geometrije. [ MajorFatal @ 30.01.2025. 23:12 ] @
Na slici broj jedan je data situacija sa svim trouglovima, i linijama, i poznatim uglovima, i onim koji nedostaju. Nije teško dodati liniju paralelnu osnovici l1 koja prolazi kroz tačku D, i istu takvu liniju l2 paralenu osnovici koja prolazi kroz tačku E. Takođe lako se odredi sredina duži DE, tačka F, i isto tako povuče simetrala te duži s. Tačka gde simetrala seče liniju l1 je obeležena sa G, a tačka gde simetrala s preseca liniju l2 je obeležena sa H.
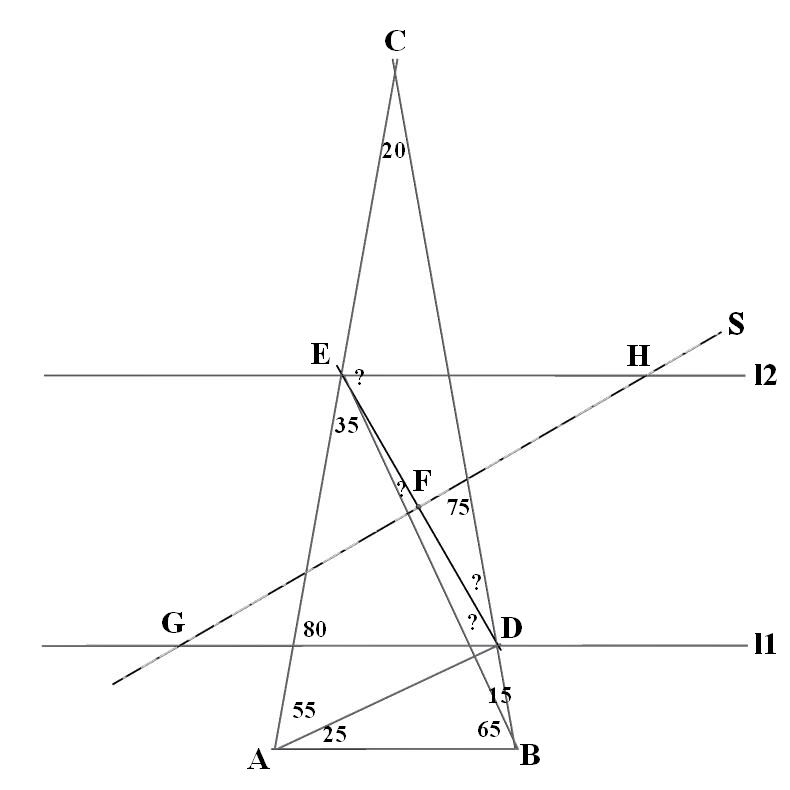 S obzirom da se tačka G nalazi na simetrali duži DE moguće je nacrtati kružnicu k1 sa centrom u tački G, a koja prolazi kroz obe tačke D i E, dužinu GD obeležimo sa malim a, jednaka je dužina od G do E pa i to obeležimo a, što će reći možemo smatrati da smo dobili jednakokraki trougao GDE sa uglom naspram osnovice alfa, i dva ugla beta na osnovici DE koja je za sada nepoznate dužine. Sve to isto iz tačke H, kružnica k2, i sa istim otvorom šestara, zbog sličnosti trouglova DGF sa EHF, ili zato jer linija s preseca dve paralelne linije l1 i l2. Trouglovi GDE i HED su isti samo različito orijentisani, te je kod H ugao alfa, a kod E i D ugao beta, ima dve stranice a, i kao osnovicu DE. Sve u svemu GDHE je romb, ali ne znamo dužinu manje dijagonale, niti unutrašnje uglove. 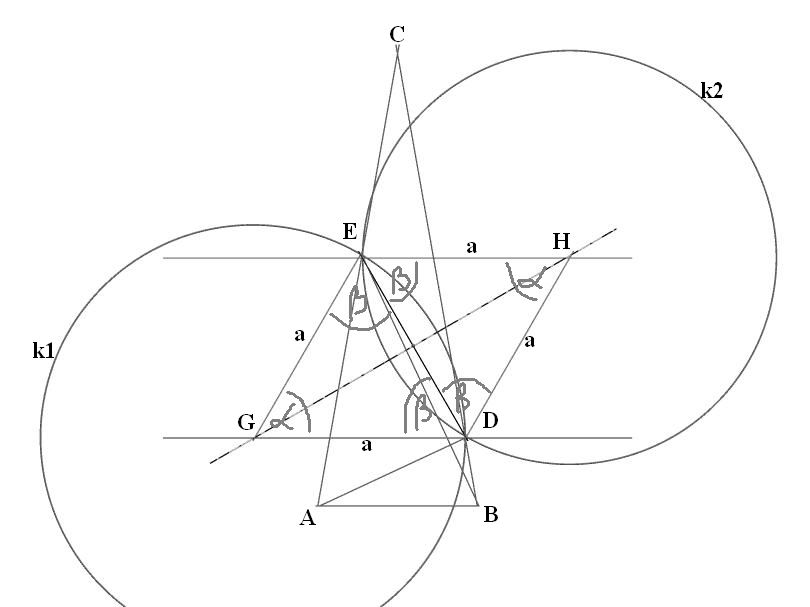 [ MajorFatal @ 30.01.2025. 23:36 ] @
Te sledi rasplet: dodajemo još jednu kružnicu k3, sa istim otvorom šestara, sa centrom u tački D, tačka D je podjednako, za dužinu a udaljena od G i od H, tako da kružnica može da prođe kroz obe te tačke. Za tačku E za sada ne znamo, jer ne znamo rastojanje od D do E, pa bi kružnica k3 mogla da prođe ispod ili iznad tačke E, ali ima nešto što može da pomogne: Kružnica k3 takođe preseca na još jednom mestu liniju l1 i tu tačku smo obeležili sa I, rastojanje od D do I je takođe a, tj. poluprečnik kružnice, i nalazi se na istoj pravi l1 a koja je paralelna sa l2, na kojoj se opet nalazi duž EH koja je isto dužine a.
Kako su H i I udaljeni za jednak iznos na paralelnim pravama, to je duž HI paralelna duži DE. Kružnice k2 i k3 sa centrima u H i D su u takvom odnosu da je centar jedne na liniji kružnice druge, pa je tu moguće konstruisati dva jednakostranična trougla, ili romb sastavljen od dva takva trougla, a kome je manja dijagonala duž HD. Sledi da je i dužina HI jednako malo a, te da kružnica k3 sasvim sigurno prolazi kroz tačku E, koja već pripada kružnici k2, koja je tako i konstruisana da prođe kroz tačku E. Sledi da je dužina DE takođe malo a, te da zaklapa ugao od 60 stepeni u odnosu na osnovicu AB, tj paralelne linije l1 i l2. A pošto BE zaklapa sa osnovicom ugao od 65 stepeni, razlika ta dva ugla je 5 stepeni. 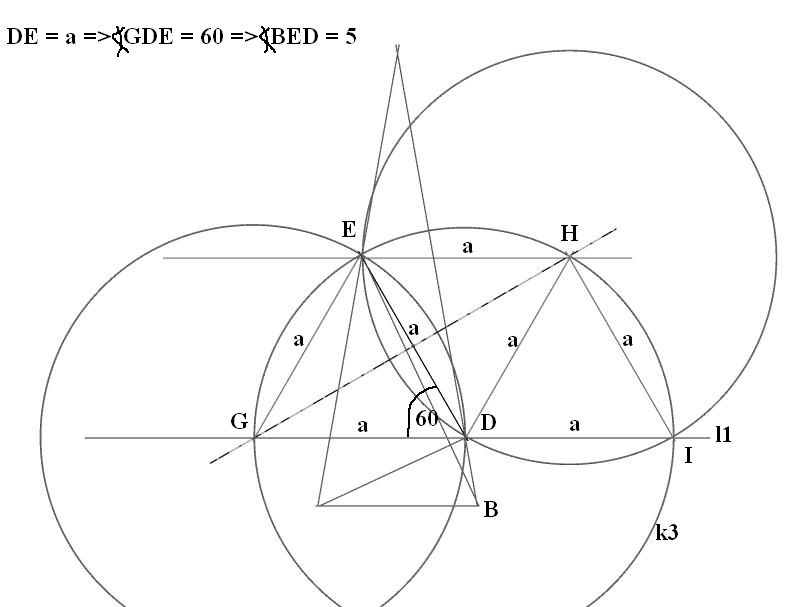 [ jans @ 31.01.2025. 22:58 ] @
Citat: MajorFatal: Kako su H i I udaljeni za jednak iznos na paralelnim pravama, to je duž HI paralelna duži DE. Kružnice k2 i k3 sa centrima u H i D su u takvom odnosu da je centar jedne na liniji kružnice druge, pa je tu moguće konstruisati dva jednakostranična trougla, ili romb sastavljen od dva takva trougla, a kome je manja dijagonala duž HD. Sledi da je i dužina HI jednako malo a, te da kružnica k3 sasvim sigurno prolazi kroz tačku E, koja već pripada kružnici k2, koja je tako i konstruisana da prođe kroz tačku E. U navedenom postupku, nepoznati ugao je izračunat pomoću ugla  , koji ima meru 600, pošto je, prema tvom tvrđenju, dijagonala romba - duž ED, jednaka duži a. , koji ima meru 600, pošto je, prema tvom tvrđenju, dijagonala romba - duž ED, jednaka duži a. Da li si siguran da je citirani deo, dobro obrazloženje za tvrđenje da je ED=a? Ja mislim ( i bez provere logičke ispravnosti citiranog dela) da nije, zato što je zaključak izveden iz pretpostavke da se tačke I i J poklapaju ( na priloženoj slici tačka J je presečna tačka kružnice k2 i prave l1; napominjem da na slici nisu nacrtani elementi koji nisu neophodni za ovo moje objašnjavanje, a kružnica k1 koja je u navedenom postupku suvišna, nacrtana isprekidanom linijom ). 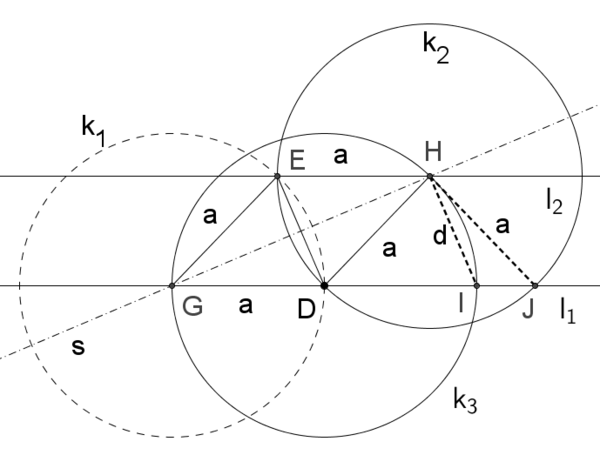 Međutim te tačke ne moraju da budu identične. One će se poklopiti ako i samo ako kružnica k3 sadrži tačku E. Ti si dobro uočio da kružnica k3 ne mora da prolazi kroz tačku E, ali nisi bio dosledan i prevideo si činjenicu da ni tačke I i J ne moraju da se poklapaju. Pošto si, prema postavci zadatka, jednakokraki trougao precizno konstruisao ( ako na toj slici izmeriš nepoznati ugao, njegova mera će biti 5o ), na toj slici tačke I i J moraju biti identične, pa te slika "navela" da načiniš previd. [ MajorFatal @ 01.02.2025. 00:06 ] @
Slažem se u potpunosti mr Jans, previd, propust, sam primetio još popodne, ali celo veče sam bio zauzet, a sad kad sam seo da ispišem ispravku sačekao me vaš komentar. Samo ću ostatak rešenja ispisati svojim rečima, kako umem i znam, i dodao bih da nije fer od vas da mi poturate tačku J kad lepo mogu da se uoče tačke M i N :)
Dakle, isto kao što kružnica k3 može da omaši tačku E u jednom delu rešenja, ni jednom rečju nisam spomenuo zašto bi kružnica k2 prošla baš kroz tačku I, jans je u pravu, zaveo me softver kojim sam crtao, koji je sve lepo smestio gde treba, kružnica i prolazi tuda, i konstrukcija koju sam predložio jeste takva, ali treba pokazati zašto i kako. Za kružnicu k2 znamo zasigurno da prolazi kroz D i E, ali bi mogla da omaši tačku I, te linije l1 i kružnicu k3 preseče u nekim drugim tačkama. Smatram da je dokazivanje da k2 prolazi baš kroz I i tu seče kružnicu k3 manje više jednostavno: Ako uočimo tačke gde se te dve kružnice seku međusobno, a ja sam ih obeležio M i N, to su tačke koje pripadaju rombu, ili dva jednokostranična trougla. Ali za razliku od romba GDHE kod koga smo znali stranice, ali ne i i manju dijagonalu i uglove, u slučaju romba MDNH znamo kraću dijagonalu DH da je jednaka a, te da je pravilan, ima uglove 60 i 120, te da su i sve stranice takođe jednake a. Kako je rastojanje DI takođe jednako a, znamo da identičan romb HIDE mora da postoji na za to odgovarajućem mestu. Odnosno ovde ima i jedna mala zanimljivost da tako kaže čovek, za pokazivanje da je romb baš na tom mestu može da posluži duž DI, ali ne i duž HI, to jest HJ koju je jans nacrtao i tako ljubazno obeležio sa dužinom a, i poturio meni da me zavede. Naime DI u tom trenutku rešenja ima sebi paralelnu duž EH, dok HI nema, zapravo u jednom kasnijem koraku crtamo HI i zaključujemo da je paralelna ED na osnovu toga što pripadaju istom pravilnom rombu ... Da pokušam da se izrazim najpreciznije moguće što umem: Ukoliko bi postojala tačka M i bila izvan linije l1, i predstavljala presek kružnica k1 i k2, u tom slučaju rastojanje DM bi iznosilo a, jer ta tačka je na kružnici pa je rastojanje jednako poluprečniku te kružnice. Međutim znamo i da je kružnica k3 negde presekla liniju l1, i tu tačku smo nazvali I i rastojanje do nje je takođe a. Pride duž DI ima sebi paralenu duž EH koja je takođe dužine a. I evo zakucah ... mislio sam da može kraće i jednostavnije ... a ne crta mi se simetrala DH nit mi se konstruiše još jedna kružnica .. Da li bi se ovo uvažilo preko tačke J: Tačka J se ne može nalaziti dalje od tačke I u odnosu na tačku D, jer je DI već određeno da je dužine a, prema tome tačka J se ne može nalaziti desno na crtežu od tačke I, jer ne mogu da postoje dve različite dužine a, a udaljenost DJ bi takođe morala biti a, zbog toga što je DJ, po ovakvoj konstrukciji, deo pravilnog romba sa svim stranicama a. Prema tome kružnica k2 mora preseći liniju l1 i kružnicu k3 samo u tački I i nigde drugde ... ostalo sleduje iz prethodno navedenog ... da ne ponavljam ... ugao DIH je 60 jer je deo romba itd ... 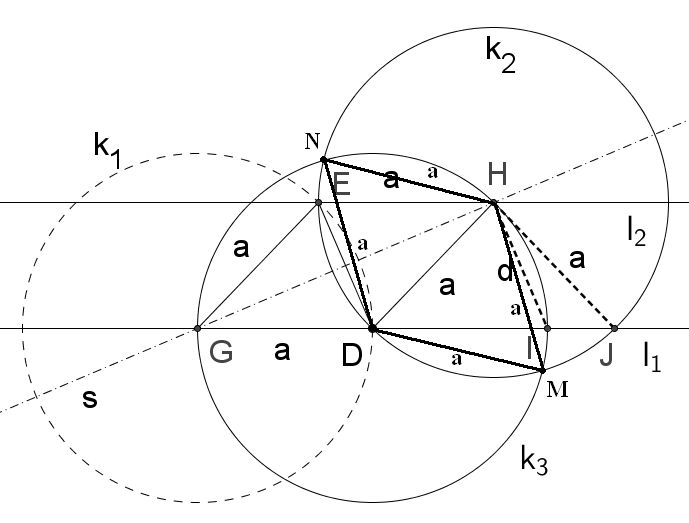 [ MajorFatal @ 01.02.2025. 07:56 ] @
Odnosno da probam da uopštim i pomenem i tačku M, pošto za nju ne važe ista pravila kao za J, koja bi se nalazila na liniji l1, pa bila lakša za merenje.
Jer DM stvarno iznosi a, dok za HM iz onog do tada predstavljenog ne možemo znati da ne iznosi baš a, pod tim uglom i nepoznatom razdaljinom: Ako bi kružnica k2 prolazila bilo gde mimo tačke I, u tom slučaju ona bi presekla liniju l1 i kružnicu k3 u dve različite tačke, nazvaćemo ih J i M. U jednom slučaju ti preseci bi bili desno i ispod tačke I, u drugom slučaju levo i iznad I. Ali u oba takva slučaja dimenzija DJ ne bi odgovarala dužini a, koja je ranije utvrđena i nalazi se na potezu DI, prema tome takve konstrukcije su nemoguće, tačka J mora da se nalazi na mestu I, a samim tim i tačka M. To jest to je sve jedna jedinstvena tačka I. [ miki069 @ 01.02.2025. 21:07 ] @
Majore, zar nije jednostavnije da se dokaže da je EC=ED?
[ MajorFatal @ 02.02.2025. 00:35 ] @
Ako je jednostavnije, samo napred, dokaži.
Ja znam da je EC = ED, ali ne umem to da dokažem, nit umem to da primenim u računanju ugla između DE i BE. [ MajorFatal @ 02.02.2025. 07:55 ] @
U stvari .. izvini .. zapetljano pa trokiram svaki čas .. mislio sam da znam da je ED = EC jer sam dok sam rešavao crtao i kružnicu iz E pa znam da prolazi kroz C, ali to znam isto preko crteža, a u stvari takva kružnica prolazi zasigurno kroz H i G, a za D i C bi moralo da se dokazuje da prolazi baš tuda ..
A realno situacija je, ako bi mi neko potvrdio da sam ovo do sada dobro rešio :) zbog nagiba u odnosu na osnovicu ED 60, i CD 80, znam da je ugao CDE 20 stepeni, tj da je trougao CDE jednakokraki sa uglovima 20 20 140, te tako mogu da dokažem da je ED = EC, ali to je jasno tek pošto sam ispisao sve ovo do sad, pa mi za rešenje koliko je ugao BED mnogo ne znači .. [ miki069 @ 02.02.2025. 15:08 ] @
Šalim se Majore.
Ja ne uspevam ni preko trigonometrije, a moralo bi da može. Previše nepoznatih. [ jans @ 02.02.2025. 17:29 ] @
Citat: MajorFatal: .... i dodao bih da nije fer od vas da mi poturate tačku J kad lepo mogu da se uoče tačke M i N :) ..... Odnosno ovde ima i jedna mala zanimljivost da tako kaže čovek, za pokazivanje da je romb baš na tom mestu može da posluži duž DI, ali ne i duž HI, to jest HJ koju je jans nacrtao i tako ljubazno obeležio sa dužinom a, i poturio meni da me zavede. Najpre da napomenem da, kada pišem neku poruku ili komentar na postove u nekoj temi, vodim računa o Pravilniku foruma, posebno o tački 4, odnosno i o tački 12. Smatram da u mojoj prethodnoj poruci u ovoj temi ništa nije u suprotnosti sa Pravilnikom foruma, takođe da ništa nisam samouvereno tvrdio, niti sam bio ciničan. Nisam ništa poturio sa namerom da „zavedem“. Samo sam na primeren način ukazao na (neke) propuste u porukama člana MajorFatal. Što se tiče tačaka M i N, tih tačaka u porukama koje sam komentarisao nije bilo. Zašto ja treba da ih uočim? Uočio sam tačku J pa konstruisao duž HJ i obeležavanjem napomenuo da je njena dužina a, a sve to da bi istakao da je ta duž duža od duži d, odnosno dijagonale romba ED. A sada još jednom o prethodnom postupku. Kroz tačke D i E konstruisane su paralele l1 i l2 (paralelne sa osnovicom trougla). Zatim je konstruisana simetrala duži DE koja paralele seče u tačkama G i H. Četvorougao GEHD je romb. Stranica romba je obeležena slovom a, a ugao između stranice romba i dijagonale DE obeležen sa  . Na priloženoj slici nije trougao sa uglovima i duž BE, zato što se ti objekti ne koriste u navedenom postupku. Eventualno bi mogli konstruisati i duž BE, koja osnovicu romba seče pod uglom od 65o, ali se ona ne može iskoristiti u dokazivanju. Na osnovu položaja te duži na jednoj od prethodnih slika, možemo zaključiti da je . Na priloženoj slici nije trougao sa uglovima i duž BE, zato što se ti objekti ne koriste u navedenom postupku. Eventualno bi mogli konstruisati i duž BE, koja osnovicu romba seče pod uglom od 65o, ali se ona ne može iskoristiti u dokazivanju. Na osnovu položaja te duži na jednoj od prethodnih slika, možemo zaključiti da je 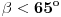 . .Pošto nemamo drugih podataka o rombu, nije moguće odrediti ugao  (možemo ga samo izmeriti), niti možemo dokazati da taj ugao ima određenu meru (ako smo prethnodno veličinu ugla odredili merenjem), odnosno nije moguće utvrditi (ili dokazati) da li su stranica romba i dijagonala DE jednake ili različitih dužina. (možemo ga samo izmeriti), niti možemo dokazati da taj ugao ima određenu meru (ako smo prethnodno veličinu ugla odredili merenjem), odnosno nije moguće utvrditi (ili dokazati) da li su stranica romba i dijagonala DE jednake ili različitih dužina.Prema tome, samo pomoću navedenih paralela, odnosno romba, zadatak nije moguće rešiti. Kružnice k3 i k2, ne menjaju situaciju zato što ne "sadrže" nikakav podatak o rombu (izuzev stranice romba). [Ovu poruku je menjao jans dana 02.02.2025. u 19:50 GMT+1] [ miki069 @ 03.02.2025. 06:05 ] @
Ako bi tačku E pomerili malo bliže tački A, toliko da se ugao od 65 stepeni promeni u 60 stepeni i
tačku D pomerili bliže tački C, tako da se ugao od 25 stepeni promeni u 30 stepeni, da li bi ugao BED i dalje bio 5 stepeni? [ MajorFatal @ 03.02.2025. 11:38 ] @
To niko ne zna :) šalim se .. i ja sam primetio da je razlika po 5 stepeni do okruglih uglova 30 i 60, pa pokušavao da rotiram trougao sa tvojim oznakama SED, međutim čas seče ovde, čas onde, produžava se, skraćuje, na kraju odustao ..
[ jans @ 03.02.2025. 19:22 ] @
Ako bi pomerili tačke D i E, odnosno sa uglovima 30o i 60o, mera nepoznatog ugla bi bila 10o.
[ miki069 @ 03.02.2025. 20:45 ] @
Hvala Jans.
Sutra se upuštam u trigonometriju. [ MajorFatal @ 04.02.2025. 23:08 ] @
Citat: jans: Najpre da napomenem da, kada pišem neku poruku ili komentar na postove u nekoj temi, vodim računa o Pravilniku foruma, posebno o tački 4, odnosno i o tački 12. Smatram da u mojoj prethodnoj poruci u ovoj temi ništa nije u suprotnosti sa Pravilnikom foruma, takođe da ništa nisam samouvereno tvrdio, niti sam bio ciničan. Nisam ništa poturio sa namerom da „zavedem“. Samo sam na primeren način ukazao na (neke) propuste u porukama člana MajorFatal. Ma znam Mr jans, šalim se, nisam nikako mogao da sročim obrazloženje za svoju konstrukciju pa sam brbljao ne bi li me strefila neka iskra inspiracije, koncentracije, ili obrazloženog opravdanja, ne obraćajte pažnju. Citat: Uočio sam tačku J pa konstruisao duž HJ i obeležavanjem napomenuo da je njena dužina a, a sve to da bi istakao da je ta duž duža od duži d, odnosno dijagonale romba ED. Ovde ipak moram malo da se pobunim, sve što ste napisali važi za ovakav pokrivljen crtež, vi ste ga pokrivili da bi ilustrovali nešto a to je da k3 može da ne prolazi kroz tačke E i J. To nije sporno. Sporno je da ste mogli da pokrivite crtež i na drugi način, tad bi k3 prošla ispod tačke E na primer, a tačka preseka k3 i l1 koju sam nazvao I bi završila desno na crtežu u odnosu na tačku J na primer. U tom slučaju ne bi istakli da je HJ "duža" od dijagonale romba d, već da je "kraća". Jednom rečju slažem se da ste pokazali da HJ ne mora da bude na ovakav način crtana jednake dužine kao d, ali ne slažem se da je "duža". Citat: A sada još jednom o prethodnom postupku. Kroz tačke D i E konstruisane su paralele l1 i l2 (paralelne sa osnovicom trougla). Zatim je konstruisana simetrala duži DE koja paralele seče u tačkama G i H. Četvorougao GEHD je romb. Stranica romba je obeležena slovom a, a ugao između stranice romba i dijagonale DE obeležen sa  . Na priloženoj slici nije trougao sa uglovima i duž BE, zato što se ti objekti ne koriste u navedenom postupku. Eventualno bi mogli konstruisati i duž BE, koja osnovicu romba seče pod uglom od 65o, ali se ona ne može iskoristiti u dokazivanju. Na osnovu položaja te duži na jednoj od prethodnih slika, možemo zaključiti da je . Na priloženoj slici nije trougao sa uglovima i duž BE, zato što se ti objekti ne koriste u navedenom postupku. Eventualno bi mogli konstruisati i duž BE, koja osnovicu romba seče pod uglom od 65o, ali se ona ne može iskoristiti u dokazivanju. Na osnovu položaja te duži na jednoj od prethodnih slika, možemo zaključiti da je 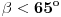 . .Pošto nemamo drugih podataka o rombu, nije moguće odrediti ugao  (možemo ga samo izmeriti), niti možemo dokazati da taj ugao ima određenu meru (ako smo prethnodno veličinu ugla odredili merenjem), odnosno nije moguće utvrditi (ili dokazati) da li su stranica romba i dijagonala DE jednake ili različitih dužina. (možemo ga samo izmeriti), niti možemo dokazati da taj ugao ima određenu meru (ako smo prethnodno veličinu ugla odredili merenjem), odnosno nije moguće utvrditi (ili dokazati) da li su stranica romba i dijagonala DE jednake ili različitih dužina.Prema tome, samo pomoću navedenih paralela, odnosno romba, zadatak nije moguće rešiti. Kružnice k3 i k2, ne menjaju situaciju zato što ne "sadrže" nikakav podatak o rombu (izuzev stranice romba). Slažem se, trenutno ne mogu da smislim zašto bi kružnica k3 morala da prođe i kroz E i kroz J da bi čitava konstrukcija postojala. [ miki069 @ 06.02.2025. 16:15 ] @
Iz prvouglih trouglova se vrlo lako dobija da je:
tg(BED) = tg(15o)*t(25o)/tg(55o). Treba se dokaže da je to tg(5o). Lako se dokaže preko adicionih formula da: ako je tg(alfa)=t, onda je tg(3*alfa) = (3*t-t^3)/(1-3*t^2). 15 iskaže kao 3*5 stepeni, 25 kao 30-5 i 55 kao 60-5. Detaljan račun je u prilogu. [Ovu poruku je menjao miki069 dana 06.02.2025. u 17:54 GMT+1] [ jans @ 06.02.2025. 23:20 ] @
Iz rešenja koje je izložio Miki možemo dobiti zanimljivu relaciju.
Pošto je 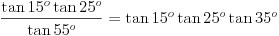 , sledi da je , sledi da je 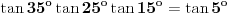 . .Ako umesto funkcije tangens odredimo kotangens traženog ugla dobićemo da je 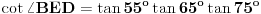 , pa imamo još jednu interesantnu jednakost , pa imamo još jednu interesantnu jednakost 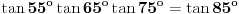 . . Poslednju jednakost možemo dokazati i pomoću formula za pretvaranje proizvoda trigonometrijskih fnkcija u zbir. [ MajorFatal @ 07.02.2025. 15:07 ] @
Citat: miki069: Ako bi tačku E pomerili malo bliže tački A, toliko da se ugao od 65 stepeni promeni u 60 stepeni i tačku D pomerili bliže tački C, tako da se ugao od 25 stepeni promeni u 30 stepeni, da li bi ugao BED i dalje bio 5 stepeni? Meni bilo zanimljivo ovo pomeranje tački, pa sam pošao od pozicije gde je ugao BED poznat i iznosi 25 stepeni, i kad se tačka E pomera po liniji AC do pozicije E' ponaša se po nekom pravilu: 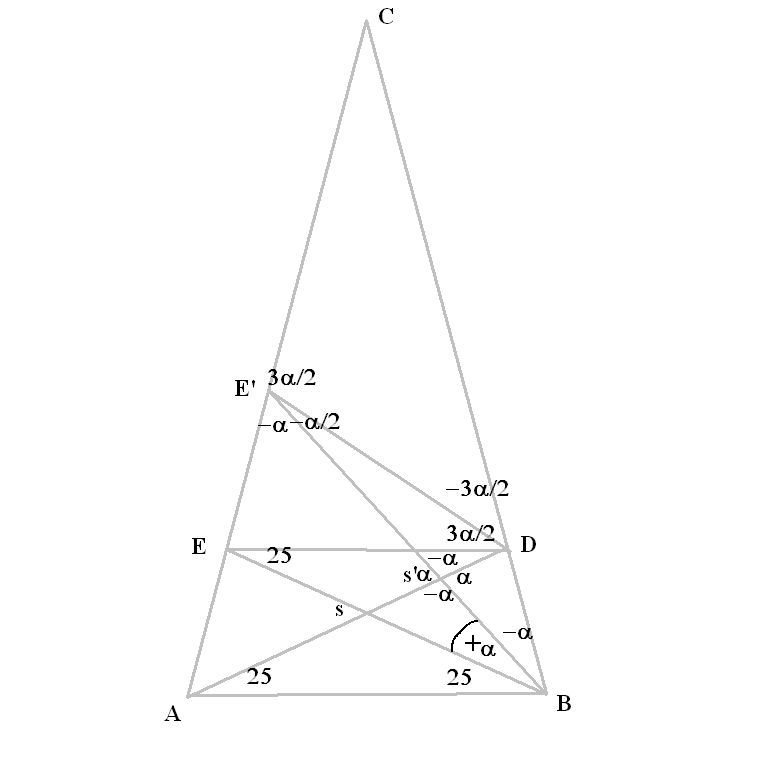 Dakle ako tačka E promeni poziciju i postane E' ugao ABS se poveća na ABS' za neki nepoznat iznos alfa. Jasno za koliko se ABS' povećao za toliko mora da se smanji njemu spoljni SBC to jest za minus alfa. Slično u trouglu AS'B zbir uglova mora ostati konstantan, a kako je ugao S'AB ostao nepromenjen, ako se ABS povećao za alfa i postao ABS', za toliko se umanji treći ugao trougla tj ugao AS'B će biti za minus alfa manji od originalnog ASB. Sve isto u trouglu ABE to jest ABE', ugao AE'B ća za minus alfa biti manji u odnosu na originalni AEB. Uglovi AS'B i DS'E' su unakrsni i jednaki, pa će DS'E' da se umanji za iznos alfa, njima dodatni uglovi do punog ugla BS'D i E'S'A unakrsni i jednaki će se povećati za iznos alfa. I sve ovo do sad je manje više jasno, i da ne kažem logično. Sledi deo koji meni nije jasan ... U trouglu ESD kad postane E'SD ugao kod S' se umanjio za iznos alfa, pa bi preostala dva ugla u trouglu E'S'D morali to da nadoknade da bi zbir sva tri ugla u trouglu bio 180. Iz nekog razloga to se dešava po pravilu da se S'E'D (ili BE'D koji se traži u zadatku) umanjuje za alfa pola, a preostali ugao trougla E'DS' povećava za 3 alfa polovine? Kad se E'DS' poveća za 3 alfa polovine, njemu spoljni E'DC se smanji za isti iznos, kako zbir uglova i u trouglu E'DC mora ostati konstantan, DE'C se poveća za 3 alfa polovina. Moje pitanje je zašto baš ovi iznosi alfa pola, i 3 alfa pola? Proverio sam na par drugih primera i za njih ne važi takvo pravilo. U stvari ne važi ni u ovoj konstrukciji uvek, deluje da su 25 i 65 za duž BE granični uglovi za koje ovo pravilo važi? Kad bih ovako polazeći od poznatog ugla pokušao da otkrijem koliko je BED računica se slaže, od 25 do 65 dodato je alfa = 40 stepeni, ugao BED je jednako početni minus alfa pola, sledi 25 - 20 = 5 stepeni .. [ miki069 @ 08.02.2025. 17:44 ] @
Citat: jans: Ako bi pomerili tačke D i E, odnosno sa uglovima 30o i 60o, mera nepoznatog ugla bi bila 10o. Meni u tom slučaju ispada 6.9... stepeni. [ jans @ 08.02.2025. 22:15 ] @
[ miki069 @ 09.02.2025. 09:37 ] @
U pravu si Jans.
Tada je ugao 10 stepeni. Pokušavam bez trigonometrije, ali neće nikako. Nije mi jasno kako je Deep Seek toliko pogrešio u originalnom zadatku? Đoka je napisao njegov račun u temi jednakostranični trougao. [ jans @ 10.02.2025. 00:34 ] @
Citat: miki069: „Nije mi jasno kako je Deep Seek toliko pogrešio u originalnom zadatku?“ Verovatno je problem granica greške. U navedenom postupku izračunavanja se vrše pomoću približnih vrednosti koje su zaokružene na četiri decimalne cifre. Taj postupak ima mnogo koraka u kojima se računa sa približnim vrednostima, a verovatno se u svakom od tih koraka granica greške poveća. Trebalo bi u računanju koristiti „preciznije“ vrednosti,odnosno računati sa više decimalnih cifara ( kalkulator koji koristim, vrednosti trigonometrijskih funkcija računa sa devet decimalnih cifara ). A sada još malo o zadatku. Zadatak možemo rešiti u opštijem obliku. Neka je 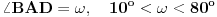 , a , a 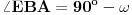 ( pošto su duži AD i BE normalne ). Presek duži AD i BE obeležimo sa F. Pošto su trouglovi određeni sa dužima AD i BE, i njihovim krajnjim tačkama, pravougli, a uglovi na osnovici jednakokrakog trougla, sa merom 80o, jednostavno možemo izraziti pomoću ugla ( pošto su duži AD i BE normalne ). Presek duži AD i BE obeležimo sa F. Pošto su trouglovi određeni sa dužima AD i BE, i njihovim krajnjim tačkama, pravougli, a uglovi na osnovici jednakokrakog trougla, sa merom 80o, jednostavno možemo izraziti pomoću ugla  , na slici istaknute uglove. , na slici istaknute uglove.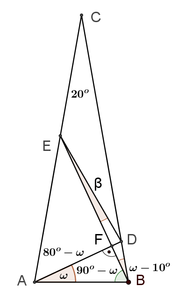 Pošto u navedenim pravouglim trouglovima primenimo definicije trigonometrijskih funkcija dobijamo naredne jednakosti 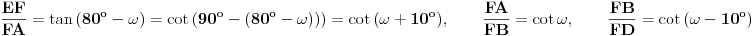 Množenjem ovih jednakosti dobijamo 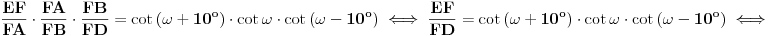 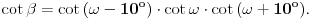 Koristeći ovu formulu možemo odrediti za koje celobrojne vrednosti ugla  , i ugao , i ugao  ima celobrojnu vrednost. ima celobrojnu vrednost.Ako je 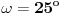 , biće , biće 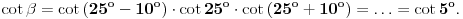 Ako je 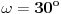 , biće , biće 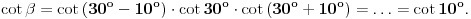  [Ovu poruku je menjao jans dana 10.02.2025. u 07:23 GMT+1] [ miki069 @ 10.02.2025. 19:17 ] @
Majore, a mogu i ostali, mada on najbrže crta.
Neka S bude oznaka za teme 4 prava ugla, to jest presek duži EB i AD. Normala iz tačke D na duž AC je seče u tački F. Normala iz tačke E na duž BC je seče u tački G. Kružnica opisana oko trougla ESD sadrži i tačke F i G. Ako on ne reši zadatak, više ideja nemam. Nemam dobru sliku. [ MajorFatal @ 10.02.2025. 21:19 ] @
Odavno ne čuh bolji vic, no šta da radim, ako najbrže crtam da zasučem rukave .. :) samo moram da te upozorim da su moji crteži skice, uglovi su dobri, nekad i veličine kružnica, ali tačke odakle kreću liniju često nisu, pa je crtež samo zbir nagađanja, kao što reče jans vredi koristiti geogebru, ali u njoj onda treba znati i raditi .. no šta je tu je, crtež je tu, ako je pitanje bilo da li kružnica prolazi kroz one tačke odgovor je - verovatno .. ali treba i dokazati nekako jelte .. edit: još ćeš mi reći da se GE i DF seku pod uglom od 20 stepeni? :) ..
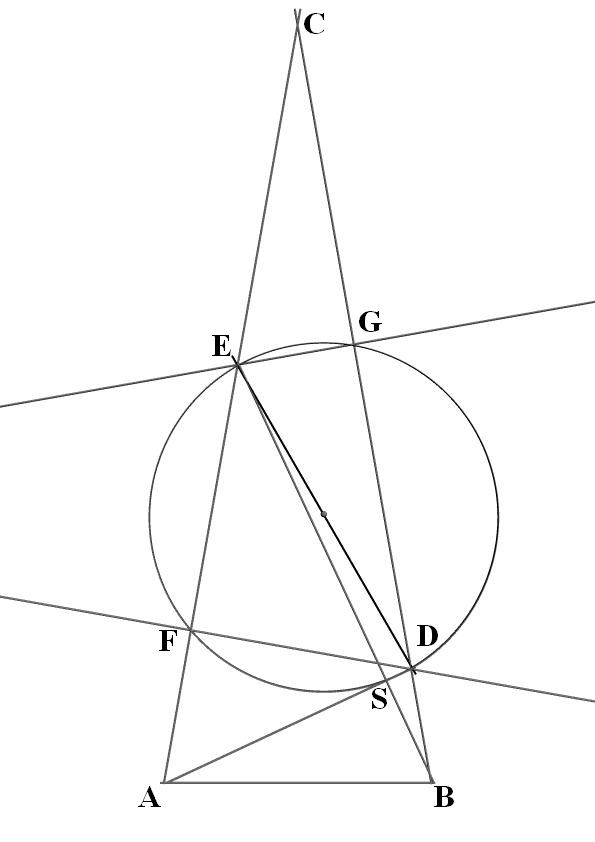 [ miki069 @ 11.02.2025. 06:06 ] @
Hvala na slici.
Kružnica prolazi kroz svih pet tačaka: D, E, F, G i S, zbog toga što su trouglovi: ESD, EFD i EGD pravougli sa zajedničkom hipotenuzom ED. [Ovu poruku je menjao miki069 dana 11.02.2025. u 07:29 GMT+1] [ MajorFatal @ 11.02.2025. 16:10 ] @
Nema na čemu, ali ako čitaš sa slike nije dobro, ako prvo povučeš normale, moraš da dokažeš da kružnica prolazi baš kroz G i H. Ako prvo nacrtaš kružnicu koja u nekim tačkama preseca AC i BC, onda moraš da dokažeš da se normale spuštaju baš u te tačke ...
Što će reći evo drugi crtež, kružnica je (kao) prošla kroz E,D,S ali nije kroz G i H ... 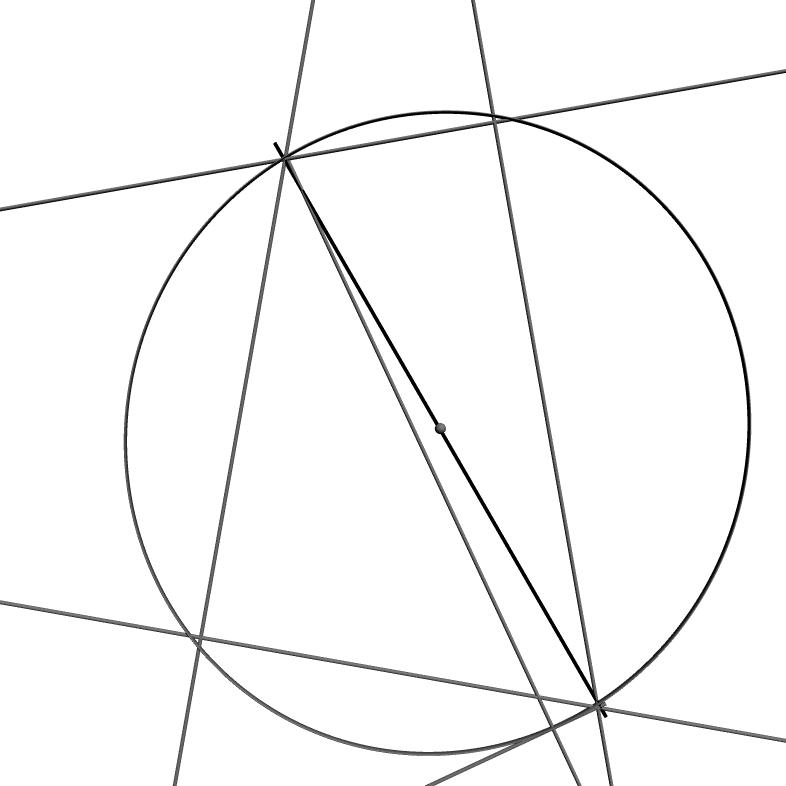 [Ovu poruku je menjao MajorFatal dana 11.02.2025. u 17:25 GMT+1] [ miki069 @ 11.02.2025. 16:47 ] @
Majore možda ti je promaklo da su sva tri trougla ESD, EFD i EGD pravougli, sa istom hipotenuzom ED.
Centar opisane kružnice za bilo koji od ova tri trougla je središte duži ED, a poluprečnik ED/2. Isti centar, isti poluprečnik, sledi po definiciji kružnice da je to jedna te ista kružnica. Na brzinu ne dobijam ništa. Čak ne pomaže ni potencija tačke u odnosu na kružnicu. GE i DF seku pod uglom od 20 stepeni. Uglovi sa normalnim kracima. Nisam probavao potenciju sa te strane. [ MajorFatal @ 12.02.2025. 08:47 ] @
Ma nije mi promaklo, nego se svaki čas predomišljam šta jeste, šta nije, a ovaj put jeste, mislim da si u pravu, i takođe ne znam kako dalje do ugla BED ,,
[ jans @ 16.02.2025. 17:44 ] @
Još jednom napominjem da mi nije poznato da li može zadatak da se reši pomoću Euklidske geometrije.
Ako neko zna odgovor, bilo bi korisno za posetioce foruma koji žele, odnosno pokušavaju da reše zadatak, da to napiše u poruci ( ako je odgovor potvrdan, nije neophodno da napiše to rešenje ). [ miki069 @ 04.04.2025. 17:25 ] @
Ako je zadatak nerešiv primenom Euklidske geometrije, trebalo bi moderatori da ga prebace u temu Nerešni zadaci sa ovog foruma.
[ Nedeljko @ 05.04.2025. 07:33 ] @
[ miki069 @ 06.04.2025. 15:43 ] @
Nisu isti zadaci.
[ Nedeljko @ 06.04.2025. 21:02 ] @
Pa, takve teoreme omogućavaju da se svako reššenje zadatka trigonometrijom transformiše u rešenje euklidskom geometrijom, jer trigonometrija proističe iz euklidske geometrije.
Dakle, sve što je rešivo trigonometrijom je rešivo euklidskom geometrijom. Druga je stvar što je takvo dobijeno rešenje euklidskom geometrijom duže i složenije od rešenja trigonometrijom. Prema tome, pitanje da li je rešivo euklidskom geometrijom ima trivijalan potvrdan odgovor. Druga je stvar da li postoji i neko kraće i elegantnije rešenje euklidskom geometrijom. Ako je odgvor negativan, onda je to primer koji opravdava postojanje trigonometrije jer olakšava rešavanje nekih zadataka. [ miki069 @ 07.04.2025. 17:06 ] @
Nedeljko jasno je da važi stav:
Ako je zadatak rešiv Euklidskom geometrijom sigurno je rešiv i trigonometrijom. Nisam siguran da važi i obrnuto. Problem je što je ugao od 5o trećina ugla od 15o. A ne može se konstruisati, jer je nemoguća konstrukcija ugla od 20o. Ugao od 15o se može konstruisati kao polovina od 30o. [ jans @ 07.04.2025. 23:29 ] @
U ovom primeru određivanje nepoznatog ugla nije moguće svesti samo na primenu osobina mnogougla ( zbir unutrašnjih uglova, ... ). Rešavanje zadatka pomoću Euklidske geometrije podrazumeva da treba da dokažemo da je taj ugao ( ili ugao koji u sebi sadrži nepoznati ugao ), jednak uglu sa poznatom merom ( uglu koji smo na neki način uočili, ili smo ga "konstruisali" ). Tu jednakost dokazujemo pomoću podudarnih ili sličnih trouglova, ili koristeći uglove sa paralelnim ( ili sa normalnim ) kracima. Jednakost uglova ( i duži ) ne dokazujemo konstrukcijom. Nije bitno da li je moguće konstruisati neki ugao, odnosno kako je taj ugao konstruisan. ( I u zadatku imamo uglove koje, pomoću lenjira i šestara, nije moguće konstruisati. )
[ Nedeljko @ 08.04.2025. 09:29 ] @
Citat: miki069: Nedeljko jasno je da važi stav: Ako je zadatak rešiv Euklidskom geometrijom sigurno je rešiv i trigonometrijom. Nisam siguran da važi i obrnuto. Pa, to obrnuto je trivijalno jer je trigonometrija specijalan slučaj euklidske geometrije. Postoji opšti algoritam za sve planimetrijske zadatke sa dokazivanjem da je neki ugao jednak nečemu. [ jans @ 11.04.2025. 22:13 ] @
Citat: Nedeljko: Postoji opšti algoritam za sve planimetrijske zadatke sa dokazivanjem da je neki ugao jednak nečemu. Gde mogu pronaći navedeni algoritam? [ Nedeljko @ 12.04.2025. 00:47 ] @
Taj algoritam nije za ljude, nego za mašine.
Hint: Polinom deobe kruga 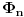 na na  delova je nesvodljiv nad delova je nesvodljiv nad  . Preko njega se lako nalazi minimalni polinom za . Preko njega se lako nalazi minimalni polinom za 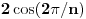 . .Naime, za 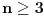 je stepen polinoma je stepen polinoma 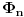 paran broj paran broj 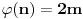 . Lako se nalazi polinom . Lako se nalazi polinom 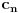 takav da je takav da je 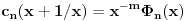 . .Za 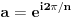 važi važi 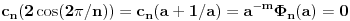 . Polinom . Polinom 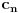 je polinom sa racionalnim (čak celim) koeficijentima stepena je polinom sa racionalnim (čak celim) koeficijentima stepena  . Dokažimo da je nesvodljiv nad . Dokažimo da je nesvodljiv nad  . .U suprotnom bi stepen broja 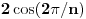 nad poljem racionalnih brojeva bio nad poljem racionalnih brojeva bio 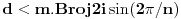 je koren polinoma je koren polinoma 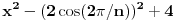 , pa je nad poljem , pa je nad poljem 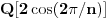 stepena najviše stepena najviše  , pa polje , pa polje 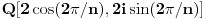 koje sadrži koje sadrži  predstavlja raširenje polja racionalnih brojeva stepena ne većeg od predstavlja raširenje polja racionalnih brojeva stepena ne većeg od 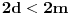 , što je nemoguće jer je zbog nesvodljivosti polinoma , što je nemoguće jer je zbog nesvodljivosti polinoma 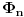 nad poljem racionalnih brojeva stepen broja nad poljem racionalnih brojeva stepen broja  nad poljem racionalnih brojeva jednak nad poljem racionalnih brojeva jednak 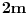 . .To nam omogućava računanje u polju 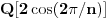 . Pod tim podrazumevam operacije u polju nad brojevima izraženim u vidu linearnih kombinacija sa racionalnim stepenima brojeva . Pod tim podrazumevam operacije u polju nad brojevima izraženim u vidu linearnih kombinacija sa racionalnim stepenima brojeva 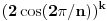 za za 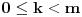 . Zbir, razliku, proizvod i količnik brojeva u toj reprezentaciji možemo izračunati u istoj toj reprezentaciji. Zbog nesvodjivosti polinoma . Zbir, razliku, proizvod i količnik brojeva u toj reprezentaciji možemo izračunati u istoj toj reprezentaciji. Zbog nesvodjivosti polinoma 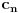 , nula se može predstaviti na tačno jedan način, pa je na taj način dokaziv svaki tačan identitet u tom polju. , nula se može predstaviti na tačno jedan način, pa je na taj način dokaziv svaki tačan identitet u tom polju.Ako su svi uglovi na slici racionalni umnošci punog kruga, možemo izabrati  tako da ugao tako da ugao 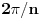 bude najveći zajednički delilac uglova sa slike i pravog ugla. Tada je bude najveći zajednički delilac uglova sa slike i pravog ugla. Tada je 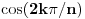 izrazivo kao polinom (sa racionalnim, pa i celim koeficijentima) po izrazivo kao polinom (sa racionalnim, pa i celim koeficijentima) po 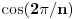 . Takođe je . Takođe je 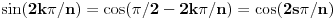 za neko za neko 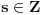 . .Onda račinamo koordinate tačaka sa slike u tom polju. Ako kraci nekog ugla imaju koeficijente pravaca  i i  , gde je , gde je 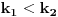 , onda je prema formuli za razliku tangensa tangens tog ugla jednak , onda je prema formuli za razliku tangensa tangens tog ugla jednak 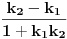 . .[ miki069 @ 12.04.2025. 13:44 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|