nastavak


https://drive.google.com/file/...z4QI7g6TfuhMKpnOeS_ze2ZNI/view

https://drive.google.com/file/...Xbu4eY2IDZQzh/view?usp=sharing

[size=150]sabiranje ili spajanje , kako se izvodi

R a+b=c isto kao i sada , kombinovani brojevi 222+33=2253 , kada budu isti dužni (prazni) spajaju se , ovde 2 i 3 , dobija se 5

R² ovde postoji funkcija operacije ( isto važi za ostale Rⁿ) , 1(R 3+₁4=(3,4₂) , 2(R,R₂) 3+₂4={7 ,(3,4₂)} , 3(R-R₂)3+₃4= {(7, 4₂)},4(R,R₂,R-R₂) , 3+₄4={7,(3,4₂) , (7.4₂)}
(2,3₂+(3,3₂)=(5 ,6₂)

R³ 5(R,R₂ , R₃) , 3+₅4={7 , (3 ,4₂ ), (3 , 0 , 4₃)} , 6(R-R₂, R₃) , 3+₆4={( 7 , 4₂) , ( 3 , 0 , 4₃} , 7(R, R₂-R₃) , .... tako dalje[/size]

Tamo se kao iskaz teoreme navodi nešto što nije tvrdnja.

sabiranje preko članova kombinovanih brojeva

R 22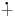332={ 734 , 2372}
postupak 2+3=5 , 2+3=23 , 2+2=4 , spoji se dobija se 734
postupak 2+3=23 , 2+3=5 , 2+2=22 , spoji se dobija 2372
obrnuto
332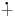22={ 82 ,325 , 62 }
postupak 3+2=5 , 3+2=32 , spoji se dobija se 82
postupak 3+2=32 , 3+2=5 , spoji se dobija se 325
postupak 2+2=4 , 2+2=22 , spoji se dobija se 62

Rⁿ možete sami da razumete iz predhonog oblika sabiranje i gornjeg priloga

Pogledao sam tekst i ne shvatam sta je tu cilj teme. Predlazes novi metricki prostor? Novu algebarsku strukturu, poput prstena, polja, grupe? Neku novu geometriju, koja se kosi sa Euklidom, Lobacevskim, Hilbertom?

Takodje, kao sto kaze Nedeljko:

* Aksioma je prostoprosirena recenica kojom se nesto definise jasno, koncizno i precizno i koja se ne dokazuje.
* Teorema se dokazuje, ali njena formulacija mora isto tako da bude u vidu tvrdnje poput - voda nema ni ukus ni miris.

B3R1
što se tiče (Euklidom, Lobacevskim, Hilbertom) delimično tačno , evo zašto sam postavio ovaj post
https://drive.google.com/file/...Z_scf_837bxqz/view?usp=sharing
dokaz da ne postoji realni i iracionalni brojevi
https://drive.google.com/file/...TAmmPCD110Jha/view?usp=sharing
ako koristimo postojeće brojeve , ne možemo opisati brojevima
1.11
2.11
3.32132

proučavajući sadašnji matematiku došao sam do zaključka da je sve geometrija , onda sam smislio da postoji matematički prostor , i da postoji samo jedak aksiom , sve ostalo potiče iz aksioma i predhodnih dokaza .

pošto vidim da neke stvari ne razumete
aksiom
postoji ( beskonačno osnove ) koja potiče :
0-1( 0-1, polazna osnova
0-0.1 ( 0 - 0.'-1 koja je deset puta manja od polazne osnove
0- 0.01 ('-0.0.01 koja sto puta manja od polazne osnove
...


teorema 1

https://drive.google.com/file/...SoOiwij0_R3Xc/view?usp=sharing

na slici je prikazano za dužine , isto je za praznine ( ne postoji duž) , i za sve ostale vrednosti iz aksioma

dobijamo polupravu , dobijamo praznu polupravu

ako želite mogu svaku teoremu da objasnim ovako

restart

predhodno izlaganje ima greške




izgleda da vam mnogo nejasno

aksim
https://drive.google.com/file/...Jkw6mSV4_s4te/view?usp=sharing

Osnovna dužina
1.polazna osnova 0-1
2 deset puta manja od polazne osnove 0-0-1
3.sto puta manja od polazne osnove 0-0.01
,,,
beskonačno

Osnovna praznina
1. polazna osnova 0-1
2 deset puta manja od polazne osnove 0-0.1
3.sto puta manja od polazne osnove 0-0.01
,,,
beskonačno
Teorema 1
https://drive.google.com/file/...6SNZYbUxPvS-s/view?usp=sharing

vršimo spajanje 1 ( 2 , 3 , ... , beskonačno )
dobijamo
polupravu
prazna poluprava
duž
praznina

teorema 2
dajemo ime tačkama spajanje (0 , 1 , 2, 3 , ...) ( 0 , 1 , 2 , 3 , ...) , ostale tačke se podrazumevaju i prestavljene su simbolom za beskonačno , uporenje sa sadašnju matematiku u skup realnih broja , između dva cela broja postoji beskonačno brojeva
https://drive.google.com/file/...a6bCM94YOw7xW/view?usp=sharing

Definisanje osnovnog skup i skupa

teoreme 3 , 4 , 5 su zadužene za sve realne brojeve , mislim da vam je to jasno
teoreme 6 ,7 postoje kombinovane poluprave ( postoji beskonačno oblika ) i kombinovane duži

Kad ćeš da uvedeš neku relaciju poredka?
Množenje?

Matematika se zasniva na potpuno uređenom Polju.
Ti to još uvek nemaš.

A ti stvarno nešto očekuješ.

Ovaj član foruma već 15 godina kači po forumima isto ovo sr* bez ikakve izmene. Nema tu ničega.

Čak i da tu nema ničega, to nije razlog da nečiji rad nazoveš sr* ...

Milija, Majore,

znaš kako je to,

- kada na Forumu Elektronike vidim da neko *Palahhmmuudiii za SVE pare,
a se pri tom ne miče/pomera se od Početnog Stava i razmišljanja,

i ja bi tada najradije napisao:

- Hallo Požega, ne sehhhrrriii Više!
---------

Mislim "u Afektu" trenutno svašta može čovek da napiše,

a
- sve zbog nečijeg upornog "Gužvanja Teme" i "Igre na sred Terena Bez Lopte".

Eto ti Majore objašnjenje za Djokin Txt.

ENDE

pOz

PS: 😉
https://vukajlija.com/u-afektu/78027

Roberte, jel proradio HP 5L?

https://www.geogebra.org/search/werto

geo gebra , dokaz kako se dobija ravan kao dokaz

pomeranjem tačke F seće prostor , tačka C menja se ugao između pravih

Najradije bi napisao, ali ne napišeš jer si pristojna osoba, ne može da "gužva temu" kad je njegova tema tj. koju je on otvorio. Kad već pričamo o svemu tvoj post je off topic zar ne?

da vidimo koliko ste naučili

342+₂72 , 56123+₃34

342₂72 , 56123₃34

novogodišnji poklon

https://drive.google.com/file/...frWVPDS5__Jvt/view?usp=sharing

Biće da ti nešto ne razumeš, uvodiš neke oznake koje veze nemaju sa usvojenim oznakama u matematici, izmišljaš neku matematiku koja ne postoji, pričaš o tome da "ne postoje realni brojevi", i da ne navodim dalje.
Nisi ni prvi, niti poslednji, koji izmišlja nešto misleći da je originalno i revolucionarno.

Koliko ima onih koji objavljuju "dokaze" za trisekciju ugla ili kvadraturu kruga, "dokaz" Godlbahove hipteze i sl.

Ne traći vreme na gluposti, pozabavi se recimo Rimanovom hipotezom, ako je dokažeš, nagrada je milion dolara ;)

Ovo me podseća na ono kad su slepom čoveku dali turpiju za drvo tz. rašpa, a on kaže "veću glupost u životu ne pročitah".

počnimo od prepostavke da sam ja glup za matematiku , onda ti meni objasni matematički
ima n(n veće od 4) vektora , svi jednakog intiziteta međusobno su spojeni jednakim uglovima ( raztličitih od 180 stepeni ) , koja bi bile to operacije , odnosno suprotna operacije , ne geometriski već računskim putem , precizno odrediš pravac i smer( ne .gore.dole.levo .desno) rešenja

Uveo si pretpostavku da si glup za matematiku. Pod tom pretpostavkom ti se matematika ne može objasniti.

Jel to teorema ili aksioma?

Definicija glupog za matematiku je neo kome se matematika ne može objasniti.

To je vrlo bitno za razne stručnjake koji u javnosti nešto tvrde.
Bilo bi bitno znati koliki ima IQ stručnjak koji barata nekim znanjem.
Ako nije dovoljno veliki IQ to onda nije pravi stručnjak.

Trebalo bi da bude obavezan test inteligencije za sve javne funkcije.

Mnogo filozofirate , a nemate rešenje koje sam vam postavio ,

bla bla ...

Vektori spojeni uglovima?

Prvo nauči neke osnove, pa terminologiju, pa, ako baš hoćeš da se baviš nekim vektorima, imaš neke vektore kod Lattice-Based Cryptography, ako baš voliš da se baviš matematikom i smatraš da možeš da doprineseš nekim novim otkrićima, to je jedna od aktuelnih tema. Pa još ako pronađeš neki bolji i brži algoritam za enkripciju, možeš i da ga patentiraš ;)

ove i slikovnica onima koji ne razumeju tekst

/www.geogebra.org/calculator/tzjsfr3a

uglovi izmeću vektore BCD ,CDE , DEF , EFG

Imam Ja rešenje al' imam veliki bol u preponama te stim prvenstveno mislim na svoje zdravlje!

biljanica,

Koliko imaš godina. Mislim, ako si zakasnio za Filcovu medalju, da vidimo za Abelovu nagradu.

roden

2.5.1967 , pa izraćunaj

Dečkić.............

Ne, počećemo od pretpostavke da sam ja najgluplji za matematiku. Objasni ti meni matematički sledeće.

Čitam ja tako uvodno poglavlje Lajbnicov univerzum i dođem do ovoga:



a onda mi prokuva mozak.

A što od njega tražiš obješnjenje?

0.000...001 gde je ...(beskonačno nula)
pa je ova nestandarna analiza čista glupost

Nestandardna analiza ima istu snagu kao standardna (preko epsilon-delta računa). Postoji princip prenosa kojim se svako standardno rešenej transformiše u nestandardno i obrnuto.

Standardna analiza nema beskonačno male, niti beskonačno velike veličine jer su sa epsilon-delta računom nepotrebne. Zasniva se na polju realnih brojeva koje nema beskonačno male i beskonačno velike veličine.

Polje realnih brojeva se uvodi aksiomatski. Postoje aksiome uređenog polja i aksiome neprekidnosti. Zajedno imaju tačno jedan model do na izomorfizam i to je polje realnih brojeva.

Aksiome neprekidnosti imaju razne ekvivalentne formulacije.

Arhimedova aksioma (prestiživosti) uz aksiome uređenog polja je ekvivalentna tome da se to polje može utopiti u R. Pritom, se proizvoljno uređeno polje može utopiti u R na najviše jedan način. Dakle, uz arhimeda može na tačno jedan način. Do na izomorfizam, arhimedovska polja su tačno potpolja od R. Ipak, ovde je značajnije drugo tumačenje te aksiome. Ona je ekvivalentna nepostojanju beskonačno malih veličina.

Kada Arhimedovoj aksiomi dodamo Kantorovu aksiomu (o umetnutim odsečcima) daje punu aksiomatizaciju polja realnih brojeva.

Dakle, negacija Arhimedove aksiome je ekvivalentna tome da sledeći beskonačan niz formula ima rešenje:

.

Priemtimo da u polju realnih brojeva svaki konačan podskup navedenog skupa formula ima rešenje, ali da ceo beskonačan skup navedenih formula nema rešenje.

Svaka aksioma je nekakav alat. U nestandadnoj analizi smo se odrekli Arhimedove aksiome, pa nam treba nekakva kompenzacija u vidu nekog principa koji ne možemo imati zajedno sa Arhimedovom aksiomom jer ako ih možemo imati zajedno, koristićemo ih zajedno, to jest ne bismo se odricali Arhimedove aksiome zbog nečega što možemo imati zajedno sa njom.

Kompenzaciju imamo u principu prebrojive zasićenosti. Za ma koji konačan niz promenljivih i ma koji beskonačan niz uslova po njima važi sledeće:

Ako svaki konačno mnogo od tih uslova ima rešenje, onda ceo niz uslova ima rešenje.

Pritom se skup uslovs mora ograničiti. Na početku imamo sledeće:

Izraze formiramo od operacijskih znakova (na početku za sabiranje i množenje), promenljivih i konstanti (na početku realnih). Na početku su to samo polinomi.

Osnovni uslovi su da je neki izraz veći od nule ili da je veći ili jednak ili jednak. Svi se mogu izraziti preko veće ili preko veće ili jednako.

Uslovi se mogu bulovski kombinovati (i ili ne).

Uslovi se mogu kvantifikovati kvantorima "za svaki" i "postoji" koji se odnose na veličine (sve i konačne i beskonačno velike i male), ali ne na operacije i relacije.

Dakle, možemo napisati "za svako x postoji y tako da važi U(x,y,z)", gde je U neki uslov i to će na kraju biti uslov po z.

Možemo i prenosit operacije i relacije iz standardne analize u nestandardnu. Recimo, sinus je jedna unarna operacija, dok je "m je ceo broj manji od celog broja n" binarna relacija. Prilikom prenošenja, prenosimo sve uslove koji važe za njih i tako proširujemo jezik primenjujući princip prebrojive zasićenosti i princip daljeg proširivanja jezika i na dobijjeno proširenje.

Sinus se u nestandardnoj analizi odnosi i na beskonačno male i velike veličine, a po zakonitostima prenosa i prebrojive zasićenosti.

A bre Nedeljhko napisi upozorenje - nije za decu preko 12 godina ... Ovo stivo je opasno !!!

Biljanica, ako imaš malo vremena, mogao bi da mi rešiš jedan zadatak.

Za koje važi ?

ako je r jednak n ( celi brojevi osim nule)

Zanimljivo, danas sam naučio nešto novo.

Koren iz dva je racionalan broj.

Osim 1 i (-1) koji su trivijalna rešenja, kako bi dokazali da nema drugih rešenja?
Ili ih ima?

1/n su takođe rešenja.
Pitanje je da li bilo koji racionalni broj koji nema 1 u brojiocu može da proizvede racionalni broj, odnosno da li

može da bude racionalni broj kada se primeni p-ti koren

U pravu si.

Nema drugih rešenja osim 1/n i -1/n. Prvo uraditi za pozitivne i koristiti uzajamnu prostost od p i q.

Neka su prirodni brojevi takvi da važi , i pri čemu su napisani razlomci neskratljivi. Dakle,

(1) ,

odnosno i . Pošto su i uzajamno prosti, oni nemaju nijedan zajednički prost delilac, pa ga nemaju ni i , pa su i oni uzajamno prosti, pa i , odnosno za neke prirodne brojeve važi

(2) i .

Odatle i iz (1) sledi da je , odnosno . Odatle i iz (2) sledi da pošto su i uzajamno prosti, mora biti , odnosno

i .

Ako za prirodan broj i prost broj sa označimo najveći ceo broj takav da , onda iz prethodnog sledi da za ma koji psost broj važi i , pa pošto su i uzajamno prosti, važi i , pa pošto to važi za svaki prost broj brojevi i su potpuni -ti stepeni, odnosno za neke pridodne brojeve i važi i . Pritom je moguće samo za .

Dakle, jedini pozitivni racionalni brojevi za koje je racionalan broj su recipročne vrednosti pridodnih brojeva.

Pronađimo negativne. Neka su i prirodni brojevi za koje je racionalan broj. Da bi to bilo definisano, potrebno je i dovoljno da bude neparno. Tada važi da je broj



racionalan broj, što znači da je racionalan broj, pa prema prethodnom mora biti , pa su jedini negativni racionalni brojevi za koje je racionalan broj oblika gde je prirodan broj.