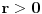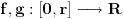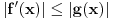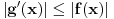[ Nedeljko @ 03.03.2025. 02:16 ] @
|
[ miki069 @ 03.03.2025. 19:19 ] @
Jel ideja primena Rolove, Lagranžove ili Košijeve teoreme?
Ili nešta četvrto? [ Nedeljko @ 03.03.2025. 22:15 ] @
Kako god uspeš. Ja nisam našao rešenje u potezu, odnosno primenom jedne stvari.
[ miki069 @ 05.03.2025. 16:43 ] @
Za sada najmanje r je pi/2.
Funkcije su: f(x)=cos(x) i g(x)=sin(x). Ko nudi manje r? [ Nedeljko @ 05.03.2025. 17:31 ] @
Mogao si te funkcije da pomnožiš i nekom pozitivnom konstantom ili da funkciji g promeniš znak.
To je minimum, ali kako dokazati? Minimum se dostiže samo za takve funkcije, gde je f jednako kosinusu pomnoženim nekom pozitivnom konstantom, a g jednako sinusu pomnoženim istom tom konstantom i još eventualno sa (-1). [ Nedeljko @ 05.03.2025. 17:52 ] @
Evo izvora:
Rešenje prvog zadatka je nepotrebno zakomplikovala. [ miki069 @ 05.03.2025. 19:04 ] @
[ Nedeljko @ 05.03.2025. 19:14 ] @
Ispunjavaju. Funkcija ne mora biti surjektivna,
[ mjanjic @ 06.03.2025. 17:27 ] @
Nije fazon nalaziti rešene primere, pa postavljati ovde, podseća me na voditeljke/voditelje u kvizovima, kad se prave pametni čitajući odgovore na pitanja na koja niko od tamičara nije dao tačan odgovor, pa ispadaju ne znam koliko pametniji od tih takmičara.
Sa druge strane, naš obrazovni sistem je malo.... Sećam se zadatka sa nekom zapadnog univerziteta, SAD ili Kanada, gde se već u prvom semestru uči gama funkcija, ali samo osnovne osobine, potom odmah diferencijalne jednačine, opet najosnovnije, pa se kasnije uče neke teže stvari u narednim semestrima. Sećam se zadatka sa jednog takvog kursa: Ne znajući za postojanje trigonometrijskih funkcija, diskutovati rešenja diferencijalne jednačine y'' + y = 0. Da li bi taj "zadačić" znali da reše čak i oni koji kod nas diplomiraju matematiku je neko drugo pitanje, nije do sposobnosti i znanja, već se ovde i dalje forsira "ruska škola", koja ima potpuno drugačiji pristup, koji je možda dobar za one naj-naj-najbolje, ali nije dobar za one koji su malo ispod njih, o prosečnima da ne govorimo, a tek o primeni u privredi bolje ne pričati. Sećam se i zadatka tipa "naći bar jednu funkciju f(x) koja je nenegativna na intervalu [0, +∞), nema limes u +∞, a njen određen integral na tom intervalu ima konačnu vrednost" (što će reći da je površina između grafika te funkcije i x-ose konačna). Sreća da sam nekako "slučajno" povezao jedan primer iz telekomunikacija sa nekim primerom reda iz matematike čija je vrednost (π^2)/6, pa konstruisao jednu takvu funkciju :) Donekle forsiranje učenja napamet i rešavanja tipskih zadataka koji na prvi pogled nigde nemaju primenu je jedan od krivaca zašto naši diplomci imaju kasnije problem sa "out of the box" razmišljanjem, inoviranjem rešenja, itd. [ Nedeljko @ 06.03.2025. 18:44 ] @
Ja sam ovde postavio zadatke sa onog videa koji nisu tamo rešeni.
Naravno da znam na šta se zadatak y''+y=0. Ko to ne zna, taj ne zna kako funkcioniše matematika. [ miki069 @ 07.03.2025. 06:49 ] @
Mjanic:
Kakve veze ima Gama funkcija sa diferencijalnim jednačinama? Laplasova transformacija ima. Super im je plan i program ako prvo rade gama funkciju. [ Nedeljko @ 07.03.2025. 09:27 ] @
Citat: mjanjic: Nije fazon nalaziti rešene primere, pa postavljati ovde, podseća me na voditeljke/voditelje u kvizovima, kad se prave pametni čitajući odgovore na pitanja na koja niko od tamičara nije dao tačan odgovor, pa ispadaju ne znam koliko pametniji od tih takmičara. Ja to nisam ni radio. U klipu se prikazuje test sa 12 zadataka - A1-A6 i B1-B6, od čega su tamo rešeni A1 i A6. Ja sam ovde postavio zadatke A3 i A4, koje sam samostalno rešio. Recimo, zadatak A2 je lagan. [ mjanjic @ 07.03.2025. 11:15 ] @
Izvinjavam se, mislio sam da su svi rešeni.
Rešenja obično mogu biti relativno lagana, ali postoji i "ruski" pristup koji sam video u nekim njihovim knjigama, ono što se inače dokazuje na pola stranice, oni dokazuju na bar 3-4 strane, kao neki stroži dokaz na drugačiji način... sećam se tako dokaza formule za inverznu matricu, može i na trećinu stranice, a može i na 5 stranica. miki069, nema veze Gama funkcija sa diferencijalnim, radi se o dva različita zadatka. A to da li ima smisla takve stvari raditi već u prvom semestru je neka druga priča, to je kurs na Computer Science za najbolje studente, nije za boraniju. Ne gleda se šta si naučio samo u prvom ili trećem semestru, nego šta si naučio do kraja studija i da li si razvio sposobnosti da rešavaš nove probleme koje do tog trenutka nisi video. Ali, verovatno mi sve znamo bolje. [ Nedeljko @ 07.03.2025. 11:32 ] @
Nama je u jesen 1993 na prvom semstru studija prof. Dragoljub Aranđelović na petom času radio kategorije i funktore iz Matematičke analize 1.
[ miki069 @ 07.03.2025. 12:36 ] @
Gledao sam predavanja iz Matematike sa prestižnog Berklija. Dosta gluposti sam video. Profa 3 sata objašnjava definiciju linearne zavisnosti vektora.
To kod nas ide za pola sata. Najverovatnije zato što su naši studenti inteligentniji od američkih. Daj link do predavanja na tom kursu na Computer Science. Možda su bolji od Berklija. [Ovu poruku je menjao miki069 dana 07.03.2025. u 14:03 GMT+1] [ mjanjic @ 07.03.2025. 14:44 ] @
To već nemam, bio je u pitanju Toronto, tamo pre 20 i neku godinu, u pitanju su bili domaći zadaci, neki kolega pomagao svojo rođaci da to uradi.
Predavanja su svugde uglavnom takva, pogledaj izvikani CS50, onaj David Malan je prošle godine imao platu 1.7 miliona (oko 395k je osnovna plata, ostalo projekti i ko zna šta još), a kad pogledaš predavanja, on kao da se zeza. Ali su zato vežbe, domaći zadaci i projekat ubijanje, a vežbe drže studenti master studija i doktoranti koji već rade u velikim kompanijama. Nego, kad je već matematika... YT kanal Oxford Mathematics ima zanimljivih videa, mislim sa tačke gledišta koliko pišu po onim "tablama", tu i tamo je poneki širok kadar sa udaljenije kamere, gde se vidi koliko ima onih fleksibilnih rolo-tabli... https://www.youtube.com/watch?v=Bjnj8-HMjIA Kod svih tih predavanja mi je zanimljivo da mnogi koriste papire/podsetnike, kod nas je uvek halabuka na takve profesore, jer studente propituju "u sitna crevca", dok oni na predavanjima čitaju i prepisuju sa tih papira, kad ono slična priča i tamo na tim elitnim univerzitetima. Kad si pomenuo Berkli, zanimljivo je da oni daju mogućnost nastavnicima da napreduju u zvanju čak i ako se ne bave naukom, tj. mogu bez nekih jakih naučnih referenci stići do zvanja redovnog profesora, a na osnovu toga što su se istakli u nastavi, čak u nekom dokumentarcu se tvrdi da su po tome jedinstveni. [ Nedeljko @ 07.03.2025. 16:43 ] @
Nego, da li nekoga zanima zadatak, ideje, rešenje. Kucati ili ne kucati (rešenje)? Naravno da nisam postavio zadatak pre nego što sam ga rešio.
[ MajorFatal @ 07.03.2025. 17:32 ] @
Zanima ...
[ miki069 @ 07.03.2025. 19:25 ] @
Zanima...
[ miki069 @ 07.03.2025. 19:32 ] @
Mene još više zanima diferencijalna jednačina:
y'' + y = 0 Ako se traži rešenje, a kao ne znamo da je to y = cos(x) + sin(x), jedini način je preko polinoma beskonačnog stepena. Posle se ispostavi da su ti polinomi Mekloranovi razvoji za te dve funkcije. Ne verujem da student I godine bilo kog fakulteta ima predzanje o redovima i to funkcionalnim alternativnim redovima. Mjanic spominje diskusiju rešenja? Ako je tražena geometrijska interpretacija rešenja, za njih je preteška i interpretacija rešenja mnogo lakše diferencijalne jednačine: y' + y = 0 Šta je konkretno bio zadatak? Može da se otvori i posebna tema, da ne razvodnjujemo Nedeljkovo remek delo. [Ovu poruku je menjao miki069 dana 07.03.2025. u 20:45 GMT+1] [ Nedeljko @ 07.03.2025. 22:03 ] @
Pretpostavimo da su
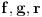 kao u zadatku, pri čemu je kao u zadatku, pri čemu je 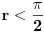 i izvedimo protivrečnost. i izvedimo protivrečnost.Teorema 1: Neka su 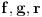 kao u zadatku. Tada je kao u zadatku. Tada je 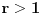 . .Dokaz: Iz neprekidnosti funkcije  na ograničenom zatvorenom intervalu na ograničenom zatvorenom intervalu 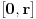 sledi da funkcija sledi da funkcija  na tom intervalu dostiže najveću vrednost na tom intervalu dostiže najveću vrednost  u nekoj tački u nekoj tački  . Iz . Iz 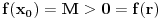 sledi da je sledi da je 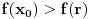 , a samim tim i , a samim tim i 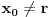 , odnosno , odnosno 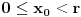 . Za neko . Za neko 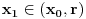 važi sledeće: važi sledeće: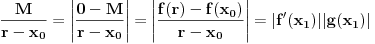 , ,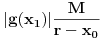 , ,Za neko 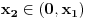 važi sledeće: važi sledeće: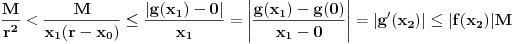 , ,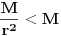 , ,što zajedno sa 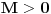 daje daje 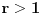 . .Kraj dokaza. Teorema 2: Neka su 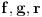 kao u zadatku. Tada postoji kao u zadatku. Tada postoji 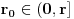 , kao i neprekidne funkcije , kao i neprekidne funkcije 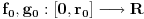 diferencijabilne na intervalu diferencijabilne na intervalu 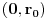 takve da važi takve da važi 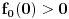 , , 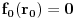 , , 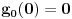 , , 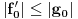 , , 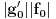 , kao i , kao i 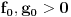 na na 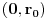 . .Dokaz: Iz neprekidnosti funkcije  na ograničenom, zatvorenom intervalu na ograničenom, zatvorenom intervalu 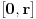 i i 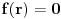 sledi da postoji najmanja nula sledi da postoji najmanja nula 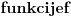 na intervalu na intervalu 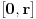 . Pritom, iz . Pritom, iz 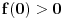 sledi da je sledi da je 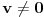 , a samim tim i , a samim tim i 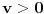 . Dakle, . Dakle,  je različito od nule na intervalu je različito od nule na intervalu 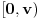 na zbog neprekidnosti na njemu ne menja znak, pa iz na zbog neprekidnosti na njemu ne menja znak, pa iz 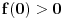 sledi da je sledi da je 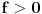 na intervalu na intervalu 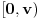 . .Iz Teoreme 1 sledi da je 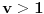 . Dokažimo da funkcija . Dokažimo da funkcija  nema nula na intervalu nema nula na intervalu 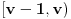 . Dokaz izvodimo svođenjem na protivrečnost. Pretpostavimo da je . Dokaz izvodimo svođenjem na protivrečnost. Pretpostavimo da je 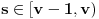 nula funkcije nula funkcije  i izvedimo protivrečnost. Tada bi za funkcije i izvedimo protivrečnost. Tada bi za funkcije 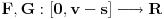 definisane sa definisane sa 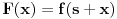 i i 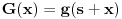 važilo da su neprekidne na važilo da su neprekidne na 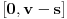 , diferencijabilne na , diferencijabilne na 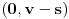 , kao i , kao i 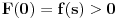 , , 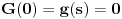 , , 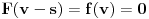 , , 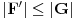 i i 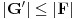 , pa prema Teoremi 1 važi , pa prema Teoremi 1 važi 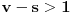 suprotno izboru broja suprotno izboru broja  . .Iz neprekidnosti funkcije  na ograničenom i zatvorenom intervalu na ograničenom i zatvorenom intervalu 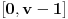 i i 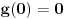 sledi da funkcija sledi da funkcija  ima najveću nulu ima najveću nulu  na intervalu na intervalu 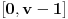 . Pošto funkcija . Pošto funkcija  nema nula na intervalu nema nula na intervalu 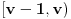 , zaključujemo da je , zaključujemo da je 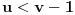 i da je i da je  najveća nula funkcije najveća nula funkcije  na intervalu na intervalu 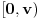 . Dakle, funkcija . Dakle, funkcija  nema nula na intervalu nema nula na intervalu 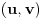 , pa na njemu ne menja znak, pa važi jedno od sledećeg: , pa na njemu ne menja znak, pa važi jedno od sledećeg:a) 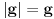 na na 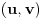 , ,b) 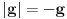 na na 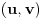 . .Iz neprekidnosti funkcija  , , 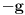 i i 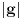 zaključujemo da ista jednakost važi i na intervalu zaključujemo da ista jednakost važi i na intervalu 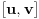 . .Sada se lako zaključuje da su traženi uslovi ispunjeni za 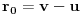 , , 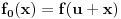 i i 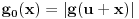 . .Kraj dokaza. Dokažimo napokon da je 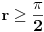 . Pretpostavimo suprotno i izvedimo protivrečnost. Prema Teoremi 2 možemo bez umanjenja opštosti pretpostaviti da je . Pretpostavimo suprotno i izvedimo protivrečnost. Prema Teoremi 2 možemo bez umanjenja opštosti pretpostaviti da je 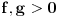 na na 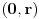 . Definišimo funkciju . Definišimo funkciju 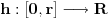 na sledeći način: na sledeći način: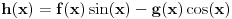 . .Važi sledeće: 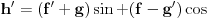 . .Iz 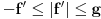 sledi da je sledi da je 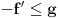 , odnosno , odnosno 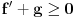 . Iz . Iz 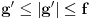 sledi da je sledi da je 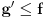 odnosno odnosno 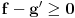 . Odatle i iz . Odatle i iz 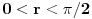 sledi da je sledi da je 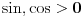 na intervalu na intervalu 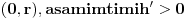 na na 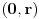 . Odatle i iz neprekidnosti funkcije . Odatle i iz neprekidnosti funkcije 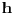 na na 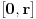 sledi da je funkcija sledi da je funkcija 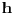 monotono neopadajuća na monotono neopadajuća na 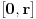 . .Odatle i iz 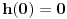 i i 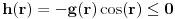 sledi da je funkcija sledi da je funkcija 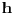 konstantno jednaka nuli, odnosno da je konstantno jednaka nuli, odnosno da je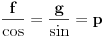 na na 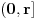 za neku funkciju za neku funkciju  koja je neprekidna na koja je neprekidna na 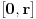 i diferencijabilna i pozitivna na i diferencijabilna i pozitivna na 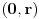 . Drugim rečima, važi . Drugim rečima, važi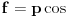 , , 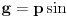 . .Iz 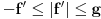 sledi da je sledi da je 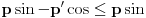 , odnosno , odnosno 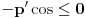 , odnosno , odnosno 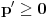 . .Iz 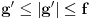 sledi da je sledi da je 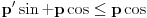 , odnosno , odnosno 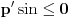 , odnosno , odnosno 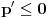 . .Dakle, 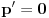 na na 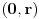 , pa je neprekidna funkcija , pa je neprekidna funkcija  konstantna na konstantna na 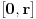 . Pritom je . Pritom je 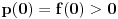 , pa za pozitivnu konstantu , pa za pozitivnu konstantu  važi važi 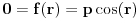 , odnosno , odnosno 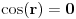 što je u suprotnosti sa pretpostavkom da je što je u suprotnosti sa pretpostavkom da je 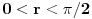 . .[ elektromonter @ 08.03.2025. 09:44 ] @
Citat: miki069 Ne verujem da student I godine bilo kog fakulteta ima predzanje o redovima i to funkcionalnim alternativnim redovima. Ima i to. Na primer PMF 1.Godina Računarske nauke. Rade stepene redove a pre Bolonje je toga bilo i više sa alternativnim i funkcionalnim redovima. [ miki069 @ 08.03.2025. 10:18 ] @
U prilogu koji si dao nema nikakvih stepenih redova.
To se radi u Analizi-3 u drugoj godini. Na PMF u Kragujevcu. [ Nedeljko @ 08.03.2025. 11:54 ] @
Poenta je u vezi između analize i geometrije.
Ako je geometrijski sinus 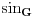 , koji svakom uglu kao geometrijskoj figuri pridružuje realan broj, definisan preko sličnosti trouglova i ako je definisana mera , koji svakom uglu kao geometrijskoj figuri pridružuje realan broj, definisan preko sličnosti trouglova i ako je definisana mera  ugla, koja svakom uglu kao geometrijskoj figuri pridružuje pozitivan realan broj tako da podudarnim uglovima pridružuje isti realan broj i koja uniji dva ugla pridružuje zbir brojeva pridruženih tim uglovima u slučaju kada je presek tih uglova prava, a unija neki veći ugao, onda se dokazuje da je mera ugla jednoznačno određena do na multiplikativnu konstantu. Tada možemo definisati analitički sinus ugla, koja svakom uglu kao geometrijskoj figuri pridružuje pozitivan realan broj tako da podudarnim uglovima pridružuje isti realan broj i koja uniji dva ugla pridružuje zbir brojeva pridruženih tim uglovima u slučaju kada je presek tih uglova prava, a unija neki veći ugao, onda se dokazuje da je mera ugla jednoznačno određena do na multiplikativnu konstantu. Tada možemo definisati analitički sinus 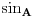 koji svako realnom broju pridružuje realan broj i takva da važi koji svako realnom broju pridružuje realan broj i takva da važi 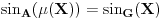 za svaki ugao za svaki ugao  i uz odgovarajuće neprekidno i periodično produženje. Tada se dokazuje da postoji pozitivna konstanta i uz odgovarajuće neprekidno i periodično produženje. Tada se dokazuje da postoji pozitivna konstanta  koja zavisi od izbora mere pravog ugla, takva da važi koja zavisi od izbora mere pravog ugla, takva da važi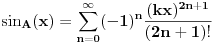 i slično za kosinus, pri čemu ista pozitivna konstanta učestvuje i u formuli za kosinus. Pritom je moguće odabrati meru pravog ugla tako da bude 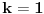 . Tada je moguće koristiti stepene redove za rešavanje tih diferncijalnih jednačina i geometrijsku interpretaciju tih redova jer se zna da to jeste njihova geometrijska interpretacija. . Tada je moguće koristiti stepene redove za rešavanje tih diferncijalnih jednačina i geometrijsku interpretaciju tih redova jer se zna da to jeste njihova geometrijska interpretacija.Naravno, postoje i prečice da se iz definicija funkcija 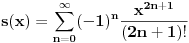 , ,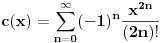 može izvesti da su periodične sa istim periodom na kojim intervalima (izraženim preko perioda) kog znaka, gde su monotono rastuće, a gde monotoo neopadajuće, gde su konveksne, a gde konkavne. Prečica je kraća ako se koriste izvodi, ali je moguće i bez njih, samo sa neprekidnošću. [ mjanjic @ 08.03.2025. 12:45 ] @
U vezi diferencijalne jednačine y'' + y = 0, ako se dobro sećam, tražilo se samo da se diskutuju osobine rešenja, bez znanja o postojanju trigonometrijskih funkcija.
Kako se na osnovu drugog izvoda mogu odrediti prevojne tačke funkcije (tj. grafika funkcije), a za koje važi da je drugi izvod jednak 0, iz gornje diferencijalne jednačine sledi da f(x) ima prevojne tačke u preseku sa x-osom, tj. u tačkama koje su istovremeno i nule te funkcije. Pored toga, vrednosti drugog izvoda funkcije i vrednosti same funkcija imaju istu apsolutnu vrednost i suprotan znak u svim ostalim tačkama, što znači da prvi izvod funkcije (koeficijent pravca tangente na grafik funkcije) opada kada je funkcija pozitivna i raste kada je funkcija negativna, i te vrednosti se menjaju istom "brizinom" počevši od tačke gde je f=0. Znajući ovo, čak se može približno skicirati grafik takve funkcije. Ovo, onako, laički, na osnovu sećanja :) Kako se na istom kursu pominjala i Gama funkcija, ali ne preko integrala, već kao funkcija koja za prirodne brojeve praktično predstavlja n! (faktorijel) i kako su tu pominjane osobine, između kojih i logaritamska konveksnost, ne znam da li su nešto od tih činjenica mogli da primene i na diskusiju o osobinama rešenja gornje diferencijalne jednačine. [ elektromonter @ 08.03.2025. 16:29 ] @
Evo ispravan link na obavezan ispit Matematička analiza 1. Ispit je na 1. godini studijskog programa Računarske nauke.
 [ Nedeljko @ 08.03.2025. 16:30 ] @
Osloniću se na teoriju linearnih diferencijalnih jednačina i neprekidnost i diferencijabilnost funkcija i osobine izvoda kao predznanje.
Iz teorije homogenih linearnih diferencijalnih jednačina se zna da postoje tačno dva rešenja do na linearnu nezavisnost. Obeležimo ih sa  i i  uz odgovarajuće početne uslove uz odgovarajuće početne uslove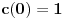 , , 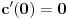 , , 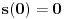 , , 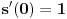 . .Za funkciju 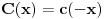 se ispostavlja da zadovoljava isti Košijev zadatak kao funkcija se ispostavlja da zadovoljava isti Košijev zadatak kao funkcija  , pa je to ista funkcija, odnosno funkcija , pa je to ista funkcija, odnosno funkcija  je parna. Slično tome, funkcija je parna. Slično tome, funkcija 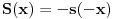 zadovoljava isti Košijev zadatak kao funkcija zadovoljava isti Košijev zadatak kao funkcija  , odakle sledi da je funkcija , odakle sledi da je funkcija  neparna. Dakle, dovoljno ih je proučiti desno od nule. neparna. Dakle, dovoljno ih je proučiti desno od nule.Iz dvostruke diferencijabilnosti funkcije  i iz i iz 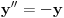 sledi da je sledi da je  četiri puta diferencijabilna funkcija. Takođe, četiri puta diferencijabilna funkcija. Takođe, 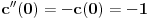 , odakle sledi da funkcija , odakle sledi da funkcija 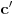 zadovoljava isti Košijev zadatak kao zadovoljava isti Košijev zadatak kao 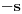 , pa je , pa je 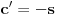 . Na sličan način se zaključuje da je . Na sličan način se zaključuje da je 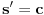 . Iz . Iz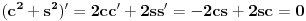 zaključujemo da je funkcija zaključujemo da je funkcija 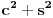 konstantna, pa pošto je u nuli jednaka jedinici, važi konstantna, pa pošto je u nuli jednaka jedinici, važi 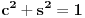 , odakle sledi da su funkcije , odakle sledi da su funkcije  i i  ograničene i da imaju vrednosti u intervalu ograničene i da imaju vrednosti u intervalu 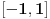 . .Iz 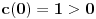 sledi da je funkcija sledi da je funkcija  pozitivna u nekoj okolini nule, pa pošto zadovoljava datu diferencijalnu jednačinu, drugi izvod joj je negativan u istoj toj okolini, pa je prvi izvod opadajuća funkcija u istoj okolini. Iz pozitivna u nekoj okolini nule, pa pošto zadovoljava datu diferencijalnu jednačinu, drugi izvod joj je negativan u istoj toj okolini, pa je prvi izvod opadajuća funkcija u istoj okolini. Iz 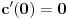 sledi da je sledi da je 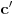 pozitivno u nekoj levoj poluokolini nule, a u desnoj negativno. Dakle, ako funkcija pozitivno u nekoj levoj poluokolini nule, a u desnoj negativno. Dakle, ako funkcija  nema nijednu nulu, onda je stalno poyitivna, izvod joj je desno od nule negativan i sve manji. Na prime, desno od jedinice će stalno biti manji od nema nijednu nulu, onda je stalno poyitivna, izvod joj je desno od nule negativan i sve manji. Na prime, desno od jedinice će stalno biti manji od 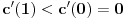 , odakle sledi da će ipak morati negde da preseče x-osu. Međutim, zbog neprekidnosti mora postojati najmanja nenegativna nula , odakle sledi da će ipak morati negde da preseče x-osu. Međutim, zbog neprekidnosti mora postojati najmanja nenegativna nula  funkcije funkcije  . Iz . Iz 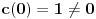 sledi da je sledi da je  . .Dakle, funkcija  je pozitivna na intervalu je pozitivna na intervalu 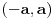 , pa na njemu ima negativan drugi izvod. odatle i iz neprekidnosti sledi da je funkcija , pa na njemu ima negativan drugi izvod. odatle i iz neprekidnosti sledi da je funkcija  konkavna na intervalu konkavna na intervalu 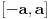 . Ona na intervalu . Ona na intervalu 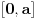 monotono opada. monotono opada.Odatle sledi da je funkcija  na intervalu na intervalu 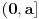 nenegativna i manja od jedinice, pa zbog nenegativna i manja od jedinice, pa zbog 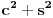 funkcija funkcija  nema nula na tom intervalu, pa na njemu ne menja ynak. Iz nema nula na tom intervalu, pa na njemu ne menja ynak. Iz 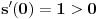 sledi da funkcija sledi da funkcija  raste u nekoj desnoj poluokolini nule, pa je zbog raste u nekoj desnoj poluokolini nule, pa je zbog 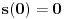 pozitivna u nekoj desnoj šupljoj poluokolini nule. Prema tome, funkcija pozitivna u nekoj desnoj šupljoj poluokolini nule. Prema tome, funkcija  je nenegativna na intervalu je nenegativna na intervalu 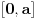 , pa na njemu važi , pa na njemu važi 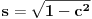 . .Odatle sledi da je 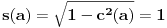 i i 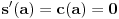 , a onda i , a onda i 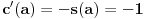 , pa funkcija , pa funkcija 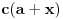 zadovoljava isti Košijev zadatak kao funkcija zadovoljava isti Košijev zadatak kao funkcija 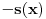 , dok funkcija , dok funkcija 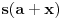 zadovoljava isti Košijev zadatak kao funkcija zadovoljava isti Košijev zadatak kao funkcija 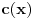 . Dakle, . Dakle, 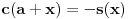 i i 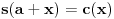 , gde su , gde su  i i  proizvoljne konstante. proizvoljne konstante.Odatle sledi da je 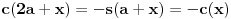 i i 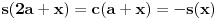 , a odatle i , a odatle i 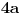 -periodičnost funkcija -periodičnost funkcija  i i  , a samim tim i svih rešenja date diferencijalne jednačine kao linearnih kombinacija , a samim tim i svih rešenja date diferencijalne jednačine kao linearnih kombinacija 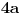 -periodičnih funkcija -periodičnih funkcija  i i  . .Iz 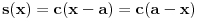 (parnost) sledi da je funkcija (parnost) sledi da je funkcija  na intervalu na intervalu 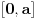 rastuća i konkavna. Odatle i iz rastuća i konkavna. Odatle i iz 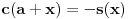 i i 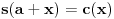 se lako iyvodi gde su funkcije se lako iyvodi gde su funkcije  is is  rastuće/opadajuće, odnosno konveksne/konkavne. rastuće/opadajuće, odnosno konveksne/konkavne.Neka je 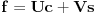 bilo koje rešenje date diferencijalne jednačine različito od nule i neka je bilo koje rešenje date diferencijalne jednačine različito od nule i neka je 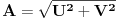 i i 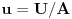 i i 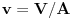 . Tada važi . Tada važi 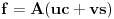 , kao i , kao i 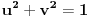 , odakle sledi da je , odakle sledi da je 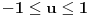 . .Funkcija  na intervaliu na intervaliu 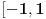 opada od opada od  do do  pa postoji neka tačka pa postoji neka tačka  za koju je za koju je 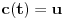 . Tada je . Tada je 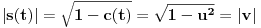 , odnosno , odnosno 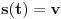 ili ili 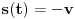 . Neka je . Neka je 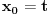 u prvom slučaju, odnosno u prvom slučaju, odnosno 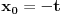 u drugom. u drugom.Iz parnosti/neparnosti sledi da je 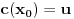 i i 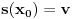 . Dakle, funkcija . Dakle, funkcija  zadovoljava u tački zadovoljava u tački  isti Košijev uslov kao funkcija isti Košijev uslov kao funkcija 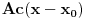 jer važi jer važi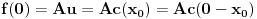 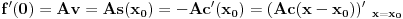 , ,odakle sledi da je 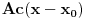 opšte rešenje. opšte rešenje.[ Nedeljko @ 12.03.2025. 20:52 ] @
U videu je rešen prvi zadatak na nepotrbno komplikovan način.
Zanima nas samo vrednost drugog izvoda funkcije 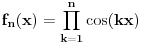 , u tački 0, pri čemu je fukkcija data kao izraz (u ovom slučaju proizvod) po nekim drugim funkcijama, tako da , u tački 0, pri čemu je fukkcija data kao izraz (u ovom slučaju proizvod) po nekim drugim funkcijama, tako da 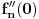 zavisi samo od vrednosti i izvoda tih drugih funkcija do drugog reda u tački 0. zavisi samo od vrednosti i izvoda tih drugih funkcija do drugog reda u tački 0.Ako je 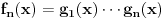 , onda ćemo diferenciranjem tog izraza dva puta dobiti izraz samo po , onda ćemo diferenciranjem tog izraza dva puta dobiti izraz samo po 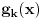 , , 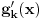 i i 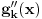 , pa vrednost , pa vrednost 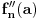 zavisi samo od zavisi samo od 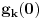 , , 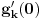 i i 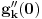 , pa za funkciju , pa za funkciju 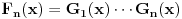 važi važi 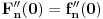 ako je ako je 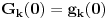 , , 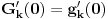 i i 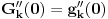 . .Dakle, funkcija 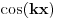 se može zameniti drugom funkcijom koja je u okolini nule aproksimira sa tačnošću do drugog reda, kao što je funkcija se može zameniti drugom funkcijom koja je u okolini nule aproksimira sa tačnošću do drugog reda, kao što je funkcija 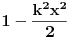 . .Iz istog razloga, prilikom množenja možemo zanemariti članove višeg reda od 2 i tako brzo dolazimo do toga da je 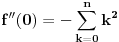 . .Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|