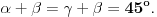Najelegantnije rešenje je preko kompleksne aritmetike. Kada se kompleksni brojevi množe, argumenti im se sabiraju.

Euklid nije znao ni trigonometriju ni kompleksne brojeve.

Ali zanima me rešenje preko kompleksnih brojeva.
Gde se vidi množenje?

Ugao CAB je argument broja 3+i, dok je ugao CEB argument broja 2+i. Pomnoži ta dva broja i dobićeš broj čiji je argument 45 stepeni.

Lepo rešenje.
Dobije se 5+5*i.
Njegov argument je 45 stepeni.

Rešenje pomoću Euklidske geometrije ( VII. razred ).


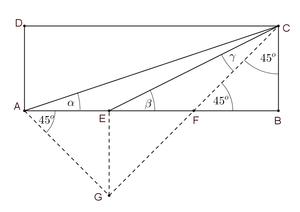
Van datog pravougaonika odredimo tačku G tako da je EG=AE i .
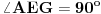
Neka je tačka F središte duži EB, odnosno AE=EF=FB=BC=EG.
Pošto su trouglovi CEB i CAG pravougli, a razmera njihovih kateta je 2:1, ti trouglovi su slični. Sledi da su uglovi naspram dužih kateta podudarni, odnosno
.
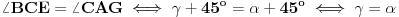
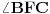
Ugao je spoljašnji ugao trougla FEC, pa je

To je to.