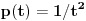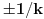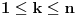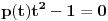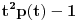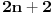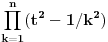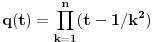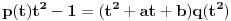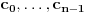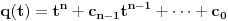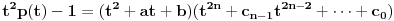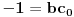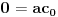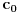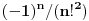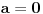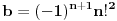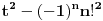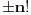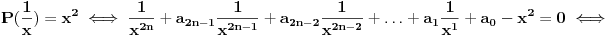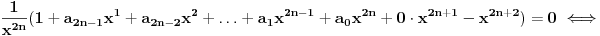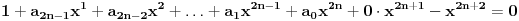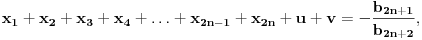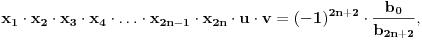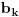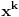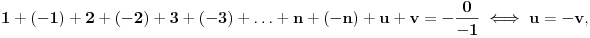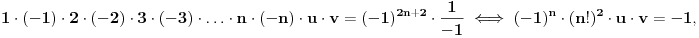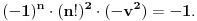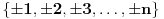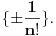[ Nedeljko @ 08.03.2025. 18:49 ] @
| Jedan lagan zadatak sa vida koji sam postavio ovde https://www.elitesecurity.org/p4098333 Napominjem da zadatak tamo nije rešen. Neka je  prirodan broj i prirodan broj i 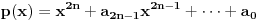 za neke realne za neke realne 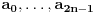 . Ako je . Ako je 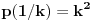 za sve cele brojeve za sve cele brojeve  za koje je za koje je 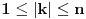 , naći preostala realna rešenja jednačine , naći preostala realna rešenja jednačine 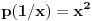 . . |