|
|
[ jans @ 09.05.2025. 00:08 ] @
|
| Napisao sam, u prethodnim temama sa uglovima („Još jedan zadatak sa uglovima“ i „Treći zadatak sa uglovima“ ), da mi nije poznato da li je moguće te zadatke rešiti pomoću Euklidske geometrije. A Miki je u jednoj od poruka napisao:Citat: Nedeljko jasno je da važi stav:
Ako je zadatak rešiv Euklidskom geometrijom sigurno je rešiv i trigonometrijom.
Nisam siguran da važi i obrnuto.
Razlog je i činjenica da „rešavanje zadatka Euklidskom geometrijom“, verovatno različito tumačimo. Zbog toga ću preformulisati pitanje.
Geometrijski zadatak u kojem figurišu uglovi možemo rešavati na dva načina:
1.) U postupku rešavanja koristimo trigonometrijske funkcije;
2.) U postupku rešavanja ne koristimo trigonometrijske funkcije.
Jasno je da svaki zadatak sa uglovima, ako je rešiv, možemo rešiti na 1. način.
Pitanje je da li takav zadatak možemo rešiti na 2. način.
|
[ Nedeljko @ 09.05.2025. 10:16 ] @
1 je svodljivo na 2 jer su trrigonometrijske funkcije samo geometrijske definicije koje se opravdavaju geometrijskim teoremama i osobine trigonometrijskih funkcija su geometrijske teoreme.
Uvek se možemo praviti blesavi i ne zvati trigonmetrijske funkcije njihovim imenima, nego njihove definicije i osobine provlačiti kroz geometrijski dokaz.
[ jans @ 11.05.2025. 17:20 ] @
Nedeljko je napisao:
„... Uvek se možemo praviti blesavi i ne zvati trigonmetrijske funkcije njihovim imenima, nego njihove definicije i osobine provlačiti kroz geometrijski dokaz.“
Neki bi rekli, nije šija nego vrat.
Drugim rečima, neki geometrijski zadaci u kojima figurišu uglovi, primenom 2. načina ne mogu da se reše.
[ Nedeljko @ 12.05.2025. 05:05 ] @
Imaš li ti logičku formulaciju pravila igre? Šta je dozvoljeno, a šta ne?
Trigonometrijske funkcije su primena stavova o siičnosti i podudarnosti.
Transformišeš dokaz trigonometrijskim funkcijama u dokaz pomoću sličnosi i podudarnosti.
[ jans @ 12.05.2025. 23:54 ] @
U prvoj poruci u ovoj temi, u opisu 2. načina rešavanja geometrijskih zadataka nisam bio dovoljno precizan. Izostavio sam deo za koji sam smatrao da se podrazumeva. Izvinjavam se zbog toga.
Jasno mi je, o tome si i ranije pisao, da dokaz pomoću trigonometrijskih funkcija može da se transformiše u dokaz pomoću sličnosti i podudarnosti. To znači da zadatak najpre rešimo pomoću trigonometrije a onda to rešenje transformišemo. U transformisanom rešenju ( formalno ) nema trigonometrije, a možda se i ne vidi da je trigonometrija korišćena. Međutim, iako u transformisanom rešenju nema trigonometrije, da bi do tog rešenja došli, koristili smo trigonometriju. To je činjenica koju nisam eksplicitno iskazao u opisu 2. načina rešavanja geometrijskih zadataka, i na to sam mislio kada sam u drugoj poruci napisao „neki geometrijski zadaci u kojima figurišu uglovi, primenom 2. načina ne mogu da se reše“.
[ Nedeljko @ 13.05.2025. 07:19 ] @
Ako rešenje tako transformišemo, onda smo do njega zaista došli korišćenjem trigonometrije. Izgleda da si dobar matematičar.
Međutim, na osnovu čega tvrdiš da ako je rešenje pomoću sličnosti i podudarnosti formalno moguće, da se do njega ne može doći na drugi način, bez trigonometrije? Takav dokaz svejedno "miriše" na trigonometriju, pa ako bi neko došao na ideje preko kojih se dolazi do trigonometrije, mogao bi da ga reši. Ako je moguć takav dokaz, zašto ne bi bio moguć oi drugačiji koji ne "miriše" na trigonometriju?
Ovakvi stavovi se dokazuju upravo svođenjem jedne vrste dokaza na druge vrste. Ako je dokaz neke vrste formalno moguć, ko može da tvrdi da se do toga nije moglo doći bez transformisanja neke druge vrste dokaza?
Ja ovde insistiram na razumevanju veze između različitih delova matematike. Postoji razlog zašto je funkcija jednaka [tex]\sum_{n=0}^\infty(-1)^n\frac{x^{2n+1}}{(2n+1)!}[⁄tex] primenljiva u geometriji. To je suštinski razlog zašto je ta primena korektna i naravno da ima formalno opravdanje.
P. S. Ne znam zašto TeX ne radi.
[ Nedeljko @ 13.05.2025. 07:51 ] @
Da bi se formalno ispitalo da li je uvek moguć dokaz koje ne "miriše" na trigonometriju, potrebna je formalizacija, kao što intuicionistička formalizacija matematike daje odgovore na pitanja šta je nemoguće rešiti konstruktivno. Postoje i druge takve formaliyacije. Ovde bi bila potrebna neka koja iybegava ideje koje vode to trigonometrije, odnosno u kojoj trigonometrija nije moguća.
[ miki069 @ 14.05.2025. 07:14 ] @
U zadatku koji je povod za ovu temu nije tražena konstrukcija ugla od 50, već samo da se otkrije/dokaže da je 50.
Ugao od 150 se može konstruisati.
Ugao od 50 se ne može konstruisati.
U trigonometrijskom rešenju je korišćen tangens trostrukog ugla to jest tg(150) = tg(3*50) = ...
Da se tu ne krije problem rešavanja ovog zadatka euklidskom geometrijom?
[ Nedeljko @ 14.05.2025. 14:48 ] @
Ne krije se nigde. I ta formula je posledica stavova o sličnosti i podudarnosti.
[ jans @ 15.05.2025. 23:51 ] @
Citat: Nedeljko:
Međutim, na osnovu čega tvrdiš da ako je rešenje pomoću sličnosti i podudarnosti formalno moguće, da se do njega ne može doći na drugi način, bez trigonometrije?
Ne mogu to da tvrdim zato što nemam dokaz. To je samo hipoteza. Trebalo bi, u drugoj poruci na kraju rečenice „Drugim rečima, neki geometrijski zadaci u kojima figurišu uglovi, primenom 2. načina ne mogu da se reše.“, umesto tačke staviti znak pitanja.
I još nešto. Čini mi se da je potrebna još jedna napomena.
Kada sam u navedenim temama postavio pitanje rešivosti tih zadataka pomoću Euklidske geometrije ( naravno bez trigonometrije, pošto je rečeno da se zadaci mogu rešiti pomoću trigonometrijskih funkcija ), mislio sam na geometriju koja se izučava u srednjoj školi. ( Mislim da je to i Miki tako shvatio. Zaključio sam to iz njegovih poruka. )
[ Nedeljko @ 16.05.2025. 01:27 ] @
Pa, u sednjoj školi se uče stavovi o sličnosti i podudarnosti. Sve što je rešivo trigonometrijom je svodljivo na njih.
[ jans @ 18.05.2025. 23:57 ] @
Citat: Nedeljko: Pa, u sednjoj školi se uče stavovi o sličnosti i podudarnosti. Sve što je rešivo trigonometrijom je svodljivo na njih. Nije mi jasno kako to primeniti u zadacima.
Navešću jednostavan zadatak:
"Date su dve stranice trougla b=5 i c=6, i ugao 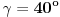 . Odrediti ugao beta."
Zadatak se lako rešava pomoću sinusne teoreme. Rešenje je 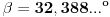 .
Međutim, nemam predstavu kako bi ovaj zadatak mogao da se reši pomoću Euklidske geometrije, odnosno geometrije koju smo učili u srednjoj školi, a da ne koristimo trigonometriju.
[ Nedeljko @ 20.05.2025. 23:59 ] @
Koeficijent pravca ugla od 45 stepeni je 1. Za ugao sa koeficijentom pravca k možemo izračunati koeficijent pravca polovine ugla. Ako je s koeficijent pravca polovine ugla, onda je 2s/(1-s^2)=k, odakle se rešavanjem kvadratne jednačine izražava s preko k.
Lako se izračunavaju sinus i kosinus ugla sa koeficijentom k. Tako dobijamo sinus i kosinus ugla oblika 45 stepeni podeljeno sa dovoljno velikim stepenom dvojke.
sin(x) i cos(x) su u vezi sa rotacijom oko koordinatnog početka koja tačku (1,0) slika u tačku (cos(x),sin(x)). Preslikavanjem tačke (cos(y),sin(y)) dobijamo adicione formule.
Tako dobijamo sinuse i kosinuse uglova oblika ceo broj puta 45 stepeni, pa podeljeno sa stepenom dvojke, a to je gust skup, što nam omogućava računanje uglova i njihovih sinusa sa željenom tačnošću.
Naravno, sve ovo sa trigonometrijom se kamuflira u sličnost i podudarnost.
[ jans @ 25.05.2025. 00:32 ] @
Jasno mi je to što si napisao u poslednjoj poruci, o tome si govorio i u prethodnim postovima. U svakom slučaju, hvala za objašnjenja.
I još jedno pitanje. Da li je zadatak naveden u mojoj prethodnoj poruci moguće rešiti pomoću Euklidske geometrije, odnosno geometrije koju smo učili u srednjoj školi, a da ne koristimo ni trigonometriju, ni kamufliranu trigonometriju, ni analitičku geometriju ( zbog koeficijenta pravca prave i ugla između pravih ), drugim rečima elementarno?
[ Nedeljko @ 25.05.2025. 10:33 ] @
Koeficijent pravca je količnik kateta nekog pravouglog trougla, a što se kamuflaže tiče...
Za to ti treba formalizacija koja ne omogućava definisanje trigonometrijskih funkcija. To će biti vrlo siromašna matematika.
Matematika je povezana.
[ jans @ 27.05.2025. 21:34 ] @
Znam da je koeficijent pravca količnik kateta nekog pravouglog trougla, ali takođe znam da je taj količnik i tangens jednog oštrog ugla u tom trouglu. Ako koristimo taj količnik kateta, koristimo kamufliranu trigonometriju. Možemo zadatak rešavati pomoću količnika stranica pravouglog trougla koristeći sličnost i podudarnost trouglova, i na kraju dobiti odgovarajući količnik karakterističan za nepoznati ugao. A onda, pošto ne koristimo trigonometriju i inverzne trigonometrijske funkcije, treba odrediti, pomoću numeričke analize, koji to ugao u nekom pravouglom trouglu ima isti karakterističan količnik kao nepoznati ugao, ili proveriti u unapred pripremljenim tablicama karakterističnih količnika oštrih uglova. Međutim, ne vidim svrhu ovakvog postupka koji je i duži i složeniji od postupka sa trigonometrijom. Naravno, možemo i tako rešavati zadatak, ali opet je to kamuflirana trigonometrija.
Još jednom napominjem da sam, kada sam u navedenim temama napisao da mi nije poznato da li je moguće zadatke u tim temama rešiti Euklidskom geometrijom, mislio na geometriju koju smo učili u srednjoj školi, geometriju bez trigonometrije (i bez kamuflirane trigonometrije i analitičke geometrije), odnosno rešiti elementarno. Kao ilustracija za takav način rešavanja može poslužiti i zadatak u temi koju je postavio Miki: Zašto mrzim (volim) geometriju.
Zadatak je rešen na nekoliko načina, a elementarno rešenje je rešenje člana Milosh Milosavljevic1. [ Nedeljko @ 28.05.2025. 00:12 ] @
Citat: jans: A onda, pošto ne koristimo trigonometriju i inverzne trigonometrijske funkcije, treba odrediti, pomoću numeričke analize, koji to ugao u nekom pravouglom trouglu ima isti karakterističan količnik kao nepoznati ugao, ili proveriti u unapred pripremljenim tablicama karakterističnih količnika oštrih uglova.
Pročitaj pažljivo ovu moju poruku.
Citat: jans: Međutim, ne vidim svrhu ovakvog postupka koji je i duži i složeniji od postupka sa trigonometrijom. Naravno, možemo i tako rešavati zadatak, ali opet je to kamuflirana trigonometrija.
Upravo je u tome suština. Definicije ne smeju biti kreativne, što znači sledeće:
1. Svaki iskaz u kome se koristi definisani pojam je ekvivalentan nekom iskazu u kome se ne koristi definisani pojam, s tim da se dokay ekvivalencije iyvodim korišćenjem definicije.
2. Za svaki iskaz u kome se ne koristi definisani pojam koji je dokaziv korišćenjem definisanog pojma važi da je dokaziv i bez definisanog pojma.
Ne sme definicija da proizvodi zaključke u kojima se definisani pojam ne pojavljuje, a do kojih se nije moglo doći bez definisanog pojma. Definisije služe samo da skrate i pojednostave stvari, a ne da proizvedu nešto suštinski novo što bez njih nije bilo moguće. Naravno da su vrlo korisne.
To važi i za definicije trigonometrijskih funkcija.
Citat: jans: Naravno, možemo i tako rešavati zadatak, ali opet je to kamuflirana trigonometrija.
To je rešenje dobijeno od drugog rešenja postupkom eliminacije definicija.
Citat: jans: Još jednom napominjem da sam, kada sam u navedenim temama napisao da mi nije poznato da li je moguće zadatke u tim temama rešiti Euklidskom geometrijom, mislio na geometriju koju smo učili u srednjoj školi, geometriju bez trigonometrije (i bez kamuflirane trigonometrije i analitičke geometrije), odnosno rešiti elementarno.
Eliminacijom definisanih pojmova dobijaš rešenje koje ne koristi te pojmove. Možeš to nayivati kamuflažom, ali je činjenica da definicije trigonometrijskih funkcija nisu kreativne. U suprotnom ne bi bile korektne. [ jans @ 12.06.2025. 23:27 ] @
Nedeljko, u redu je i razumem to što si napisao, iako u poslednjoj poruci ima delova koje bi trebalo razjasniti. Možda drugi put.
Međutim, smatram da smo se malo udaljili od Mikijevog pitanja, odnosno da nismo odgovorili na to pitanje. Da podsetim. Miki je u jednoj od poruka napisao: Citat: Nedeljko jasno je da važi stav:
Ako je zadatak rešiv Euklidskom geometrijom sigurno je rešiv i trigonometrijom.
Nisam siguran da važi i obrnuto.
Objasniću kako sam ja shvatio Mikijevu konstataciju da je „ zadatak rešiv Euklidskom geometrijom “.
Pošto je zadatak koji je Miki postavio u temi Zašto mrzim (volim) geometriju, na nekoliko načina rešen pomoću trigonometrije, Miki je u jednoj od poruka napisao: Citat: Ajde sad neko da ga uradi čisto geometrijski, bez trigonometrije. U narednoj poruci, postu koji je postavio član Milosh Milosavljevic1, izloženo je takvo rešenje. Miloš ga je nazvao elementarno rešenje. To rešenje je dobijeno pomoću Euklidske geometrije, geometrije koju smo učili u srednjoj školi, ali bez korišćenja trigonometrije ( i bez analitičke geometrije, rešenje koje nije transformisano trigonometrijsko rešenje – rešenje koje nije, ti si ga nazvao, kamuflirano trigonometrijsko rešenje ). Rešenje u kojem se ne koriste ni približna izračunavanja.
Prema tome, ako treba da odredimo nepoznati ugao u rešivom geometrijskom zadatku u kojem figurišu i uglovi, interesuju nas dva načina rešavanja:
1.) elementarno rešavanje;
2.) rešavanje pomoću trigonometrije ( koju koristimo direktno ili posredno ).
Vratimo se sada na prvi citat u ovom postu, odnosno na rečenicu „Nisam siguran da važi i obrnuto. “ Drugačije rečeno, Miki smatra da neki od zadataka koji su rešivi pomoću trigonometrije, mogu da se reše i elementarno, a neki verovatnono ne.
To je Mikijevo mišljene, odnosno stav za koji nije rečeno da li je ispravan ili nije ispravan.
[ Nedeljko @ 13.06.2025. 22:52 ] @
Trigonometrija se izvodi iz tog elementarnog, tako da se trigonometrijsko može transformisati u elementarno.
E, sad, rešenje dobijeno takvom transformacijom će biti vrlo dugo.
Kako definišemo euklidsku geometriju?
Ako euklidsku geometriju definišemo preko npr. aksiomatskog sistema Borsuka i Šmileve, onda se yadatak svodi na to da se dokaže da neko tvrđenje važi u svim modelima.
Teorema je da taj aksiomatski sistem ima tačno jedan model do na izomorfizam - R3 i onda se dokayivanje svodi na dokayivanje tog stava u tom jednom modelu.
Rekao bih da se niste srodili sa formalnom matematičkom veyom iymeđu analiye i geometrije. Sa trigonometrijom iloi bez nje - to je isto. Skup posledica je isti.
[ jans @ 18.06.2025. 22:38 ] @
Nedeljko izvini, nije mi jasno zašto prebacuješ diskusiju na, kako bi neki rekli, viši level.
Niko ovde ne osporava povezanost matematike, niti negira mogućnost transformacije trigonometrijskog u elementarni dokaz. Ja mislim da je dobar deo onih učenika, koji su u gimnaziji ili nekim stručnim školama solidno savladali gradivo matematike, još u srednjoj školi shvatio koliko je matematika povezana. A ako sam napisao da ne vidim svrhu transformisanja trigonometrijskog dokaza, razlog je isti onaj koji i ti navodiš. Takav dokaz bi bio predugačak. A to bi bilo u stilu „ umetnost radi umetnosti “.
Pitanje se ne odnosi ni na formalizaciju geometrije, niti na automatizaciju dokazivanja u geometriji. Pitanje je da li je moguće, zadatak u kojem treba odrediti nepoznati ugao, zadatak koji je rešiv pomoću trigonometrije, rešiti elementarno, čisto geometrijski bez trigonometrije. Onako kako je zadatak u temi "Zašto mrzim (volim) geometriju" rešio Milosh Milosavljevic1 ( na forumu ima i drugih zadataka koji su rešeni na sliča način). Za takvo rešavanje je dovoljna srednjoškolska geometrija bez trigonometrije, a često je dovoljno gradivo osnovne škole, pa takav postupak mogu da razumeju ( a neki i da primene ) i učenici koji su završili osnovnu školu.
[ Nedeljko @ 19.06.2025. 04:42 ] @
Kada se postavi pitanje "da li je moguće", tu se ne postavljaju ograničenja dužine i složenosti. Pitanje je da li postoji niz koraka koji ispunjava neke uslove.
Da, postoji. Transformacijom trigonometrijskog dokaza se dobija takav niz. To je ono što je objektivno.
Da li je moguće "onako kako je osoba A rešila zadatak B"? Pa, ne, jer ono što je napisala osoba A kao rešenje zadatka B odgovara samo zadatku B, a ne i nekom drugom zadatku C.
Pitanje koje si postavio je neodvojivo od pitanja kriterijuma.
I ne, gimnazijksa matematika (pa i većina fakultetskih) ne omogućava da se razume u kakvoj su vezi stepeni red koji se uči kao razvoj sinusa sa odnosom dužina ivica u pravouglom trouglu u euklidskoj geometriji. Ova rasprava je samo posledica tog nerazumevanja.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|