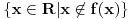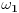Pitanje merljivosti skupa nema nikakve veze sa njegovom ograničenošću. Štaviše, skup je merljiv ako i samo ako je prebrojiva unija ograničenih merljivih skupova. To važi i za merljivost u smislu Borela i u smislu Lebega. No, Kantorov skup je skup Borelov kao zatvoren, pa se čak nalazi na najnižem spratu hijerarhije Borelovih skupova.

Lebeg nemerljiv skup se i ne može konstruisati, već se može samo dokazati njegova egzistencija. Naime, postoje modeli teorije skupova u kiojima važe sve aksiome teorije skupova izuzev aksiome izbora, aksioma zavisnog izbora (DC) koja glasi

Za svaku relaciju R na nepraznom skupu A sa osobinom da za ma koji element x skupa A postoji element y skupa A za koji važi xRy, postoji beskonačan niz a_n takav da za svako n važi a_nRa_n+1

i tako da u tom modelu važi tvrđenje "Svi podskupovi od Rⁿ su Lebeg merljivi". To upravo znači da se svi dokazi postojanja Lebeg nemerljivih skupova oslanjaju na aksiomu izbora, pa su nekonstruktivni.

No, sa Borel merljivim skupovima već nije tako. Naime, bez aksiome izbora se dokazuje da Borel merljivih skupova ima "samo" kontinuum mnogo, dok podskupova od R ima više (po Kantorovoj teoremi partitivnom skupu), pa mora biti Borel nemerljivih skupova. Sve to ne zavisi od aksiome izbora, pa nam ostaje nada da se Borel nemerljiv skup može konstruisati.

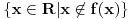
Mihail Suslin je konstruisao čak analitički skup (neprekidna slika Borelovog) koji nije Borelov. No, nećemo ići tako daleko. Da bi se konstruisao skup koji nije Borelov dovoljno je konstruisati surjekciju f skupa realnih brojeva na skup Borelovih podskupova od R. Tada skup neće biti Borelov.

Za to ti je neophodno da znaš da konstruišeš bijekciju između skupova A i B ako imaš injekcije u oba smera, bijekcije između skupa R, skupa svih beskonačnih nizova prirodnih brojeva, skupa svih beskonačnih realnih nizova skupa R² i da pratiš kumulativnu hijerarhiju Borelovih skupova.

Najpre konstruišeš surjekciju skupa R na skup otvorenih skupova kao prebrojivih unija otvorenih kugli poluprečnik 1/n sa racionalnim centrima (prebrojiva baza). To je ona bijekcija između R i skupa svih beskonačnih nizova prirodnih brojeva. Sada možeš da konstruišeš i surjekciju skupa R na skupa svih zatvorenih podskupova od R, kao i surjekciju skupa R na skup svih otvorenih ili zatvorenih podskupova od R. Time se rešavamo prvog sprata hijerarhije Borelovih skupova.

Na svaki sledeći sprat se penješ praveći surjekciju između R i prebrojivih unija i preseka skupova sa prethodnih spratova. Tu se koristi bijekcija između skupa R is skupa svih beskonačnih nizova realnih brojeva.

U graničnom slučaju se koristi činjenica da je prebrojiva unija skupova moći kontinuum takođe skup moći kontinuum. Tu takođe možeš koristiti bijekciju između skupa R i skup svih beskonačnih realnih nizova.

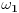
Ostaje ti još samo da R preslikaš surjektivno na najmanje neprebrojivo uređenje (ordinal jer hijerarhija Borelovih skupova ima tu visinu. Tu ti treba bijekcija između skupa R i skupa svih podskupova od NxN. Sada se treba setiti da je pomenuto uređenje izomorfno sa preduređenjem svih najviše prebrojivih dobrih uređenja posečenim tako da bude uređenje. E, ta najviše prebrojiva uređenja su podskupovi od NxN. Na kraju treba pomoću ove surjekcije povezati sve spratove u jednu celinu.


Nadam se da ćeš se snaći na osnovu ove skice.

ovo je super nedeljko.. hvala..
sad su mi neke stvari dosle na svoje mjesto..

nego, mozes li mi preporuciti neku knjigu koja se bavi ovom problematikom? ja imam aljancica (uvod u realnu i funkcionalnu analizu) i branislava mirkovica (teorija mera integrala)?

Ne znam na koju konkretno problematiku misliš. Ako to nije teorija mere, već ovakve zavrzlame oko Borelovih i analitičkih skupova, u njih ti može biti uvod na primer Teorija Skupova od Mostovskog i Kuratovskog. Dosta je stara, ali može da posluži za početak. Teoriju mere mislim da je dobro obradio Halmoš.

No, ovu moju konstrukciju nećeš tamo naći. To je moje jutrošnje razmišljanje o tvom problemu.

Kao udzbenik za analizu III na MF-u koristili smo Teorija mere, funkcionalna analiza, teorija operatora od Arsenovicca, Dostanicca i Jocicca. Mozze lepo da posluzzi za uvod u teoriju mera.

Dizdar je rekla da već ima Aljančića i Branislava Mirkovića, a pogotovu u Mirkoviću ima mnogo više o meri nego u knjizi koju pominješ. Tako da ne vidim kako bi ta knjiga mogla da dopuni sadržaje o meri iz Aljančića i Mirkovića. Ako vlada engleskim, onda je Walter Rudin - Real and complex analysis daleko bolje rešenje za savladavanje sadržaja iz te knjige, naročito uz knjigu Functional analysis istog autora. Ako je zanima samo teorija mere, onda je Halmoš možda i najbolji izbor.

Meni se ipak čini da nju zanima nešto drugo. Konstrukcije skupova kojijesu ovakvi, a nisu onakvi. To će naći u knjigama koje obrađuju ne teoriju mere, već deskriptivnu teoriju skupova. Knjigu koju pominješ će morati da koristi za polaganje ispita iz Analize III, ali ovo što je ona pitala ipak pripada drugoj problematici.

Shvatio sam da je zanima teorija mere.
Pomenuta knjiga je predlog kao uvod u teoriju mere, svakako da je Mirkovicc opshirniji. Naravno da su te knjige na engleskom odlichan izbor.

ma generalno me zanima sve vezano za realnu i furieovu analizu.. a teorije mjera su ono gdje mi je najvise stvari falilo.. nisu mi slozene..etc.etc..
kupila sam Rudina, odlicna knjiga...

e sad sam vec malo dosadna, al moram da pitam.. naime, dobila sam diplomsku radnju na temu iterpolacioni polinomi.. ne zanima me numericka primjena, nego interpolacioni polinomi opet iz perspektive realne, funkcionalne i furieove analize..
mentorova preporuka je adams.. jel postoje neke knjige na srpskom gdje imam detaljniji uvod u Lp prostore, interpolazione polinome i primjenu istih... mogu i knjige na engleskom, pa cak i na ruskom, al bih rado nesto za lagano citanje citala na meni 100%razumljivom jeziku..

Reci mi gde stuiraš ako nije tajna. Što se tiče realne i Furijeove analize, koliko je meni poznato, oni se ne povezuju sa interpolacionim polinomima, već sa ortogonalnim polinomima, kao što su Lagranževi, Čebiševljevi itd., tako da pre svega treba raščistiti oko toga šta tebi zapravo treba.

Lp prostore imaš u Rudinu, Aljančiću i pomenutom udžbeniku Analize III na Matematičkom Fakultetu u Beogradu. Moja najtoplija preporuka je Rudin, ne samo zato što je najbolje obradio problematiku, već i da bi vežbala engleski, koji će ti svakako trebati. Koristi takođe i internet i mašine za pretraživanje.

am.. sarajevski univerzitet...mada nisam najreprezentativniji student... vratila sam se studiju poslije dvije godine nestudiranja..etc..etc...
ma sad si me kroz zbunio... tema se zaista zove interpolacioni polinom, glavni teorem kojim se bavim je interpolacioni teorem marcinkevicha.. zasniva se na slabim operatorima u Lp prostorima.. i to je otprilike to..
ko izdaje tu analizu III na beogradskom matematickom fakultetu? kako bih ja to mogla nabaviti? ima li neki site, il nesto slicno.. ono moram li doci u bg, il mogu naruciti knjigu? bila sam na sajmu knjiga u oktobru u beogradu, al tu knjigu nisam primjetila..tad sam kupila teoriju mera integrala...

Lično mislim da pomenuti udžbenik nije vredan tolikog "cimanja". Njega sam pomenuo misleći da si negde blizu Beograda, recimo u Novom Sadu (pošto na Matematičkom Fakultetu u Beogradu ne postoji diplomski rad). Zato sam pitao gde studiraš, a ne da bih te preslišavao. To što si pauzirala nema nikakve veze. Lp prostore ćeš naći u svakom udžbeniku Funkcionalne Analize. Slobodno pročešljaj sarajevsku biblioteku, pri čemu ja ipak mislim da je Rudin najbolji izbor i zbog Matematike i zbog jezika. Na kraju krajeva, konsultuj se sa svojim mentorom.