Prošli put su se potkrale neke greške, pa hajde da ih ispravim.
Neka je

skup tačaka u
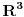
koji ima osobinu da je presek bilo koje ravni i skupa

prazan skup, tačka, prava, unija dve paralelne prave, unija dve prave koje se seku, elipsa, parabola ili hiperbola. Dokažimo da postoje konstante A,B,C,D,E,F,G,H,I,J da za ma koje realne brojeve x,y,z važi
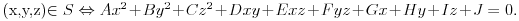
Pretpostavimo najpre da svaka ravan u preseku sa skupom

daje prazan skup, tačku ili pravu. Tada su sve tačke skupa

kolinearne, pa ako uočimo ravan na kojoj leži prava kojoj pripadaju sve tačke skupa

, presek skupa

sa tom ravni će biti skup

, pa je

ili prazan skup ili tačka ili prava. U sva tri slučaja skup

ima jednačinu traženog oblika. Prazan skup ima jednačinu
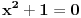
, tačka
jednačinu
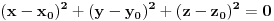
, a prava
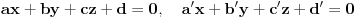
jednačinu
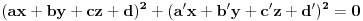
.
Pretpostavimo zato da postoji ravan koja u preseku sa skupom

ne daje niti prazan skup, niti tačku, niti pravu. Budući da svaka od preostalih figura ima tačno dve zajedničke tačke sa barem jednom pravom, postoje različite tačke

i

skupa

sa osobinom da na pravoj
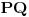
nema drugih tačaka skupa

. Izaberimo Dekartov pravougli koordinatni sistem sa koordinatnim početkom u tački

kome je

-osa prava
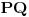
. Dakle, koordinate tih tačaka su
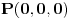
i
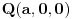
za neko
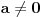
. Ukoliko dokažemo da u tom Dekartovom pravouglom koordinatnom sistemu skup

ima jednačinu tog oblika, onda je on ima i u svakom drugom.
Sa
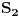
označimo skup svih parova realnih brojeva
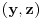
, takvih da tačka
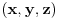
pripada skupu

za tačno dve realne vrednosti

. Neka par
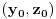
pripada skupu
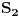
. Presek skupa

i ravni
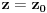
ne može biti u prazan skup, tačka ili prava, pa mora biti unija dve prave koje se seku ili unija dve paralelne prave ili elipsa ili parabola ili hiperbola. Prava
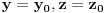
ima sa tim presekom tačno dve zajedničke tačke. Stoga postoji otvoreni interval

takav da
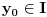
i da za ma koje
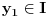
prava
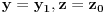
ima sa tim skupom tačno dve zajedničke tačke. No, to upravo znači da par
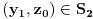
za svako
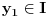
, tj. da je
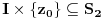
. Na sasvim sličan način se dokazuje da postoji otvoren interval

takav da
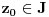
i da je

.
Neka je
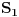
skup svih realnih brojeva

takvih da postoji realan broj

tako da par
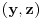
pripada skupu
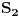
. Prema prethodnim razmatranjima skup
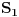
je otvoren, tj. oko svake njegove tačke možemo opisati okolinu koja je cela u tom skupu. Naime, za ma koje
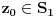
postoji takvo
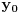
takvo da
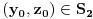
, pri čemu za otvoren interval

takav da
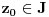
i

važi
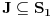
. Pritom,
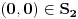
i
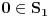
zbog načina na koji smo izabrali tačke

i

i Dekartov pravougli koordinatni sistem.
Neka
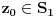
. Presek skupa

i ravni
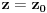
ima jednačinu oblika
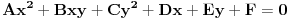
pri čemu koeficijenti zavise od
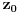
. Ako je
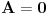
, onda ne postoji
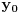
takvo da
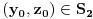
, što je u suprotnosti sa
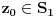
. Stoga je
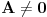
, pa delenjem jednačine sa

dobijamo ekvivalentnu jednačinu istog oblika u kome je koeficijent uz

jednak jedinici. Stoga presek skupa

i ravni
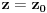
ima jednačinu
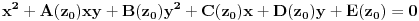
za neke funkcije
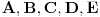
definisane na skupu
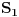
.
Neka
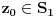
. Izaberimo različite realne brojeve
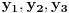
takve da parovi
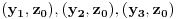
pripadaju skupu
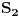
. Postoje otvoreni intervali
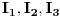
kojima pripada
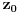
takvi da za svako

iz
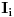
par
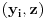
pripada skupu
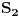
. Neka je

presek tih intervala.

je otvoren interval kome pripada
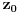
i takav da za svako
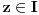
važi
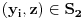
, a samim tim i
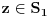
. Dakle,
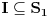
.
Posmatrajmo presek skupa

sa ravni
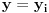
. Za svako

iz intervala

postoje tačno dve vrednosti za

takve da
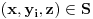
, pa jednačina preseka ima oblik
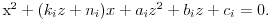
No, budući da ova jednačina po

ima ista rešenja kao jednačina
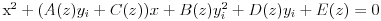
na osnovu Vijetovih formula zaključujemo da važi
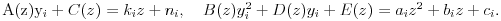
Odatle dobijamo matrične jednačine
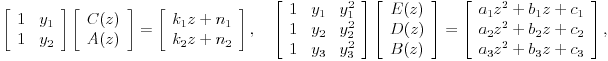
koje važe za sve
. No, determinante tih sistema su različite od nule (Vandermondove su) i konstantne. Recimo, determinanta drugog sistema je jednaka

. Odatle i iz Kramerovog pravila sledi da su funkcije
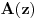
i
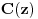
linearne, a funkcije
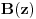
,
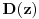
i
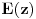
najviše kvadratne. Naravno, sve to važi na intervalu

. Odatle sledi da skup

u pojasu
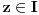
ima jednačinu oblika
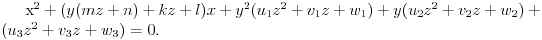
No, za svako

ravan
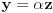
seče skup

po uniji dve paralelne prave ili uniji dve prave koje se seku ili po elipsi ili po paraboli ili po hiperboli jer preseku pripadaju tačke

i

pri čemu preseku ne pripada ni jedna druga tačka prave
. Stoga jednačina preseka u našem pojasu glasi
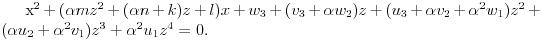
Ali takav presek ima jednačinu oblika
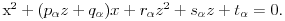
Te jednačine za svako

imaju tačno dva rešenja po

za sve

iz nekog otvorenog intervala
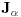
kome pripada nula. Pritom, možemo pretpostaviti da je
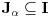
za svako

. Pošto za svako

i za sve
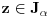
ta jednačina po

imatju ista rešenja, iz Vijetovih formula zaključujemo da za svako

i svako
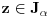
važi
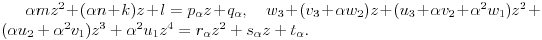
No, kako za svako

interval
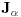
sadrži beskonačno mnogo tačaka, odatle sledi da za svako

važi
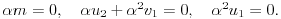
Birajući dve različite vrednosti za

ali i različite od nule, slično kao i ranije zaključujemo da važi
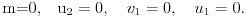
Odatle, i na osnovu odgovarajuće jednačine u pojasu
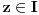
dobijamo da skup

ima jednačinu traženog oblika u tom pojasu. Neka je
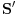
skup tačaka određen istom tom jednačinom drugog reda, ali u celom prostoru. Dokažimo da je
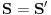
. Neka je

proizvoljna tačka i

ravan kojoj pripadaju tačke

,

i

. Budući da se skupovi

i
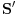
poklapaju u pojasu
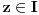
, presek te ravni sa skupom

će biti u tom pojasu isti kao i sa skupom
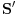
. Setimo se da tačke

i

pripadaju tom preseku, ali da mu ne pripada niti jedna druga tačka prave
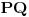
. Budući da znamo da je taj presek unija dve paralelne prave ili unija dve prave koje se seku ili elipsa ili parabola ili hiperbola i budući da je takva figura u potpunosti određena svojom slikom u bilo kojoj okolini takvih svojih dveju tačaka, presek te ravni sa skupovima

i
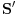
je isti, pa tačka

ili pripada i jednom i drugom ili nijednom od njih. Budući da je tačka

potpuno proizvoljna, skupovi

i
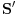
su jednaki, čime je tvrđenje u potpunosti dokazano.
Edit: Ispravka greške.
[Ovu poruku je menjao Nedeljko dana 12.12.2012. u 22:32 GMT+1]