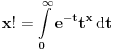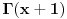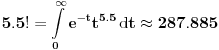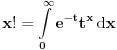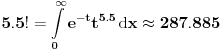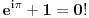[ darkosos @ 12.05.2004. 14:57 ] @
|
| Nisam izdržao, ipak malo preteruju sa ovim zadacima. Elem:
Dat je pravougaonik ABCD u kome je BC=2AB. Na stranici BC je data tačka M takva da je ugao AMD jednak uglu CMD. Odrediti te uglove.
Inače nije ovo najgore. Ima dokazivanja u vezi iracionalnih brojeva i koječega što je ipak malo preterano kao zadatak za prijemni, koji bi trebao da predstavlja presek gradiva... Ne mogu da zamislim đaka osnovne škole, osim ako nije izrazito nadaren i/ili ima iskustva sa problemskim zadacima (kroz takmičenja itd.), koji sam rešava ovakve zadatke. Ostaje im samo da nabubaju i cela stvar gubi smisao. Pa većina njih neće znati ni da nacrta!
Inače, zadatak je simpatičan i nije toliko težak, pa može doneti radost ;) |
[ zzzz @ 16.05.2004. 01:22 ] @
Nebih rekao da je ovo teško.Prosječan učenik sedmog razreda zna
da je zbir uglova u trokutu 180 stepeni.Takođe i da su, kod istokračnog
trougla,nasuprot jednakim stranicama uglovi jednaki.
Dakle:najprije skica pa onda zaključak da je ugao MDC=90-ugao CMD.
Odatle ispade i da je ugao ADM=uglu AMD.
Zaključi da je trokut AMD istokračan, pa povuče luk iz D (sa centrom
u A ) na stranicu BC.Prosječan đak to riješava za 10 min.
[ darkosos @ 16.05.2004. 08:25 ] @
Citat:
zzzz:
Prosječan đak to riješava za 10 min.
Milane, verovatno nikad nisi držao časove "prosečnom" đaku :) Ma nema šanse ni da nacrta a kamoli da izvede tri-četiri zaključka zaredom, vodeći se ni za čim. Prosečan đak razmišlja "kako da izračunam taj ugao kad mi ništa nije dato" ;) Veruj mi, držim časove već više od 12 godina.
[ Srdjan Marinkov @ 24.08.2008. 22:02 ] @
Mozda nema mnogo veze sa temom, ali ajd' da to ovde napisem...
Pre par dana sam pomagao jednom decku da spremi popravni iz mehanike za prvu godinu srednje skole. Nista posebno, osnove statike (sile, grede, momenti i sl.) Razumem neko ko ide na popravni u u prvoj godini srednje skole da nema mnogo veze sa gradivom, ali kako sam poceo sa njim da radim, vidim da cu prvo morati da ga naucim sta je to sinus a sta cosinus, pa posle vidim da nikad nije cuo za Pitagorinu teoremu, pa kako smo dalje "radili" vidim da nezna ni razlomke (npr. x/7=11, x=?) i kao vrhunac, nezna ni decimalne brojeve (npr 0,55x10=?) KATASTROFA!!!
Neznam kako, on je imao dvojku iz matematike, a popravni mi je javio pre par dana da je polozio!
Pricam posle toga sa komsijom koji predaje u srednjoj elektrotehnickoj skoli i on me uverava da to nije nista, jer je njemu 99% ucenika takvo. Npr. kaze mi da u jednom drugom razredu srednje (cetvrti stepen) NI JEDAN ucenik nije znao da sabere koliko je 5-2x10-3
Prosto, ne mogu da verujem da je to moguce!!?
[Ovu poruku je menjao SrDJaNN dana 26.08.2008. u 07:58 GMT+1]
[ R A V E N @ 25.08.2008. 13:10 ] @
Je li na tabli ili u kontrolnom radu?
Učenici su obično neradi da idu na tablu,čak i kad znaju nešto.
[ djordje1979 @ 26.08.2008. 02:31 ] @
Citat:
SrDJaNN:Npr. kaze mi da u jednom drugom razredu srednje (cetvrti stepen) NI JEDAN ucenik nije znao da sabere koliko je 5-2x10
-3!
Prosto, ne mogu da verujem da je to moguce!!?
Faktorijel decimalnog broja se ne radi u srednjoj skoli definitivno. Dal ne preterujete...
[ Srdjan Marinkov @ 26.08.2008. 06:58 ] @
Zank uzvika je u ovom slucaju interpunkcija tj. moje cudjenje, a ne faktorujel. Ispravio sam...
[ igorpet @ 26.08.2008. 09:45 ] @
Citat:
djordje1979: Faktorijel decimalnog broja se ne radi u srednjoj skoli definitivno. Dal ne preterujete...
A gde se radi faktorijel decimalnog broja?
Nesto ne znam da sam ikada video faktorijel decimalnog broja (mozda gresim, pa rekoh da pitam)!
Ako je 5!=120 koliko bi bilo npr 5,5!=?
[ Bojan Basic @ 26.08.2008. 10:12 ] @
Citat:
igorpet:
Ako je 5!=120 koliko bi bilo npr 5,5!=?
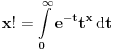
(Poslednji integral obeležava se sa
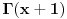
, što ima svoje razloge.)
Dakle,
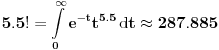
. Ista formula koristi se i za kompleksne vrednosti.
[Ovu poruku je menjao Bojan Basic dana 26.08.2008. u 13:39 GMT+1][ petarm @ 26.08.2008. 10:29 ] @
Citat:
Bojan Basic:
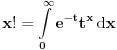
(Poslednji integral obeležava se sa
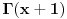
, što ima svoje razloge).
Dakle,
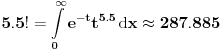
. Ista formula koristi se i za kompleksne vrednosti.
Samo mala ispravka kad ovako napises integracija se vrsi po

.
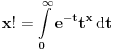
.
[ Bojan Basic @ 26.08.2008. 12:38 ] @
Naravno.
Ispravio sam, lapsus je bio u pitanju. Zahvaljujem.
[ igorpet @ 26.08.2008. 14:48 ] @
Citat:
Bojan Basic:
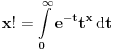
(Poslednji integral obeležava se sa
, što ima svoje razloge.)
Dakle,
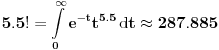
. Ista formula koristi se i za kompleksne vrednosti.
Hvala na informaciji.
Pogledao sam i dodatno na
http://en.wikipedia.org/wiki/Gamma_function
Nisam se bavio Gama funkcijom, nisam imao potrebe, ali deluje interasantno.
Malo sam skrenuo temu u drugom pravcu, ali nije namerno, ne zamerite (vise je bila stvar u neznanju).
[ petarm @ 26.08.2008. 15:07 ] @
Mislim da je ova tema vrlo korisno i zato sto pokazuje da nije korisno u nekoj matematickoj relaciji staviti
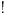
kad hoce neko nesto da naglasi.

Recimo neko bi mogao da napise veoma vazna relacija u matematici je

- tacno
jer povezuje brojeve koji se najcesce pominju u matematici i da joj skroz promeni znacenje napisavsi
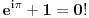
- netacno
[ igorpet @ 26.08.2008. 15:21 ] @
Citat:
petarm:
Recimo neko bi mogao da napise veoma vazna relacija u matematici je

- tacno
jer povezuje brojeve koji se najcesce pominju u matematici i da joj skroz promeni znacenje napisavsi
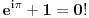
- netacno
Nazovimo to lingvisticko-matematickim paradoksom

Ili preciznije gramaticko-matematickim paradoksom


I najpravilnije bi bilo kad hocemo nesto u matematici da naglasimo da stavimo:

- uuu jeeee**te (al su ih povezali)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.