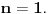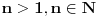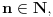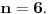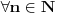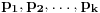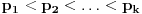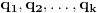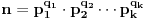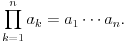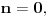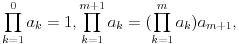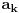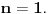Da li je takmičar tačno odgovorio?

Normalno da jeste, uz malu pomoć voditelja

Teško da je 1 prost broj. Onda ne bi važila osnovna teorema aritmetike po kojoj svaki prirodan broj ima jedinstvenu faktorizaciju preko prostih brojeva do na redosled činilaca. Na primer,

6 = 1*2*3 = 2*3.

Pritom je jedinica kao neutral za množenje proizvod nula prostih brojeva (prazan proizvod). U proste elemente se ne ubrajaju oni koji imaju u posmatranoj strukturi inverz u odnosu na množenje.

Bas tako. Evo vise detalja:
http://odin.mdacc.tmc.edu/~krc/numbers/fta.html

Pisem cisto povodom pomenute osnovne teoreme aritmetike.
Naime, iz nje ne sledi da broj 1 nije prost, jer ona vazi za sve
brojeve .

Sto se tice broja 1, on nije prost po definiciji.

Da li ti je 6 dovoljno veće od 1? Pogledaj prethodni primer. Kada bi 1 bio prost broj imali bismo jednu faktorizaciju broja 6 dužine dva i jednu dužine tri. Inače, osnovna teorema aritmetike važi za sve što ovde nije ni bitno jer je primenjena za

Cekaj malo prijatelju Nedeljko. :)

1. gde si ti video da se tvrdjenjem dokazuje ili negira definicija?
(povodom toga da iz osnovne teoreme aritmetike sledi da broj 1 nije prost)

2. sto se tice razloga koji navodim (jer ona vazi n>1 ...) on se odnosi na post
AMomcila koji sadrzajem na linku koji je naveo potvrdjuje tvoju recenicu. Bez
obzira na to sto je istorijski gledano broj 1 prvo bio prost a kasnije postao ni prost ni slozen, da bi se mogla dokazati osnovna teorema aritmetike u danasnjem
obliku, definicija je ipak, a i uvek ce biti "starija" od tvrdjenja.

i na kraju
3. ako pomenuta teorema vazi , koji su to jedinstveni
prosti brojevi takvi da je
i jedinstveni prirodni brojevi
tako da vazi ako stavimo n=1?

Prvo bih da primetim da je iz naših prethodnih postova jasno da se obojica slažemo oko toga da 1 nije prost broj, samo da to obrazlažemo na različite načine.

Drugo, nije sporno da je definicija starija od teoreme. Smisao mojih prethodnih postova je sledeći: Ako bismo koristili definiciju pojma prostog broja po kojoj je 1 prost broj, onda ne bi važila osnovna teorema aritmetike u formulaciji u kojoj se obično navodi zbog toga što bismo na primer broj 6 mogli da rastavimo na više načina. Stoga se ta teorema odnosi na definiciju pojma prostog broja po kojoj 1 nije prost broj.

Treće, neka je konačan niz od brojeva,. Tada se njegov proizvod definiše kao


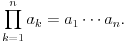
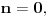
Ovde me nemoj držati za reč. Desna strana je samo oznaka za levu. No, suština ovoga je šta ako je tu odnosno ako je dati niz prazan (nema nijedan član)? Tada se uzima po dogovoru da je proizvod praznog niza neutral za množenje, odnosno 1.

A sad preciznije. Definicija proizvoda konačnog niza nije ono što gore piše već

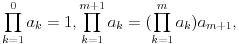
gde se podrazumeva da su svi za vrednosti koje odgovaraju granicama proizvoda definisani. Prostim jezikom rečeno, proizvod "ničega" je 1. Takav proizvod se još zove praznim proizvodom.

Odgovor na tvoje treće pitanje je: Broj 1 je proizvod praznog niza prostih brojeva. To sam napisao u jednom od prethodnih postova. Dakle, uz ovu konvenciju osnovna teorema aritmetike važi i za

Naravno da 1 nije prost po definiciji:

Prostim brojevima nazivaju se brojevi iz skupa prirodnih brojeva razliciti od jedinice koji osim jedinice i samog sebe nemaju drugih dijelilaca u skupu prirodnih brojeva.

Po kojoj formoli se određuje prost broj?
Kako mogu saznati da li je neki broj koji je veći od 7919 prost ?

http://sr.wikipedia.org/sr-ec/...%D0%BE%D1%98%D0%B5%D0%B2%D0%B0

Na ovoj adresi ima samo prvih 1000

Pa, deliš ga sa prostim brojevima ne većim od korena iz tog broja. Evo programa:

Da li to znači da ne postoji univerzalna KRAĆA formula za proveru prostog broja.
Može li se nekako skratiti postupak ovo je previše komplikovano.

Kako odrediti sve proste brojeve koji nisu veći od n?

Prvo napišeš sve brojeve od 2 do n. Onda zaokružiš broj 2 i precrtaš sve ostale brojeve koji su deljivi njime.
Prvi neprecrtani i nezaokruženi broj je 3. Zaokružiš njega i precrtaš sve ostale brojeve koji su deljivi njime.
Prvi neprecrtani i nezaokruženi broj je 5. Zaokružiš njega i precrtaš sve ostale brojeve koji su deljivi njime.

Postupak nastavljaš sve dok ima neprecrtanih i nezaokruženih brojeva. Kada ih više ne bude bilo, zaokruženi su prosti, a precrtani složeni. Ovaj postupak se zove Eratostenovo sito.

Ako te zanima za neki konkretan broj da li je prost ili složen, a veći je od 1, onda treba da proveriš da li je deljiv sa nekim prostim brojem koji nije veći od njegovog kvadratnog korena. Dakle, prvo mu odrediš kvadratni koren zanemarujući decimale. Onda prethodnim postupkom odrediš sve proste brojeve koji nisu veći od korena tog broja, pa onda proveri deljivost tog broja sa tim prostim brojevima. Ako je deljiv sa nekim, onda je složen, a inače prost.

Primer: Proverimo da li je broj 101 prost.

Koren iz 101 je između 10 i 11. Odredimo sve proste brojeve koji nisu veći od 10. Najpre napišimo sve brojeve od 2 do 10.

2,3,4,5,6,7,8,9,10

Prvi us pisku je prost. To je broj 2. Izbacimo sve deljivo sa njime.Ostaju brojevi

3,5,7,9

Prvi od ovih brojeva je prost. To je 3. Izbacimo sve deljivo njime.

5,7

Prvi od ovih brojeva je prost. To je 5. Izbacimo sve deljivo njime.

7

Prvi od ovih brojeva je 7 i on je prost. Izbacimo sve deljivo njime i ne ostaje nam ništa.

Dakle, prosti brojevi koji nisu veći od 10 su 2,3,5 i 7. Proverimo deljivost broja 101 sa svakim od njih. Ispostavlja se da nije deljiv ni sa jednim, pa je prost.

Zašto 1 nije prost broj:
http://www.youtube.com/watch?v=IQofiPqhJ_s

@jovan77
Postoje i kraći algoritmi, ali su podjednako komplikovani
Da je lako raditi sa prostim brojevima morali bi izmisliti neki novi način za kriptovanje podataka:

još malo Numberphile-a:
http://www.youtube.com/watch?v=M7kEpw1tn50

Odavno su smišljeni načini koji se ne zasnivaju na prostim brojevima i koji su otporni i na napade kvantnim računarima. Za više informacija pogledaj postkvantnu kriptografiju.

Broj 1 nije ni prost ni složen po definiciji prostih i složenih brojeva. Zašto su definicije tako izabrane? Pa, da bi se prostije formulisale teoreme koje ih koriste.