[ kUdtiHaEX @ 24.05.2004. 10:10 ] @
| Ovo je glupo pitanje, znam, ali ne mogu nikako da nateram da se moje matrice pomnoze. Moram da izvrsim mnozenje matrica uz proveru da li se one mogu pomnoziti. |
|
[ kUdtiHaEX @ 24.05.2004. 10:10 ] @
[ filmil @ 24.05.2004. 10:20 ] @
A koje je pitanje u pitanju?
Gde je sors? Vidovita Zorka je još uvek na odmoru, pa bi valjalo da nam daš malo materijala za razmišljanje. f [ Ivan Dimkovic @ 24.05.2004. 10:23 ] @
Ne mnoze se nikako :)
Cist C ne definise matrice kao tip, pa samim tim ni operacije nad matricama :) Ono sto mozes da uradis je: 1. Da sam implementiras matricnu algebru 2. Da koristis neku od javno dostupnih implementacija Ja sam odmah nasao nesto za C++ http://sourceforge.net/projects/ematrix/ A siguran sam da ima i za C, potrazi www.sourceforge.net [ igac @ 24.05.2004. 14:03 ] @
ili... uzmes linearnu algebru knjigu, procitas kako se mnoze matrice... ;))
prvo provjeris je a[ ]mxn i b[ ]nxp tj da je broj vrsta matrice a == broju kolona matrice b, pa onda mnozis po pravilu i stavljas sve u trecu matricu :] [ mojsilo2003 @ 24.05.2004. 23:54 ] @
Cao! Probaj sledece:
Code: #define maxdim 10 typedef float TRealMatrica[maxdim][maxdim]; . . . TRealMatrica A,B; . . . void ProizvodMatrica(float (*A)[maxdim],float (*B)[maxdim],int NA,int NB) { TRealMatrica P; int i,j,k; clrscr(); if(NA != NB) { printf("\nGRESKA: Redovi moraju biti isti!"); } else { for(i=0;i<NA;i++) for(j=0;j<NA;j++) { P[i][j]=0; for(k=0;k<NA;k++) P[i][j]=P[i][j]+A[i][k]*B[k][j]; } } ovo je algoritam za mnozenje kvadratnih matrica istih dimenzija pa ako pomaze... [ srki @ 25.05.2004. 00:25 ] @
A postoje i brzi algoritmi koji ti daju kompleksnost bolju od O(n^3).
[ caboom @ 25.05.2004. 02:09 ] @
koliko se secam, to jos uvek nije zatvoreno poglavlje algebre. secam se povrsno strassen-ovih i laderman-ovih algoritama, ali se ne secam da je neko stavio tacku na slucaj optimizacija kod proizvoljnog n*m matricnog mnozenja, ili gresim?
[ NetworkAdmin @ 25.05.2004. 07:29 ] @
[ filmil @ 25.05.2004. 08:11 ] @
Gilbert Strang u svojoj (doduše vremešnoj) knjizi „Linearna algebra i primene“ govori o algoritmima koji su blizu 2.5 u eksponentu i primećuje da je najverovatnija donja granica 2 „pošto nijedan broj između sadašnje granice i 2 ne izgleda naročito posebno“. Takođe kaže da dotični algoritmi uglavnom nisu zanimljivi za svakodnevnu upotrebu. Zanimljiviji su algoritmi koji rade na matricama poznate strukture.
f [ srki @ 25.05.2004. 08:37 ] @
Da, trenutno najbolji algoritam ima vreme izvrsavanja O(n2.376). Pronadjen je 1990. godine.
Ali problem je sto izgleda da je klasican algoritam brzi jer ovde su obracali paznju samo na broj mnozenja (kao "teze" operacije od sabiranja) ali kada se radi sa float brojevima onda je mnozenje brze od sabiranja koliko mi je poznato jer se mnozenje float brojeva radi tako sto se posebno pomnoze mantise i posebno saberu eksponenti. [Ovu poruku je menjao srki dana 26.05.2004. u 01:25 GMT] [ NetworkAdmin @ 25.05.2004. 11:01 ] @
interesantne su razne iterativne metode za rjesavanje dijagonalno dominantnih matrica koje imaju samo odredjeni broj non-null dijagonala. ali ovo je specijalni slucaj... doduse taj specijalni slucaj je primjenljiv na mnogim fizickim problemima kao recimo proracun toka fluida metodom konacnih volumena :)
[ kUdtiHaEX @ 25.05.2004. 13:54 ] @
Hvala na odgovorima, inace radio sam sledece:
Code: #include <stdio.h> #include <stdlib.h> main() { int k,p,i,j,m,n,*a,*b,*c; printf("Mnozenje matrica se vrsi ako je broj kolona jedne matrice\njednak broju vrste druge matrice\n"); printf("Unesite dimenzije prve matrice:\n"); scanf("%d%d",&m,&n); printf("Unesite dimenzije druge matrice:\n"); scanf("%d%d",&k,&p); while (m>0 && n>0 && n==k){ a=(int*)malloc(m*n*sizeof(int)); if (a==NULL) break; b=(int*)malloc(n*p*sizeof(int)); if (b==NULL) break; printf("Unesite elemente prve matrice:\n"); for (i=0;i<m;i++) for (j=0;j<n;j++) scanf("%d",&a[i*n+j]); printf("Uneta matrica je:\n"); for (i=0;i<m;i++){ for (j=0;j<n;j++) printf("%d ",a[i*n+j]); putchar('\n'); } printf("Unesite elemente druge matrice:\n"); for (i=0;i<n;i++) for (j=0;j<p;j++) scanf("%d",&b[i*p+j]); printf("Uneta matrica je:\n"); for (i=0;i<n;i++){ for (j=0;j<p;j++) printf("%d ",b[i*p+j]); putchar('\n'); } c=(int*)malloc(m*p*sizeof(int)); if (c==NULL) break; for (i=0;i<m;i++) for (j=0;j<n;j++) for (k=0;k<p;k++) c[k*p+i]=a[n*j+i]*b[p*k+j]; printf("Proizvod matrica je:\n"); for (i=0;i<m;i++){ for (j=0;j<p;j++) printf("%d ",c[i*p+j]); putchar('\n'); } printf("\n\n"); free(a); free(b); free(c); printf("Mnozenje matrica se vrsi ako je broj kolona jedne matrice\njednak broju vrste druge matrice\n"); printf("Unesite dimenzije prve matrice:\n"); scanf("%d%d",&m,&n); printf("Unesite dimenzije druge matrice:\n"); scanf("%d%d",&k,&p); } } Ovaj algoritam za mnozenje matrica nije tacan ( u smislu dobijanja pogresnog rezultata, jer sam bio izmesao vrste i kolone matrica ali sam to ispravio, ispravljeni kod mi nije pri ruci sada). [ medi @ 28.05.2004. 09:36 ] @
Pogriješio si ovdje:
for (i=0;i<m;i++) for (j=0;j<n;j++) for (k=0;k<p;k++) c[k*p+i]=a[n*j+i]*b[p*k+j]; ali dobro to, nek neko da ideju za stepenovanje matrica !? Jel samo množenje uzastopno ili postoji neki još jednostavniji način !? [ filmil @ 28.05.2004. 09:46 ] @
Postoji više jednostavnijih načina za stepenovanje. Jedan bi bio recimo korišćenje dinamičkog programiranja gde se pamte međurezultati A, A2, A4, što se može svesti na pamćenje samo jednog međurezultata pa se stepenovanje sa n može obaviti u
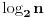 koraka. koraka. Druga mogućnost bi bila korišćenje Kejli-Hamiltonove teoreme, mada je to verovatno korisno samo za matrice poznate strukture. Sigurno postoji još neki štos. f [ medi @ 28.05.2004. 18:54 ] @
Sviđa mi se ovo sa pamćenjem međurezltata, pokušaću uraditi na taj način. Ako neko ima još neku ideju za brže i jednostavnije stepenovanje matrica neka javi!
Hvala! Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|