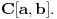Pojam uniformne ograničene ograničenosti se vezuje isključivo za familije funkcija, odnosno operatora, odnosno nizova, a nikako za jednu funkciju, odnosno niz, odnosno operator.

Jel može precizna definicija?
Prenosim čitavu teoremu i dio dokaza gdje se spominje uniformna ograničenost:



OSim toga nije mi u ovom dijelu jasno kako dokazuje (7) indukcijom po k kada u (7) se uopšte ne spominje k.

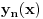
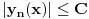
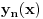
Da, ovde se govori o uniformno ograničenom nizu funkcija . To znači da postoji konstanta takva da je za sve prirodne brojeve i sve iz domena funkcija . Ako se ne kaže na kom je skupu taj niz funkcija uniformno ogranichen (kada moraju sve funkcije iz niza definisane na tom skupu), onda se podrazumeva da su domeni svih funkcija iz tog niza funkcija biti jednaki.

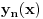
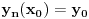
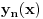
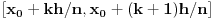
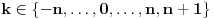
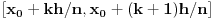
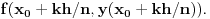
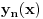
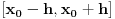
Drugo, niz funkcija ti za ovu namenu i nije baš nabolje definisan.Trebalo bi da bude i da funkcija bude neprekidna i linearna na svakom od degmanata za i tako da koeficijent pravca na odsečku bude jednak Nije teško pokazati da za svaki prirodan broj postoji jedinstvena funkcija definisana na intervalu koja ispunjava tražene uslove.

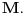
No, pošto koeficijent pravca na bilo kom od segmenata ne može preći po apsolutnoj vrednosti, pa stoga važi tražena nejednakost (7). Iz istog razloga su funkcije iz tog niza funkcija ravnomerno neprekidne. Lipšicove su sa istom konstantom Sada možeš da primeniš Arcela-Askolijevu teoremu o relativnoj kompaktnosti Banahovog prostora

Nije mi jasno kako definišeš kojeficijent pravca koef= pomoću y kada y nije definisana funkcija?

Da se taj dokaz kojeg navodiš naziva kao dokaz pomoću Eulerovih poligonalnih linija,pošto u knjizi koju ja čitam navodi se da je dokaz od Tonellija.
Dalje,ne znam ni šta znači "ravnomjerno neprekidne"?
Položio sam Analizu1 ,Analizu2 i Kompleksnu analizu i nigdje nismo to učili.

Također ni teoremu Arcela-Askolija.Da li mi to imamo nedoslednost u nastavi?

Prvo, . Sada znamo da je za a samim tim i da je . Odatle dalje zaklučujemo da na segmentu važi za . Postupak se dalje slično produžava. Na drugu starnu ide simertično. Dakle, za će koeficijent pravca funkcije na odsečku zapravo biti , tako da imam tu grešku u prethodnom postu. Za Tonelijev dokaz ne znam, ali formule su ti očigledno bagirane. Familija funkcija je ravnomrno neprekidna na nekom skupu ako za svako postoji tako da za ma koje x,y iz tog skupa i ma koju funkciju f iz te familije važi da ako su x i y na rastojanju manjem od , onda su i f(x) i f(y) na rstojanju manjem od

Teorema Arcela Askolija tvrdi da ako je F familija ravnomerno ograničenih i ravnomerno neprekidnihrealnih funkcija sa domenom [a,b] za a<b, onda se iz svakog niza funkcija iz te familije može izdvojiti ravnomerno konvergentan podniz. Niz funkcija sa istim domenom ravnomerno konvergira ka funkciji sa tim domenom ako za svako postoji prirodan broj N takav da za sve n>N i svako x iz domena važi da su i na manjem rastojanju od

Da sumiramo definicije (da li sam ih dobro shvatio?):

1.Familija funkcija može biti uniformno neprekidna(ravnomjerno neprekidna) što je različito od situacije kada je svaka funkcija familije uniformno neprekidna.
2.Familija funkcija može biti uniformno ograničena što je različito od situacije kada je svaka funkcija familije ograničena.Jedna funkcija ne može biti uniformno ograničena.
3.Niz funkcija uniformno konvergira ka f(x) što je različito kada za svako iz domena niz konvergira ka (tačkasta konvergencija)

U definisanju koeficijenta pravca f-je na odsječku zar ne bi trebalo biti umjesto jer ako uzmemo drugi slučaj za k=0 dobijemo da na intervalu je koeficijent pravca što nije tako zar ne (trebao bi biti ?

I kako iz uslova da su koeficijenti manji od M izvodiš uslove potrebne za primjenu teoreme Arcela Askolija?

Da, dobro si razumeo definicije. A ovo što te buni oko koeficijenta pravca važi samo za k<0. Ne možeš to primenjivati na slučaj kada je k=0. Za k>=0 važi formula koju si napisao.

Pa, ako su svi koeficijenti pravaca po apsolutnoj vrednosti manji do jednaki od M, onda su sve te funkcije Lipšicove sa Lipšicovom konstantom M, odakle je ta familija funkcija ravnomerno neprekidna. No, domen funkcija iz te familije je ograničen i ima širinu 2h, pri čemu se središnja tačka pri svim tim funkcijama slika u isti tačku, pa su sve te funkcije po apsolutnoj vrednosti ograničene sa

Valja li dokaz da je


Neka su komadići linearnih f-ja od kojih pravimo zadati sa
za
Tada za proizvoljno x postoji k tako da
(1)
Ali
pa je (1) dalje jednako

Ali
i slično nastavljajući da razlažemo prvi sabirak dobijamo da je (1) jednako







Ravnomjernu neprekidnost još nisam izveo trenutno nemam ideju.

A kada primjenimo teoremu Arzela Ascolija i dobijemo funkciju y(x) kako se dalje dokazuje da je ona rešenje?

Dovoljno je koristiti Lipšicovu konstantu i za uniformnu ograničenost i za uniformnu neprekidnost. Sve je detaljno uradjeno u sjajnoj knjizi Slobodana Aljančića "Uvod u Relnu i Funkcionalnu Analizu".