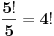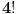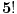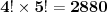Pošto niko do sada nije rešio nijedan zadatak postujem rešenje 4. zadatka:

Neka je A skup onih brojeva manjih od milion kod kojih je zbri cifara 44 a skup B onih kod kojih je zbir 10. Neka:
f: A -> B i
f(a)=999999-a
Na primer neka je a=123004, f(a)=876995 tj pripada skupu B. Lako vidi da je f bijekcija tj. |A|=|B|, tj brojeva kod kojih je zbir cifara 44 ima isto onoliko koliko i onih kod kojih je zbir cifara 10.

poz.

PS. nadam se da će neko rešiti bar jedan od preostala 3 zadatka.

lako se vidi,ali je ipak potrebno dokazati
samo sugerisem


iskoristicu priliku da kazem da je ovo tip 'namestenog' zadatka,sto ne znaci da se ne moze resiti sopstvenim dolazenjem do resenja,ali je potrebno malo matematickog iskustva da bi se to postiglo.



kajla,predlozicu ti da kad ti postavis neki zadatak ipak sacekas nesto vise od 5-6 dana sa resenjima,jer mozda neko dolazi jednom nedeljno i nema priliku da pokusa da uradi zadatak,a da ne vidi i resenje.
ili prosto nema vremena da odmah radi tvoje zadatke.
hvala

Čini mi se da su ovi zadaci više od nedelju dana na forumu.

poz.

pa,tvoj izbor,ja sam samo predlozila
tnx

Na brzinu sam dobio da je broj ovih brojeva 51. Ako je rezultat tacan poslacu resenje.

Pravo da ti kažem više se ni sam nesećam...morao bih ponovo da rešavam zadatak da bi video...uglavnom postuj rešenje pa ćemo da vidimo dali je tačno ili ne. Ako nije onda ćemo da nađemo grešku...

poz.

Pre bih rekao da je ovo jedan LEP zadatak nego da je namešten...

poz.

--POSTO NEMAM PREVISE VREMENA SAMO CU SKICIRATI RESENJA PRVA TRI ZADATKA!!!
-Resenje prvog zadatka je 102 trocifrena broja!!!
Posto je apsolutna razlika dve susedne cifre deljiva sa 3 zakljucuje se da sve tri cifre moraju da budu oblika 3k,3k+1 ili 3k+2 ,pa je broj trocifrenih sa ciframa oblika 3k 3*4*4=48 ,oblika 3k+1 3*3*3=27 ,a oblika 3k+2 3*3*3=27.
UKUPNO 102!!!!!
-Resenje drugog zadatka je 22 broj!!!
Da ne objasnjavam resenje to su brojevi:
12,13,14,15,16,17,18,19,24,26,28,36,39,48,124,126,128,136,139,148,248,1248.
UKUPNO 22!!!!!!!
-Resesnje treceg zadatka je 40 trocifrena broja!!!
Ako su od tri cifre samo jedna cifra 0 ili 3 ostale dve cifre moraju da budu 1 i 5 ili 2 i 4 da bi trocifren broj bio deljiv sa 3. Ima 2*4=8 kombinacija (kad broj ima samo jednu 0 i nijednu 3) i 3*4=12 (kad broj ima samo jednu 3 i nijednu 0).
Znaci trocifrenih brojeva sa samo jednom 0 ili 3 kiji su deljivi sa 3 ima 20(**).
Dalje(da ne tupim previse) lako se dokazuje da u ostalim slucajevima trocifren broj je deljiv sa 3 ako su mu sve cifre oblika 3k,3k+1,3k+2.
Sve cifre oblika 3k(0 i 3) obrazuju 1*2*2=4 broja(**).
Sve cifre oblika 3k+1(1 i 4) ima 2*2*2=8 broja(**).
Sve cifre oblika 3k+2(2 i 5) ima 2*2*2=8 broja(**).
Sabiranjem svih (**) dobijamo:
UKUPNO 40!!!!!
--NADAM SE DA NEMA GRESAKA POSTO SAM SVA TRI URADIO NA BRZINU!!!!

jel moze meni neko da uradi zadatak????

za okruglim stolom ima 10 mesta....na koliko nacina mogu da se raporede 5 devojaka&5momaka tako da devojke ne sede jedna pored druge&momci ne sede jedni pored drugih....

pomagajte sto pre....sutra imam pismeni sa ovim zadatkom....

Aj prvo da poredjamo seke pa cemo onda bate.

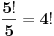
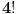
Ima nacina da poredjamo seke (zbog simetrije u rotaciji je , a ne ).

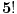
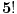
Sada redjamo bate. Posto ih redjamo u odnosu na seke ne postoji simetrija u rotaciji i postoji nacina da ih raspodelimo oko stola.

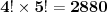
Dakle, ima mogucih nacina da 5 bata i 5 seka sedi za istim stolom tako da su ispunjeni uslovi zadatk.



Sada ti ovo verovatno nije potrebno jer ti je trebalo za pismeni, ali mozda ce nekom drugom zatrebati :)

ni ne znas kolko mi je pomglo.....pismeni mi pocinje za pola sata....hvala puno!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!