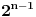
Možeš da napraviš binarno stablo sa elementima (brojevima) koje si dobio, rekurzivno isprobaš sve moguće putanje i da zbirove slažeš u niz koji ima elemenata (toliko ima putanja), gde je n broj vrsta. Onda nađeš najveći element niza.
Koliko vidim samo se najveći zbir i traži, ne i putanja.

Rešenje može dosta da se ubrza ako se vidi da od tih svih puteva mnogi imaju zajedničke parcijalne puteve. Ovo je verovatno jedan od osnovnih problema u kojima može da se iskoristi tzv. dinamičko programiranje.

Posmatramo n-ti red trougla, i neki broj u njemu (recimo dvojka u poslednjem redu).

Pitamo se: koji je najveći mogući zbir među svim putevima koji se završavaju u tom broju. Pošto tih zbirova očigledno ima mnogo, na prvi pogled je nejasno kako možemo sve da ih pregledamo i pronađemo najveći. Međutim, postoji jednostavan trik koji rešava stvar.

Sve putanje koje se završavaju u broju 2 moraju da prođu kroz brojeve koji su gore-levo, odn. gore-desno u šemi (to su 4 odn. 7). Pretpostavimo sada da znamo koji su maksimalni zbirovi svih puteva koji se završavaju u 4, odn. u 7. Ako to znamo onda znamo i sledeće: maksimalni zbir svih puteva koji se završavaju u 2 jednak je većem od zbirova puteva za 4 i 7, uvećanom za 2.

Dakle AKO znamo maksimalne zbirove za 4 i 7, možemo da „proizvedemo“ maksimalni zbir za 2 jednostavnom operacijom (maksimum plus vrednost broja). Ostaje nam još da nekako sračunamo zbirove za 4 i za 7. To se može učiniti na isti način, gledanjem maksimalnih zbirova koji su gore-levo, odn. gore-desno, računanje maksimuma itd.

Još treba da se primeti da je sve maksimume u jednom redu moguće sračunati ako su poznati maksimumi iz prethodnog reda. Sada je rešenje jednostavno: pre nego što sračunamo maksimum u jednom redu, sračunaćemo sve maksimume u prethodnom, a zatim na osnovu njih i maksimume u tekućem.
Zahvaljujući tome što u ranijim redovima ima manje brojeva, problem je jednostavniji. Najprostije je sračunati maksimum u prvom redu u kome stoji samo jedan broj.

Dakle algoritam je:

– za prvi red, maksimum je jednak prvom i jedinom broju.
– maksimumi za trenutni red se izračunaju na osnovu poznatih maksimuma za prethodni red i gore pomenute formule, novosračunati maksimumi se zapamte za sledeći prolazak kroz petlju.
– pomerimo se na sledeći red i ponovimo prethodno.
– kad izvrtimo petlju za sve redove, prođemo kroz poslednji izračunati niz maksimuma i nađemo koji je najveći element.

f

Dobre ideje, nema sta. Hvala na brzim odgovorima.