[ nervozna @ 07.02.2002. 22:58 ] @
neka je f(x)=x^x koliko je f'(x)? |
|
[ nervozna @ 07.02.2002. 22:58 ] @
[ lucky @ 08.02.2002. 22:54 ] @
Citat: nervozna: neka je f(x)=x^x koliko je f'(x)? Ovo je jednostavno! Moze li da se postuje resenje ? [ nervozna @ 08.02.2002. 23:14 ] @
PA NARAVNO DA MOZE
i jeste prilicno jednostavno [ lucky @ 09.02.2002. 14:38 ] @
Resenje: f(x) = x^x = e^ln(x^x) = e^(x*lnx) f '(x) = (e^(x*lnx)) ' = (e^(x*lnx))*(lnx + 1) Pozdrav [ Mikky @ 10.02.2002. 23:23 ] @
kada se koristi ta fora da se funkcija stavlja kao e^ln( f(x) )
tj ima li pravilo u kojim situacijama to upotrebljavati, kao npr ovo sad [ nervozna @ 10.02.2002. 23:52 ] @
Citat: lucky: Resenje: f(x) = x^x = e^ln(x^x) = e^(x*lnx) f '(x) = (e^(x*lnx)) ' = (e^(x*lnx))*(lnx + 1) Pozdrav samo da pojednostavim,tj da vratim na pocetak tvoje resenje f'(x)=(x^x)*(lnx+1) ova -fora- se koristi u situacijama kad neka uobicajena matematicka konstrukcija ne moze da se iskoristi nema nikakvih pravila [ Vojislav Milunovic @ 12.02.2002. 03:26 ] @
Citat: nervozna: neka je f(x)=x^x koliko je f'(x)? Ok ajde da ja dam jedno resenje: ln (f(x)) = lnx^x = x lnx f'(x)/f(x) = (1) * lnx + 1/x * x f'(x)/f(x) = lnx + 1 f'(x) = (1 + lnx)* f(x) f'(x) = x^x * (1 +lnx) A nije lose :) Eto primer kako bez koriscenja e u kompletnoj proceduri da se resi ovaj problem. ok ln je log sa osnovom e ali to sad zanemarimo jel nigde u postupku nisam pisao e :) [ random @ 12.02.2002. 14:22 ] @
Fali ti drugi korak,
(ln f(x))' = f'(x) * f(x)^(-1) = f'(x)/f(x) a treći (derivacija proizvoda) je višak (trivijalan). I za moj ukus nije elegantnije. P.S. Gojko kad ćeš da ubaciš MathMl i [math] kodove? ;o) P.P.S. Valjalo bi još dodati da je uslov za celu ovu priču da f(x) > 0 na celom domenu definisanosti. [ nervozna @ 12.02.2002. 22:50 ] @
resenje je ipak interesantno,jos i zato sto se ovakve konstrukcije koriste pri resavanju diferencijalnih jednacina
zadatak se moze jos komplikovanije resiti,kao ,recimo,pisanjem f-je u obliku f-je sa dve nepoznate f(x,y)=x^y,pa restrikcija te f-je na onom delu f-je gde je x=y daje resenje jos mislim da je suvisno reci da je ln log sa osnovom e,jer je dogovoreno da se log sa osnovom e oznacava sa ln poz [Ovu poruku je menjao Vojislav Milunovic dana 13.02.2002 u 08:57 PM GMT] [ random @ 13.02.2002. 01:06 ] @
Zapravo mislim da se sada logaritam x sa osnovom e oznacava kao log x (to je nekad bio dekadni, sa osnovom deset, ali sad dekadni više nije interesantan pošto su log. tablice izašle iz upotrebe sa sveprisutnošću računara). Ne znam šta kaže standard, ali u knigama sa ETF-a se prirodni logaritam obeležava sa log x, već preko nekoliko godina unazad, a znam da su oni dosta ažurni po pitanju standarda.
[ nervozna @ 13.02.2002. 01:22 ] @
prvi put cujem za tako nesto!
ja jos uvek studiram mat i jos uvek se u nasim knjigama koristi oznaka ln mislim da ce matematicari ostati pri tome,jer bi zaista bilo neprakticno menjati log se koristi za bilo koju drugu osnovu(ne samo za 10),koliko mene naucise ln se zove prirodni logaritam,kao takav je izdvojen od ostalih poz [Ovu poruku je menjao Vojislav Milunovic dana 13.02.2002 u 08:56 PM GMT] [ MoHicAn @ 13.02.2002. 02:07 ] @
Samo log x ti je logaritam od x za osnovu 10 ako ne napises mali index izmedju log i x koji ce oznacavati osnovu i to nije ja mislim nikakav prirodan logaritam itd itd vec je samo uzeto 10 ja mislim radi uproscavanja pisanja ...
[ nervozna @ 13.02.2002. 02:22 ] @
jos cu otici kod nekog svog profesora da ga pitam da nisu poslednjih dana uvedena nova pravila!
ja kazem sta se kod mene uci na faxu mi,recimo,koristimo log x bez pisanja osnove kad mislimo na osnovu 2(to rade programeri na mom faxu) a ln,kao prirodni logaritam se u definiciji tako oznacava i zove ja sam tako ucila PRIGOVOR MODERATORA Zasto svaki put kad pises odgovor moras da quotujes celu poruku. To uopste lepo ne izgleda. [Ovu poruku je menjao Vojislav Milunovic dana 13.02.2002 u 08:59 PM GMT] [ filmil @ 13.02.2002. 16:41 ] @
Citat: nervozna: Citat: random: Zapravo mislim da se sada logaritam x sa osnovom e oznacava kao log x računara). Ne znam šta kaže standard, ali u knigama sa ETF-a se prirodni logaritam obeležava sa log x, već preko nekoliko godina unazad, a znam da su oni dosta ažurni po pitanju standarda. prvi put cujem za tako nesto! ... ln se zove prirodni logaritam,kao takav je izdvojen od ostalih poz Sto se ETF tice, objasnjenje je vrlo jednostavno. Verujem da se misli na knjigu Matematicka analiza od M. Merklea. Oznake u anglosaksonskoj literaturi za neke funkcije drugacije su od oznaka u nasoj i po defaultu na raspolaganju u programu LaTeX, u kome se za stampu priprema vecina matematickih knjiga. LaTeX definise funkciju log ali ne i ln (logaritam 'naturalis'?), pa su autori odlucili da se malo posvadjaju sa starim konvencijama. Eto sta ucini prljavi Zapad. Druga mogucnost: u C-u na primer, postoje funkcije log i log10 koje daju redom prirodni i logaritam sa osnovom 10. Sad valjda, pitanje je ko smatra koja je konvencija 'starija'. Mislim da nije lose da se svaki put naglasi o cemu se misli. poz. [ Vojislav Milunovic @ 13.02.2002. 21:00 ] @
Sta znam ovde u USA za log X se misli na osnovu 10, a za ln X za osnovu e.
[ nervozna @ 13.02.2002. 23:54 ] @
sto se mene tice,svejedno mi je kako ce se sta oznacavati,samo da je to unapred dogovoreno
rekla bih da se ovde ipak radi o razlicitim standardima,i to ne samo kako ih koja zamlja utvrdi,vec fakultet ln se kao oznaka nije koristio ni za jednu drugu osnovu,osim za osnovu e i mislim da to nije sporno za koristenje log x ipak treba reci o kojoj se osnovi radi,bas zbog razlicitih standarda poz [Ovu poruku je menjao nervozna dana 14.02.2002 u 02:42 AM GMT] [ random @ 14.02.2002. 01:37 ] @
Citat: filmil: Sto se ETF tice, objasnjenje je vrlo jednostavno. Verujem da se misli na knjigu Matematicka analiza od M. Merklea. Takođe i Matematika III, a verujem i IV. Sa druge strane, zar i profesori na PMF-u ne pišu svoje radove u TeX-u? Konačno, u mnogim situacijama je zapravo nebitno koja je osnova logaritma (kao u Vojinom primeru), ali složiću se da je ln uvek nedvosmisleno jasna oznaka. Koliko sam sad iskopao po netu, čest je običaj da matematičari obeležavaju ln x kao log x. Zatim ispada da Rusi imaju neku svoju notaciju -- obeležavaju logaritam sa osnovom 10 kao lg x, a Ameri često koriste lg kao oznaku za binarni logaritam. Da parafraziram čestu uzrečicu u OpenSource zajednici: ko kaže da nema standarda? Ima ih ne jedan nego koliko hoćeš... [ filmil @ 14.02.2002. 08:20 ] @
Citat: random: Takođe i Matematika III, a verujem i IV. Sa druge strane, zar i profesori na PMF-u ne pišu svoje radove u TeX-u? Ne bih znao za to, al' sam se navikao (davno to bese :) pa mi vise ne bode oci. poz. [ Vojislav Milunovic @ 16.02.2002. 17:40 ] @
Citat: Mikky: kada se koristi ta fora da se funkcija stavlja kao e^ln( f(x) ) tj ima li pravilo u kojim situacijama to upotrebljavati, kao npr ovo sad To da se funkcija stavi na lnf(x) se koristi najcesce kad u eksponentu imas promenljivu. Recimo 1^x i slicno. Recimo imas 1^x i uradis vako ln f(x) = ln (1^x) = x ln1 f'(x)/f(x) = ln1 (ln1 je konstanta) f'(x) = ln1 * f(x) f'(x) = ln1 * 1^x i eto ti primer kada da koristis lna = lnb [ filmil @ 17.02.2002. 11:29 ] @
Citat: Vojislav Milunovic: Citat: Mikky: kada se koristi ta fora da se funkcija stavlja kao e^ln( f(x) ) tj ima li pravilo u kojim situacijama to upotrebljavati, kao npr ovo sad To da se funkcija stavi na lnf(x) se koristi najcesce kad u eksponentu imas promenljivu. Recimo 1^x i slicno. U stvari, implicitno se koristi svaki put. To je zato sto se stepenovanje $ a^b $ definise preko $e^x$, koje se eksplicitno moze sracunati kao poznati red: $ \sum_k x^k/k! $. $\ln x$ se onda definise kao inverzna funkcija od $ e^x$, pa zatim: $$ a^b \equiv e^{b \ln a } $. jer uobicajena srednjoskolska "definicija" (koja mi nikada nije bila jasna): $ a^b = a \dot a \cdots $ prosto nema smisla kada je $b$ ne-ceo broj. Kako $\sqrt 2$ puta pomnoziti $a$ sa samim sobom? To se cesto zaboravlja. poz. [ anon315 @ 02.01.2003. 06:48 ] @
[ darkosos @ 04.01.2003. 08:53 ] @
Dodao bih samo da se fora koristi za sve f(x)^g(x). Razlog zbog koga mora biti f(x)>0 nije u kasnijem logaritmovanju, vec sto u R nije definisano stepenovanje negativnog broja proizvoljnim realnim ( (-1)^(1/2) "=" i ).
Sto se tice oznaka za prirodni logaritam, ja sam na mat. fak. naucio da ga pisem kao log. Dakle i tamo zavisi kod kog profesora slusas, odnosno sta je on cit'o kad je bio mali. [ petarm @ 13.03.2010. 20:55 ] @
Citat: Vojislav Milunovic: Sta znam ovde u USA za log X se misli na osnovu 10, a za ln X za osnovu e. Citat: nervozna: sto se mene tice,svejedno mi je kako ce se sta oznacavati,samo da je to unapred dogovoreno rekla bih da se ovde ipak radi o razlicitim standardima,i to ne samo kako ih koja zamlja utvrdi,vec fakultet ln se kao oznaka nije koristio ni za jednu drugu osnovu,osim za osnovu e i mislim da to nije sporno za koristenje log x ipak treba reci o kojoj se osnovi radi,bas zbog razlicitih standarda poz [Ovu poruku je menjao nervozna dana 14.02.2002 u 02:42 AM GMT] U većini knjiga koje sam ja koristio je oznaka 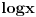 bila predviđena za dekadni logaritam. Mada naglasio bih u vezi sa ovom temom da se u zbirci za 2. razred gimnazije koristila oznaka bila predviđena za dekadni logaritam. Mada naglasio bih u vezi sa ovom temom da se u zbirci za 2. razred gimnazije koristila oznaka 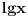 . Što samo pokazuje kolko nijednu oznaku nije nužno koristiti i da autor mora naglasiti šta pod tim misli ukoliko ne koristi da je to dekadni logaritam. Naleteo sam na nekoliko knjiga gde se pod . Što samo pokazuje kolko nijednu oznaku nije nužno koristiti i da autor mora naglasiti šta pod tim misli ukoliko ne koristi da je to dekadni logaritam. Naleteo sam na nekoliko knjiga gde se pod 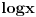 podrazumevamo prirodni logaritam, ali je to bilo i naglašeno. podrazumevamo prirodni logaritam, ali je to bilo i naglašeno. [ Cabo @ 14.03.2010. 17:05 ] @
[ petarm @ 14.03.2010. 19:11 ] @
Samo da se vratim i na temu sa početka:
Ako je  koliko je 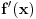 ? ?Ovo se može raditi i kao izvod implicitno zadate funkcije.  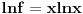 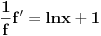  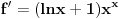 Citat: Tako sam i ja učio u gimaziji ali dobro se sećam da, iako smo tako radili na časovima, u zbirci koju su pisali Ognjanović i Ivanović, ako se ne varam, je dekadni logaritam bio označen sa  . Ali to je već sad pitanje oznaka. Neko sinus hiperbolični označava sa . Ali to je već sad pitanje oznaka. Neko sinus hiperbolični označava sa 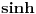 , a neko sa , a neko sa 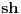 , ,[ petarm @ 14.03.2010. 23:36 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|