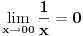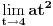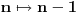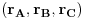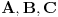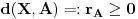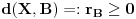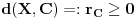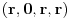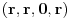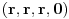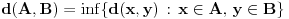[ anon315 @ 21.02.2002. 12:47 ] @
| Pretpostavimo idealan slucaj - tj. da se sledeci uslovi mogu ostvariti sa greskom = 0 Imamo Peru i Miku | Pera u tacki A, Mika u tacki B. Rastojanje tacaka A i B je TACNO 1m. Mika predje TACNO jednu polovinu puta, sada je rastojanje TACNO 0.5 Mika opet predje TACNO jednu polovinu puta, sada je rastojanje 0.25 I tako beskonacno puta Naime, koliko god puta budemo delili rastojanje sa dva ono NIKAD nece biti jednako 0, vec priblizno 0. Po toj logici Mika teorijski nikad nece stici tj. pipnuti Peru, a prakticno naravno hoce Naime, postavlja se pitanje kako ja mogu tebe da pipnem ako je to teorisjki vrlo jasno nemoguce ?! Sta mislite o ovom razmisljanju ? Necu se zadovoljiti odgovorom preko limesa (granicnih vrednosti) i pricom da nakon beskonacno deljenja mozemo smatrati to malo rastojanje nulom i kraj price, znaci aproksimacijom ... poz. |