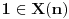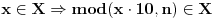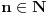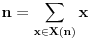|
|
[ Vojin Petrovic @ 04.09.2004. 22:08 ] @
|
| Svojevremeno sam pokusavao da nadjem u literaturi uslov deljivosti brojem 7, ali bezuspesno, navodno suvise je komplikovano za objasniti, pa sam odavno seo i provali kako se racuna uslov. Hteo bih da cujem ako jos neko zna kako ide uslov deljivosti, mozda sam otkrio nesto novo, a mozda sam otkrio nesto sto se vec dugo zna. Da ne bi ispalo da se foliram da imam resenje nego da cekam da mi neko kaze, samo cu reci da je broj 3 jako bitan broj u tome.
Pozdrav |
[ neor @ 05.09.2004. 07:34 ] @
Za svaki broj se moze naci pravilo kojim se na osnovu cifara oredjuje deljivost.
Na primer za broj P, proizvoljan broj A zapisan u osnovi B je
A = an...a2a1a0
A ce biti deljivo sa P ako je zbir
a0 * (B0 mod P) + a1 * (B1 mod P) + ... an * (Bn mod P)
deljiv sa P.
Znaci za 7 koeficijenti (Bi mod P) su 1,3,2,6,4,5 i dalje se ponavlja ovih 6.
Ovo se moze malo pojednostaviti jer se umesto 6,4,5 mogu uzeti -1,-3,-2.
[ Vojin Petrovic @ 05.09.2004. 12:59 ] @
vidis, neor, to nisam znao... ipak sam ja samo glupi hemicar 
no nasao sam nesto drugo...
broj A, kako ga ti lepo predstavljas a n...a 2a 1a 0 je deljiv sa 7 takodje ako je zbir a 0*3 0 + a 1*3 1 + a 2*3 2 + ...... + a n*3 n deljivo sa 7... ne znam zasto al funkcionise [ neor @ 05.09.2004. 13:29 ] @
To je zato sto 3 i 10 imaju isti ostatak pri deljenju sa 7 pa onda to vazi i za sve njihove stepene.
[ darkosos @ 06.09.2004. 07:14 ] @
Citat: Znaci za 7 koeficijenti (Bi mod P) su 1,3,2,6,4,5 i dalje se ponavlja ovih 6.
Znači samo nađemo ostatke deljenja odgovarajućeg stepena desetke:
1 = 1 (mod 7)
10 = 3 (mod 7)
100 = 2 (mod 7)
1000 = 6 (mod 7)
10000 = 4 (mod 7)
100000 = 5 (mod 7)
?
Onda 7 nije baš neki broj s' kojim želiš da se kačiš :)
U stvari, ono prethodno može i ovako:
pošto je 10 '=' 3
1*3 = 3
3*3 = 9 '=' 2
2*3 = 6
6*3 = 18 '=' 4
4*3 = 12 '=' 5
5*3 = 15 '=' 1
i opet smo na početku.
Npr., 13 je umereniji: 1 10 4. [ Nedeljko @ 06.09.2004. 23:09 ] @
Ama ljudi, rešenje je u jednakostima koje je napisao darkosos. Ostatak pri delenju broja 71085319328 pri delenju sa 7 je isti kao ostatak pri delenju sa 7 broja
1*8+3*2+2*3+6*9+4*1+5*3+1*5+3*8+2*0+6*1+4*.7.
[ darkosos @ 09.09.2004. 16:15 ] @
Evo sad inspiracije i za zadatak:
Za prirodan broj n, označimo sa X(n) skup koji zadovoljava sledeće osobine:
1. 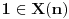
2. 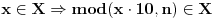
gde je mod(a,b) ostatak posle deljenja a sa b.
Odrediti sve 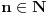 tdj. 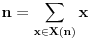 . [ neor @ 09.09.2004. 17:19 ] @
Za pocetak vazi za sve brojeve koji se pisu samo jedinicama (1,11,111,....)
Na zalost to nisu svi. Do 10000 zadovljavaju jos 37, 429, 2849, 3003, 4649 i 8547.
Ne znam kako njih da uklopim.
[ Specter_M @ 09.09.2004. 21:04 ] @
Postoji jedan nacin analogan onim standardnim za 3, 5, 9, 11, itd. ali nije nista jednostavniji od klasicne provere deljivosti, nazalost.
broj se rastavi na grupe od po 3 cifre, gledajuci od kraja.
npr. 1|764|527|492, i izracunaju se ostaci tih brojeva po modulu 7
to su, konkretno ovde: 1, 1, 2, 2
zatim se sabiraju, s tim sto se naizmenicno menja znak, i ako se dobije nesto deljivo sa 7, onda je broj deljiv sa 7. Dakle
1+(-1)+2+(-2)=0, pa je ovaj broj deljiv sa 7.
Nije previse korisno, ali je (donekle) interesantno. Inace proizilazi iz toga sto je 1001 mod 7 = -1 (inace, ovako moze da se gleda i deljivost sa 13)
[ Danica Porobic @ 06.01.2005. 19:07 ] @
Samo jedna mala primedba, 1001=7*11*13, tako da je u prethodnom postu verovatno trebalo da pise da je 1000 mod 7 = -1.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|