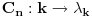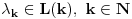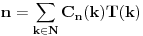[ Dream on @ 14.09.2004. 22:04 ] @
| Dakle imam oktalni broj 142 sa osnovom 8 koji treba prevesti u dekdadni zapis odnosno u osnovu 10. Obrazac je sledeci: 1*8 (2) + 4*8 (1) + 2*8 (0) = 98 P.S. Ovi brojevi u zagradi (x) znaci da je to stepen To mi je jasno, ali ne znam kako se odredjuje koji je broj iz kog sistema, oktalni, dekatni (znam za binarni jer su sve 0 i 1) ali mi nije jasno. Primer: Broj 44446666 iz osnove 8 prevesti u osnovu 16 (to je vec onaj hexadecimalni oblik jer ima 16) Ili ovo: 310 iz osnove 8 u 7 Onim obrascem sa pocetka poruke bilo bi ovako: 3*8 (2) + 1*8 (1) + 0*8 (0) a to je = 200 ali u kom sistemu? Oktalnom sa osnovom 8 jer sam mnozio sa 8? Ili je ovde mozda trebalo da se mnozi ne sa 8 nego sa trazenom osnovom 7? To me zbunjuje. Ako je neko raspolozen da mi napise objasnjenje, mnogo bi mi znacilo. HVALA! |