Hm, šta to znači "geometrijski"? Možda da se z-ovi posmatraju kao vektori? Ajd da probam ovako: za početak, tačke se nalaze na kružnici sa centrom u O(0,0).

Dalje, iz z1+z2=-z3 se može zaključiti da je z3 na simetrali ugla koji obrazuju Oz1 i Oz2: pošto imaju jednake intenzitetke, paralelogram za zbir je romb, pa se dijagonala poklapa sa simetralom. Dakle trougao je jednakokraki.

Pomenuti romb je takav da je kraća dijagonala jednaka stranici, jer je |z1+z2|=|z3|, što znači da su trougli na koje ga deli jednakostranični, ergo, uglevi su po še'set stepeni pa je ugao između z1 i z2 = 120 istih, i eto...

Može lakše

Već vidimo da je centar opisane kružnice dato trougla (čije su koordinate z₁, z₂, z₃) tačka 0, tj koordinatni početak.

Težište možemo dobiti kao
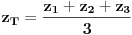
Vidimo da je, po uslovu zadatka, z_T=0

Eh, sad se u tom našem trouglu težište i centar opisanog kruga poklapaju, pa on mora biti jednakostraničan