cekaj, ovo mi lici na resanje domaceg, a zar ti stvarno zelis da ti ljudi odavde rade domace ?

Ajde da ti pomognem, y/2=sin 3x, jel ces nastaviti dalje sam ?

Ja da sam znao da ga uradim ja ovaj zadatak nebi ni postovao ovde, ajd napisi mi postupak...Plz.

Inverzna f-ja polazne f-je dovija se iz sledećeg uslova:
što potiče od operacije kompozicije funkcija:

Dalje je:


Uvodimo smenu:


odakle je

>>

Promenljiva može nositi bilo koju oznaku pa je:


Ovo je kako bi ti tražili na pismenom u srednjoj školi, a inače može da se dobije iz
rešavanjem po , što je Chupcko i mislio kad ti je ostavio onaj hint.

Hvala puno!

ovo je cicika riješila fantastično,čestitam.
Ali može i jednostavnije:samo zamjeni mjesta x i y i gotovo.

A može i geometrijski.Nacrtaj graf u dekartovom koo sistemu,a
onda promjeni oznake osa.X neka bude y i obratno.

da li si siguran da moze da se samo zamene mesta x i y :). ajde uradi f^-1(f(x)) i ako je to x za svako x , onda si mozda i nasao inverznu funkciju.

Doduse za neke funkcije (bar za y=x) moze da se to uradi zamenom mesta :).

Uradis samo refleksiju u odnosu na pravu y=x i dobices inverznu funkciju.

Čitajući stare postove...

Ovo bi bilo sjajno kad bi funkcija sin x imala jedinstvenu inverznu funkciju, tj kad bi bila 1-1. No ona to nije.

Rešenje je svaka funkcija oblika

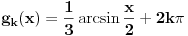
kao i svaka funkcija oblika

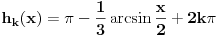
gde je k, naravno, proizvoljan ceo broj.

Kao što vidimo, takvih funkcija ima beskonačno mnogo.