19,709,529,840

Broj koji se sastoji od jedinica iznosi . Obzirom da 9 nije deljivo ni sa jednim od navedenih prostih brojeva, da bi navedeni uslov bio zadovoljen, potrebno je i dovoljno da broj bude kongruentan jedinici po modulu svakog od tih prostih brojeva. Neka je za neki prost broj iz tog spiska za . Niz je periodičan sa periodom po maloj Fermaovoj teoremi. Međutim, to mu ne mora biti osnovni period. Neka je osnovni period tog niza. Rešenje je svaki sadržalac broja .


_{[Ovu poruku je menjao Nedeljko dana 20.11.2012. u 23:35 GMT+1]}

Šta znači "Broj koji je deljiv sa n jedinica"? Da li to znači da je broj deljiv sa jednom jedinicom, deljiv sa drugom jedinicom, ..., deljiv sa n-tom jedinicom? Kolika je vrednost tih jedinica? Opet, ako je reč o brojevima iz skupa prirodnih brojeva onda je svaki broj deljiv sa koliko hoćeš jedinica i jedinica je u skupu prirodnih brojeva jedinstvena (bar je bila).

nisam siguran da sam shvatio što ti je točno niz...




ne razumijem što misliš reći

Evo nekih primera: npr. koliki treba da bude broj oblika 111...1 (n jedinica) da bi bio deljiv sa na primer 7?

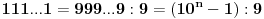
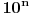
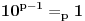
Posto je zakljucujemo da treba da da ostatak 1 posle deljenja sa p. Prema navedenoj teoremi je pa znaci da je .

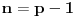
Da proverimo, trebalo bi da je 111111 (6 jedinica) deljivo sa 7: i zaista, .

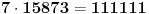
Ono sto malo komplikuje pricu jeste da to ne mora biti najmanji takav broj. Evo na primer za 13: 111111111111 (12 jedinica) jeste deljivo sa 13, ali to vazi i za 111111 (6 jedinica).

Lapsus. Ispravljeno je.

Pa je ostatak pri delenju broja sa . Na primer,

,
,
,
,
,
,
,
,
,
,
,
,
...