Ne znam zašto misliš da imaju FIZIČKI SMISAO sam si rekao da si pronašao definicije
u mat. literaturi, mogao si isto tako da pitaš kakav fizički smisao ima integral ...

Osnovni fizički smisao npr. integrala je površina koju grafik date funkcije (na primer jedne promenljive) formira sa x osom.
Postoji i adekvatno tumačenje prostornih izvoda, medjutim ja nisam dovoljno kompetentna da to objasnim i nadam se da će se javiti neko do naših matematičara da pomogne.

Evo cega se secam (bez kopanja po knjigama):

Ako posmatras planinu kao geometrijski objekat u prostoru, onda je gradijent (vektor definisan kao df/dx*i + df/dy*j + df/dz*k) ima maksimalan moduo na najstrmijoj kosi
planine, bez obzira u kom se geografskom pravcu prostirala.

Ako posmatras bilo koju funkciju tri promenljive, maksimum modula gradijenta ti pomaze
da odredis optimalnu kombinaciju te tri ulazne promenljive.

Gradijent je operator u prostoru funkcija kao što je i integral, ako uzmeš gradijent planine ili čega već i nađeš nekakav moduo dobijena jednačina može da ima fizički smisao ili ne ali gradijent nije fizička veličina koja varira u toj jednačini.

@milanche:

Hvala na tumacenju! Ovako nesto sam trazio i to je ono sto se tesko nalazi u knjigama, a jos teze moze da se cuje od profesora na zvanicnim predavanjima.

Jos su ostali divergent i rotor, pa ako moze neko...

Još jedna sitnica: Ako je funkcija data u implicitnom obliku, recimo u 3D: 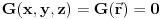, onda je gradijent u tački (x,y,z) vektor normale na tu površinu.

f

Ja znam za fizicko znacenje divergencije i rotora u mehanici fluida. Rotor vektora brzine fluida jednak je dvostrukoj ugaonoj brzini fluida. Znaci da rotor, kako mu i ime kaze, predstavlja nekakvo vrtlozno, rotaciono kretanje.
Ako je divergencija vektora brzine jednaka nuli, onda je fluid nestisljiv, pa bi divergencija predsravljala neku promjenu zapremine.
To je vjerovatno samo jedno fizicko znacenje, jer se u oba slucaja radi o brzini, ali to su jedini primjeri koje znam.

Ovaj primer je dat knjizici (knjizurini) Matematicka analiza II (D. Arandjelovic, Z. Kadelburg) i tice se rotora (posto vidim da te i to zanima a odgovora ima uglavnom za gradijent).
Uocimo tacku koja se krece konstantnom ugaonom brzinom omega oko ose Oz u koordinatnom sistemu Oxyz. Smatra se da je vektor ugaone brzine usmeren u smeru z-ose. Kad se sve to lepo ispise i izrazi vektor polozaja r ove tacke moze se dobiti i brzina (linijska) kao izvod vektora polozaja po vremenu. E sad ono glavno - kad se izracuna rotor ove brzine (linijske) dobije se vektor omega odnosno vektor ugaone brzine. Zakljucak je dakle: Rotor sluzi kao mera rotacije tacke.
Nadam se da ovo pomaze!

Ukoliko je z=z(x,y), gradijent ti pokazuje pravac najvećeg rasta z u datoj tački (najveći nagib). Za ostale stvari možda bolje da pitaš na fizici.

Ako se nalazis u nekom vektorskom polju..znaci ti stojis u tom vektorskom polju,rotor je VEKTOR koji ti govori u kom pravcu ces poceti da se uvijas kao desna zavojnica a samim tim odredjen je i smer...
Npr. Ako rotor ima samo x-komponentu (npr: rot a = 5i)to znaci da ce te to polje u kome se nalazis dovesti u polozaj paralelno sa x osom i poceces da se okreces kao desna zavojnica u poz smeru...

Svaki od ovih prostornih izvoda ima fizicku interpretaciju. Npr divE>0 kaze nam da je ta tacka izvor vektorskih linija elektricnog polja odnosno za divE<0 ponor linija vektora elekticnog polja. Npr. divB=0. Nema ni izvora ni ponora. Rotor recimo ima smisao cirkulacije.