To je fakultetska matematika i kompleksna analiza. Ne moze da se dokaze koristeci samo znanje iz srednje skole. Koliko imas godina?

Verovatno si mislio na Osnovni stav algebre.Ovu teoremu je dokazao Gaus 1815. ali se ne može izvesti na srednjoškolskom nivou.

Zar Osnovni stav algebre nije da polinom n-tog stepena ima tačno n nula u kompleksnom polju? Čovek pita samo za jednu nulu, ostale nisu bitne.

To su valjda ekvivalentne stvari. Ako svaki polinom sa koeficijentima iz nekog polja ima bar jedan koren u tom polju, onda svaki polinom sa koeficijentima iz tog polja ima i faktorizaciju na inearne faktore takođe sa koeficijentima iz tog polja. Sve se može dokazati na bilo kom nivou uz odgovarajuće pripreme. Recimo, ako se zna da je 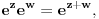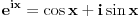, da svaki ograničen realan (a samim tim i kompleksan) niz ima konvergentan podniz, kao i da ako niz 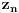konvergira ka 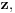da onda 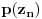teži ka 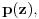gde je 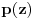ma koji polinom, onda je to dovoljno za dokaz korišćenjem "srednjoškolske" Matematike.

Pa nadji dve tačke u kojima polinom uzima vrednosti različitog znaka.

Plus, ako znaš da ako polinom sa realnim koeficijentima ima jednu nulu u C\R onda je i konjugat tog broja takođe nula polinoma, onda se lako dobija da svaki takav polinom neparnog stepena ima bar jednu realnu nulu.

Dokaži da je deljiv sa x-a :)

Drugi razred srednje skole sam...

Onda ćemo mačo pričekati da naučiš limese i tako to.

E baš pametno.Strašiš djecu limesima.Ajde ti riješi onaj limes sa upisanim mnogouglovima Nedjeljko.(Pa onda se čudimo što djeca
mrze matematiku.)
Ne boj se ti ovih Metalnem,oni se samo prave važni.Kad su išli u drugi srednje
pojma nisu imali šta je to limes.
--------
Svaki polinom P(x)=a(n)x^n+......+a(1)x+a(0),(gdje su eksponenti prirodni brojevi,
a koeficijenti realni) može se napisati i ovako:a(n)*(x-xn)*....*(x-x1)=P(x)
Ako je P(x)=0 onda su oni indeksirani x-ovi nule polinoma.Zato što je za svaki
faktor (x-xi)=0 i P(x)=0.
--------
Ako znamo sve nul-tačke polinoma lako izračunamo polinom.Obratno je teško.
Ti za sada znaš samo ovo :a(2)x^2+a(1)x+a(0)=a(2)(x-x2)(x-x1)
To jest nađeš nul-tačke kvadratne jednačine x2 i x1.E ako si učio nešto
o kompleksnim brojevima (korijen iz negativnog broja) onda si već na konju.
Od šale ćeš dokazati koji polinomi moraju imati bar jednu realnu nul-tačku.

Ako očekuješ pomoć ovde onda si stvarno trebao da se potrudiš da razjasniš situaciju do detalja još u prvoj poruci, a ne mi osim što treba da smišljamo kako rešiti zadatak treba da mozgamo i o tome koja je postavka zadatka. Za početak mi reci kakve koeficijente ima taj polinom, zatim iz kog skupa treba da bude ta nula koju tražiš, i sam dodaj još sve detalje što znaš o zadatku.

To je tačno, ali hajde ti to dokaži. Pitanje bilo kako se to DOKAZUJE u opštem slučaju. Ne možeš u dokazu poći od onoga što treba dokazati. Sve je to lepo što pišeš, samo što ne predstavlja odgovor na postavljeno pitanje.

Pobogu Nedeljko,zar nisi ovo pročitao.A ti zapucao u teoriju koju
ne zna ni njegov nastavnik.

Pročitao sam i smatram da je odgovor koji sam mu dao u potpunom skladu sa tim. On nema dovoljno predznanja da bi mogao da razume odgovor na postavljeno pitanje, i to je odgovor koji mu je većina učesnika dala. No, ti mu kao odgovor nudiš nešto što nije odgovor na pitanje koje je postavio i tvrdiš da se mi samo "pravimo važni". Odgovor će moći da razume kada bude pripremljen za to.

Neka je dat polinom 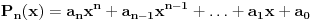sa realnim koeficijentima. Treba dokazati da on mora imati bar jednu nulu u skupu kompleksnih brojeva. Ako dokažemo da on mora imati bar jednu nulu 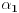ond dolazimo do toga da je on deljiv sa 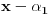pa ga mozemo rastaviti kao 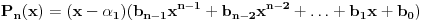. Sada, iz dokaza da polinom mora imati bar jednu nulu, nalazimo nulu 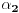polinoma 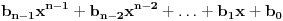itd. I na kraju dolazimo do rastava 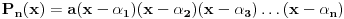koji sledi iz dokaza da polinom mora imati ba jednu nulu.

Super, samo još dokaži da mora da ima barem jednu nulu u skupu kompleksnih brojeva. Već sam ranije napisao da su to ekvivalentne stvari.

@Metalnem
Izvinjavam se što ovo uopšte i pitam, ali šta će tebi to u drugom razredu srednje škole?!
Na ETF-u polinomi se rade u okviru Matematike 1 (po starom programu, da ne bude zabune) i, citiram, "dokaz se ne izvodi zbog složenosti" (Prof. Dragoš Cvetković, "Matematika 1- Algebra").

KOMPLETAN OFF TOPIC:

ljudi, prijatelji, kolege....ne mogu da vam opisem koliko ste mi ulepsali vece. Kao posmatrac sa strane, citajuci postove od prvog do poslednjeg u cugu, ne secam kada sam se smejala toliko. Ovo je stvarno kompletan dozivljaj :) HVALA

TOPIC:
stvarno nemam pojma

Daj, bre, ljudi su već počeli da nas zavitlavaju. Postaćemo glavna zabava: iz čiste zeze će neko da postavi neko pitanje ovde i onda da gleda kako se prepucavamo. Dovoljno je da otvori neki udžbenik matematike i da nabode prstom neku definiciju ili pravilo i onda da naivno pita: a kako/zašto/otkud/itd. ovo.

Onda će se utrkivati ko je napravio najviše buke, gde će se računati index buka/trivijalnost; dakle onaj ko napravi više buke za gluplje pitanje ima prednost.

Na kraju će dva najuspešnija kandidata igrati majstoricu, što će već verovatno zahtevati izvesne pripreme - tipa da se stvarno potrude da nađu neko do yaya zayebano pitanje, vodeći računa o našim profilima i sklonostima, bar onih koji stvaraju najviše echo-a.

Ja se ne slažem sa Konikom i smatram da je Metalnem dobio odgovor koji je za sada odgovarajući. Ako je nekome ova tema zabavna, slobodno neka se zabavlja. Ja se svojih postova ne stidim.

Postovanje

darkosos, Nedeljko, nisam mislila nikoga da vredjam, omalovazavam strucno znanje ili ne daj boze iskazujem nepostovanje. Daleko od toga. Ukoliko ste post tako shvatili, ovim putem se javno izvinjavam. Strucnost i ozbiljnost kojom je odgovoreno na pitanje je samo za pohvalu.

Meni komicna situacija je nastala upravo zbog velike strucnosti kojom su davani odgovori, medju kojima sam se totalno izgubila, i posle svega toga u nastavku, recenice koja glasi: "Drugi razred srednje skole sam...", kao i verovatnog uticaja doba noci kada sam citala post...

Ako sam nego uvredila, nije mi bila namera.

zdr zdr
Cony

(nadam se da si uspela da se odvadiš :)))

A otkud znaš da se taj limes može izračunati tako da se dobije rezultat u obliku koji ti očekuješ. Postoje konstante koje se ne mogu zapisati preko elementarnih funkcija (dakle, kao izraz u kome učestvuju četiri osnovne računske operacije, eksponencijalna funkcija, logaritamska, trigonometrijske, njoma inverzne i tako to) i racionalne konstante. Možda je taj limes baš takav, a možda i nije. Ako ga neko izračuna (to jest predstavi u prethodno opisanom obliku), svaka čast.

@conica
Ma jok bre, i meni je drago da neko ovo nalazi zabavnim :) Moj odgovor je bio u tom smislu; pokušaj da unesem još malo veselja...

Darko, znači li to da sam slobodan da izbunarim poneko zanimljivo pitanje?

Naravno, Dejane. Pa ti si i sam deo ove odgovaračke ekipe, deo mašine :)
Zato postavljaj pitanja kol'ko god ti duša ište. Uostalom, ko mene pa pita... Kad god imam vremena ja se potrudim da odgovorim, a ima tak'ih još.

Nego, nešto sam razmišljao (pravo čudo :). Dosta se ovde energije troši a mislim da može biti i bolje upotrebljena, kad se već bavimo, kako-tako, naukom. Da li neko ima neku interesantnu, originalnu, ideju koja može da se razradi? Da ne bude da samo prežvakavamo ono što piše po udžbenicima.

Vidim da ste se malo odaljili od samog pitanja. Evo pokusacu da "dokazem", tj da ilustrujem dokaz koriscenjem samo high school matematike za drugu godinu. Prvo, nadam se da je autor teme zna sta su kompleksni brojevi. Resicemo najopstiji slucaj kad je polinom sa kompleksnim koef. i trazimo kompleksnu nulu. Sve kompl. brojeve mozes napisati u obliku z=ro*(cos(phi)+i*sin(phi)), kad ro=|z| ide od 0 do +Inf i phi ide od 0 do 2*pi.

Ako je P(0)=0 onda je 0 nula polinoma. Neka je A=P(0)<>0. Neka je sada |z| toliko veliko da je P(z)~=a_n*z^n. Tada kad phi ide od 0 do 2*pi, P(z) priblizno opise krug u kompl. ravni koji obuhvata tacku 0 (0 je centar tog kruga). E sad, kad smanjujes ro, kriva koju opisuje P(z) se smanjuje i deformise (nije vise krug jer P(z) nije vise priblizno jednako sa a_n*z^n), pri cemu tacka 0 i dalje ostaje unutar te krive. Ako je ro pak suvise malo, kriva se vrti oko tacke A, tj 0 je van nje.

Znaci, za neko ro=ro_0 tacka 0 "ispada" iz krive, i tada je na njoj (ponavljam, ovo je sve kako mali Djokica zamislja), a tada je za neko phi_0 P(z_0)=0. Kraj "dokaza". Nadam se da sad bar intuitivno razumes zasto svaki polinom iz C[x] ima nulu u C :).

RgdZ, deXter