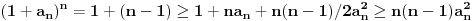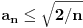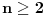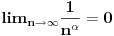|
|
[ Mikky @ 15.11.2004. 23:53 ] @
|
| Zeleo bih da otvorim ovu temu u kojoj bi iskusniji clanovi ovog podforuma davali neke smernice i savete ljudima koji imaju problem sa matematikom na do-diplomskim studijama. Medju njima sam i ja (zbog cega sam inace i pokrenuo ovu temu).
Dakle, molim za konstruktivne predloge kako uci u kostac sa visom matematikom. U pitanju je matematika za tehnicke fakultete (konkretno program sa gradjevinskog fakulteta). Znaci nista preterano kao sto je duboko proucavanje materije na MATF.
Prvo par pretpitanja, zanima me vase misljenje:
Da li postoje neki preduslovi da bi se visa matematika naucila?
Koliki talenat je potreban? (relativno pitanje)
Da li je dovoljna prosecna inteligencija?
Konkretni problemi koje ja imam:
Slabo razumevanje matematickog formalizma. Na primer jako tesko mi je da shvatim sta je to algebarska grupa, prsten, polje itd... iako su to osnove na kojima se zasnivaju mnogo komplikovanije stvari. Kada procitam definiciju polja ja to pokusavam to da zamislim, da stvorim sliku u glavi sta je to "polje" i povezem sa necim "opipljivim" iz iskustva u realnom svetu jer tako najlakse shvatam. Medjutim to su toliko apstraktne stvari van mog iskustva i poimanja da ta "slika u glavi" jednostavno ne moze da se stvori. Po prirodi nemogu da prihvatam stvari "zdravo za gotovo" i bez razumevanja, ali cinimi se da je matematika u sustini takva, i da ako pokusam da je zamislim kao sliku i razumem na ovaj nacin, necu daleko dogurati.
Zatim, nemogucnost izvodjenja dokaza. Cak i kad razumem neki dokaz neke teoreme (sto je redak slucaj jer opet sve pokusam da zamislim i povezem sa iskustvom) nisam u mogucnosti da ga sam posle ponovim. Da ih pamtim napamet - nemogu jer slabo pamtim bilo sta napamet, jedva da imam par telefona u glavi. Naravno to je saljivi razlog, a pravi je da nema smisla matematiku uciti napamet.
Pa ako nemogu da je ucim napamet i nemogu da je ucim sa razumevanjem, da li ima neke nade za mene? Imam prilicno "slab vid" kod nekih stvari kao sto su npr teoreme. Ono sto je nekima ocigledno (ili bar autoru knjige kad kaze "...na osnovu toga lako se uocava da je to i to tako i tako...") meni treba neko vreme da to vidim a verovatniji slucaj je da to nikad ni nevidim.
Jako mi prijaju zanimljivosti i price iz matematike koje citam ovde po forumu od Nedeljka, chupka, t0wka, srkija i ostalih talentovanih ljudi. Price o Euklidu, Lobacevskom, istoriji, primeni i filozofiji matematike veoma golicaju mastu i otvaraju um, ali jako jako retko u knjigama za fakultete naidjem na nesto takvo. Eventualno bude pola strane po glavi neki uvod o tome sta je sledeca oblast i zasto je onda zanimljiva. Ostalo je suva teorija koju pogadjate - nemogu ni da zamislim u glavi. Verujem da je ovakav pristup izlaganja u knjigama ono zbog cega se vecini ljudi dize kosa na glavi kad se pomene matematika, sto nikako ne bi trebalo da je slucaj jer bi svi trebali da znaju matematiku odnosno njenu sustinu. Knjige kao da su pisane za robote koje trebaju da koriste dobro definisana pravila i iz njih izvode nova pravila ne zanimajuci ih zasto je to sve bas tako, kako to sve izgleda i cemu sve to. Da li postoji neka "neobavezna" knjiga iz matematike sa ovim stvarima koju bih citao u slobodno vreme (koga inace nemam)?
Onaj ko je vec "izoblikovan" kao matematicar, iz ovog posta ce shvatiti na koliko niskom nivou matematicke svesti se ja trenutno nalazim, i verovatno koliko je moj pristup celoj stvari pogresan. To me ni necudi, ako uzmem u obzir da se nisam razvijao pod takvim uticajem da od malih nogu razmisljam apstraktno vec prakticno i iskustveno. E onda sam upisao fakultet...
|
[ zvrba @ 16.11.2004. 08:39 ] @
Citat: Mikky:
Prvo par pretpitanja, zanima me vase misljenje:
1. Da li postoje neki preduslovi da bi se visa matematika naucila?
2. Koliki talenat je potreban? (relativno pitanje)
3. Da li je dovoljna prosecna inteligencija?
1. Osnovni. Odlicno baratanje razlomcima, razlomljenim potencijama i logaritmima. Visa matematika (pod time se obicno podrazumijevaju derivacije i integrali) podrazumijeva odlicno baratanje aritmetikom. Za algebru - samo osnovna teorija brojeva. Cesto se koristi "Extended Euclidean Algorithm" (ne znam smisleno prevest "extended").
2. Netko je jednom rekao da je talent manji dio uspjeha, ogroman dio je vlastiti ulozeni trud.
3. IMHO, da. Mozda ce ti duze trebat da 'pohvatas' neke stvari..
Citat: Slabo razumevanje matematickog formalizma. Na primer jako tesko mi je da shvatim sta je to algebarska grupa, prsten, polje itd... iako su to osnove na kojima se zasnivaju mnogo komplikovanije stvari. Kada procitam definiciju polja ja to pokusavam to da zamislim, da stvorim sliku u glavi sta je to "polje" i povezem sa necim "opipljivim" iz iskustva u realnom svetu jer tako najlakse shvatam.
Mislim da ti je tu greska. Ja upravo sad na postiplomskom studiju ucim algebru.. trenutno grupe. Uopce se ne zamaram primjenom i pokusavanjem povezivanja sa realnim svijetom. Ono, imas osnovnu definiciju grupe, iz koje proizlaze neki osnovni teoremi iz kojih proizlaze drugi itd.. kad dovoljno duboko udjes u teoriju, primjena se sama pojavi :)
Citat: Zatim, nemogucnost izvodjenja dokaza. Cak i kad razumem neki dokaz neke teoreme (sto je redak slucaj jer opet sve pokusam da zamislim i povezem sa iskustvom) nisam u mogucnosti da ga sam posle ponovim.
Hm. Ja sam imao isti problem na faxu. Imao sam 5 iz svih analiza, 4 iz diskretne matematike, al dokazi su mi uvijek bili problem. 7 godina kasnije sam pogledao neke dokaze i puno lakse bih ga rekonstruirao sada nego tada..
E da, uzmi u obzir da je autor knjige doktor matematike i kad kaze da je nekaj "ocito", to moze biti vrlo netrivijalna stvar koja se raspisuje na par strana (i u biti je vjerojatno neki teorem za sebe za koji se pretpostavlja da ga citatelj zna). Koliko je nesto "ocito" ovisi o autoru knjige, razini na kojem je pisana knjiga i o samom citatelju i njegovom predznanju. Tako da ocito moze (stvarno trivijalno) zbilja slijediti iz definicije, moze bit malo pisanja ili stvarno par strana. Ne treba te obeshrabrit kaj ti "ocite" stvari nisu jasne :) Nabavi "laksu" literaturu, pitaj kolege koje to bolje ide, odi profesoru na konzultacije da ti popuni rupe.. uglavnom, ak se potrudis, uspjet ces.
Tada sam pamtio sve detalje u dokazu.. sto je bila greska (jest da sam ih naucio za ispit, ali vrlo brzo zaboravio). Sad kad "ucim" dokaz, procitam ga u knjizi, paralelno ga raspisujem na papiru, pokusavam popunit rupe i opravdati sve korake, i na kraju ga skratim u neki "visi" opis ideje dokaza.. Onda zapamtim ideju umjesto svih sitnih koraka i tako ide.. Dokaz onda u biti postaje kao serija rjesavanja jednostavni(ji)h zadataka za vjezbu... pa na temelju ideje pokusam rekonstruirat cijeli dokaz opet.. i tak.. puno pisanja da "udje u glavu". vjerujem da se s vremenom kolicina potrebnog pisanja smanjuje jer se polako "istreniras" za taj nacin razmisljanja..
Uostalom, ako ti nije bitna ocjena, zasto se zamarati sa dokazima? (istina, ne znam kakav je rezim kod vas, ali ako nije matematicki fax, ne vjerujem da ce profesor za 2 ili 3 traziti ikakav dokaz..). Na FER-u je za nizu ocjenu na usmenom bilo dovoljno znat osnovne definicije i rjesit kakav jednostavni zadatak.
[ zzzz @ 16.11.2004. 23:51 ] @
Dobra je ovo tema Mikky,čestitam.Odgovoriću čim nešto smislim
i uhvatim vremena.Ima ovdje priličan broj dobrih matematičara
pa ako svaki po nešto kaže možda pomognu mnogima.
[ MixMaster @ 16.05.2005. 22:43 ] @
Ovu temu sam vec nekoliko puta provjeravao i, bas mi je zao sto se prica nije nastavila.  Evo jos jednom pozivam ljude da odgovore na postavljeno pitanje, i pomognu drugima, koje matematika interesuje, ali se ne snalaze najbolje u njoj.
Pozdrav. [ Mikky @ 17.05.2005. 00:15 ] @
Slazem se da bi tema bila jako korisna, pogotovo nama koji nismo toliko talentovani za matematiku a na ovaj ili onaj nacin moramo da je znamo (npr studenti ostalih tehnickih fakulteta).
MixMaster, hvala sto si oziveo temu :)
[ sekretar SkOJ-a @ 17.05.2005. 22:07 ] @
Lancelot Hogben
[ Gn0m3 @ 18.05.2005. 17:04 ] @
Mozhda ce ovo shto cu napisati zvuchiti suludo ali probaj upravo sa knjigam s MATF-a!
Poenta je u tome shto se u matish na nashem faxu ulazi dosta dublje i stoga su neke stvari koje su izostavljene ( a to su najchesce objashenja :) iz vasheg nastavnog programa lepshe odradjene u nashim knjigama.
Konkretno, ja dolazim iz Makedonije i u nashoj gimnaziji ( matematichka btw! ) nismo odradili ni jedan integral i nijedan izvod! Sada sam na prvoj godini MATF-a i nemam nikakvih problema ( sem shto me ponekad zamrzi da uchim :) s Analizom. Slichno vazhi i za Algebru :)
[ KPYU @ 18.05.2005. 20:45 ] @
Čitava ideja matematike je da se ona uči od početka, tj da imaš solidan fond poznatih stvari kojima barataš jako dobro, e da bi se usudio da uđeš u šumu nepoznate matematike.
Sam fond poznatih stvari nije dovoljan, naravno, već to znanje mora biti lepo sistematizovano, tj nije dovoljno znati da nešto jeste, nego i zašto jeste.
Svi su upoznati sa jezikom celih brojeva. Tu imamo neke operacije (+,-,*) neke pseudo-operacije (/, ^), neke relacije (<,>,=,|), te neke elemente (0,1). Međutim to su celi brojevi. Da imamo neke druge elemente, da li bi sve ostalo isto ? Šta tu zavisi od samog skupa Z, a šta od operacija, relacija,... Da bismo to videli potrebna je apstrakcija. Trebamo sve da apstrahujemo, da se oslobodimo samog poznatog skupa i pojedinih operacija. Da idemo korak po korak.
Formalizacije se, s toga, uvode da bi nam pokazale neka određena svojstva. Teoreme pokazuju da se nova svojstva mogu svesti na stara svojstva. Tražeći model koji zadvoljava svojstva nećemo postići puno. U svakom modelu postoji gomila specifičnosti koja više ne zavise od samih svojstava.
Većina ljudi smatra da je Euklidska geometrija potpuno jasna. No ukoliko posmatramo takvu geometriju bez axiome paralelnosti (npr Plejferov oblik: Ako imamo zadatu pravu i tačku van nje, u ravni određenoj tom pravom & tačkom postoji jedinstvena prava koja sadrži tačku i nema zajedničkih tačaka sa zadatom pravom) dobijamo apsolutnu geometriju. U apsolutnoj geometriji ne važe mnoge stvari koje važe u Euklidskoj. Eh, sad neko može kazati "A šta će meni te neeuklidske geometrije". Odgovor je jednostavan i glasi "Na ovoj planeti nema Euklidske geometrije". Svi znamo da, ukoliko dovoljno dugo idemo u jednom pravcu, vratićemo se u istu tačku.
Matematiku treba učiti lagano. Početi od jednostavnih stvari, videti šta zavisi od čega. Zatim to treba zapamtiti. U matematici se stalno pozivamo na jednostavne slučajeve. U konkretnom zadatku gledamo da zadatak svedemo na konačan niz jednostavnih koraka koje znamo da uradimo. Ukoliko ne znamo, nećemo uspeti da rešimo zadatak.
Npr kod integraljenja zadanih f-ja moramo znati postupak smene, parcijalne integracije i tabličnih (osnovnih) integrala. Dalje ćemo integral bilo koje funkcije, gledati da svedemo na integral neke poznate f-je. Što ih više znamo, lakše ćemo uraditi integral. Neke f-je nemaju lep analitički zapis. Treba i njih znati.
[ Cabo @ 25.05.2005. 13:00 ] @
Citat: KPYU:
Matematiku treba učiti lagano.
E, upravo to jeste i glavni problem. Da bi matematiku izučavao čovek prosečne inteligencije i sposobnosti, koji je uz to „tabula raza“, odnosno poznaje samo osnovne operacije sa npr. polinomima i skupovima, a ne zna baš ništa o integralima, matricama i izvodima, potrebno je mnoooogo vremena. Međutim, od studenata se očekuje da sve to savladaju za samo 4 godine. Meni je bilo potrebno toliko samo da bih u potpunosti shvatio šta je to Analiza i da bih njom ovladao toliko da mogu da pratim kurs Analize II.
Citat: KPYU:
Npr kod integraljenja zadanih f-ja moramo znati postupak smene, parcijalne integracije i tabličnih (osnovnih) integrala. Dalje ćemo integral bilo koje funkcije, gledati da svedemo na integral neke poznate f-je. Što ih više znamo, lakše ćemo uraditi integral. Neke f-je nemaju lep analitički zapis. Treba i njih znati.
Tačno. I napomenuo bih da u nekim oblastima matematike, kao što su integrali, ili redovi, postoji „kvaran“ princip: „Kako si se samo setio rešenja?“ „Nema pravila. Moraš uraditi što veći broj zadataka i nabubati rešenja. Onda ih samo kombinuješ i to je to.“
[ KPYU @ 25.05.2005. 23:55 ] @
No, ako neko dolazi kao tabula rasa, da li to znači da je nepismen ili samo funkcionalno nepismen.
Još jednom napominjem, podrazumeva se neko elementarno (u ovom slučaju srednješkolsko) znanje. Ukoliko takvog znanja nema, govorimo o funkcionalnoj nepismenosti.
Stoji činjenica da Anlizu I najbolje shvatiš dok spremaš Analizu II
Daklem, ako želiš da naučiš AN I, moraš znati šta radiš, zašto radiš i kako radiš.
Ako imaš rupe u znanju, potrudi se da ih popuniš.
NEMOJ ZABORAVLJATI ONO ŠTO SI NAUČIO
Nemoj odustajati.
Ovo poslednje je jako važno.
Većina ljudi kaže: "Ja ovo ne znam, niti ću ikad naučiti. 'Ajmo na pivo. ". Pa posle 2 godine kaže: "Evo već dve godine učim."
Dakle nije važno učiti nego naučiti
Meni je, lično, pomoglo to što sam pred svaki ispit imao ljubavnih problema, te nisam išao na pivo.
[ ~stojko~ @ 27.05.2005. 18:53 ] @
Zanimljiva i kvalitetna rasprava cini mi se. Pozdrav svim sudionicima i "koja" rijec od mene...
Citat: Mikky Kada procitam definiciju polja ja to pokusavam to da zamislim, da stvorim sliku u glavi sta je to "polje" i povezem sa necim "opipljivim" iz iskustva u realnom svetu jer tako najlakse shvatam. Medjutim to su toliko apstraktne stvari van mog iskustva i poimanja da ta "slika u glavi" jednostavno ne moze da se stvori. Po prirodi nemogu da prihvatam stvari "zdravo za gotovo" i bez razumevanja, ali cinimi se da je matematika u sustini takva, i da ako pokusam da je zamislim kao sliku i razumem na ovaj nacin, necu daleko dogurati.
Ne vjerujem da je matematika u sustini takva. Osim toga ti kao buduci inzinjer radis kako i treba. Pokusavas matematiku svrsishodno primjeniti, jer nama inzinjerima matematika tome i sluzi. Spomijes prethodno neke algebarske grupe. Ja ne znam sto je to. Treba li vam to u gradjevinarstvu? Mozda su to matematicari ubacili u gradivo, jer im je zanimljivo, a to sto je inzinjerima beskorisno previse ih ne brine.
Citat: MikkyZatim, nemogucnost izvodjenja dokaza. Cak i kad razumem neki dokaz neke teoreme (sto je redak slucaj jer opet sve pokusam da zamislim i povezem sa iskustvom) nisam u mogucnosti da ga sam posle ponovim. Da ih pamtim napamet - nemogu ... nema smisla matematiku uciti napamet.
Pa ako nemogu da je ucim napamet i nemogu da je ucim sa razumevanjem, da li ima neke nade za mene?
:) Svaka cast!
Ja sam inace asistent elektrotehnike i tu i tamo neki elektricki izvod i znam. Muce me isti problemi kao i tebe i mucit ce jos bar neko vrijeme. Izvodjenje i dokazivanje sigurno ima nekog smisla, no meni nije uvijek sasvim jasno kakvog.
Ovdje se nitko nije osvrnuo na katastrofalno lose profesore matematike. Oni uopce ne pokazuju dobro svojim ucenicima/studentima koji je smisao matematike. Razloga je vise:
1. Ni sami ne kuze gdje je mjesto matematici i ne razumiju ju.
2. Ako znaju nesto pod 1, onda ne znaju koja je svrha matematike u gradjevinarstvu, elektrici, strojarstvu ili tamo gdje se vec koristi.
Kada bi ti dobar znalac pokazao gdje se te algebarske grupe koriste u gradjevinarstvu, vjerovatno bi to puno brze leglo.
Citat: MikkyImam prilicno "slab vid" kod nekih stvari kao sto su npr teoreme. Ono sto je nekima ocigledno (ili bar autoru knjige kad kaze "...na osnovu toga lako se uocava da je to i to tako i tako...") meni treba neko vreme da to vidim a verovatniji slucaj je da to nikad ni nevidim.
:) Slab ti je vid na jednom drugom polju. A to je da samo ne znas kako ti problemi muce i druge. Kad u knjigama pisu da je nesto ocigledno, tada to ne mora znaciti da bi student to trebao lako uvidjeti. Knjiga mora drzati "nivo" pa se u njoj ne smije objasnjavati svaka jednostavna stvar. Ili bi knjiga bila preopsirna. Ili autor uopce nije napisao dobru knjigu. Ili...
Ili kad na satu nastavnik kaze da je nesto ocigledno, mozda skriva svoju nesigurnost ;)
Sto se tice ociglednosti, mogu jos reci da mnoge stvari stvarno jesu ocigledne, samo je pitanje kome. Onima koji znaju gdje tocno treba gledati, sto traziti i kako traziti.
Dobar nastavnik matematike ti u 5 minuta moze otvoriti oci, a ako to istrazujes sam (ili ja, svejedno) onda to moze potrajati, 10 100, 1000 puta duze ...
[ ~stojko~ @ 27.05.2005. 19:11 ] @
Nastavljam...
Citat: Mikky
Jako mi prijaju zanimljivosti i price iz matematike ... ali jako jako retko u knjigama za fakultete naidjem na nesto takvo.
To znaci da profesori matematike kako vec rekoh ne znaju dobro ono sto nas poducavaju, a ne znaju to dobro ni prezentirati. I isto sam vec rekao da knjige moraju zadovoljavati neke nonsens principe.
Nasi matematicari mahom predaju matematiku za matematicare, jer su je i ucili na fakultetu za matematicare. Ja isto imam problema kad trebam objasniti struju neelektricarima. Kad pricam elektricarima lako se izvucem sa "to vec kuzite", "to ste trebali znati" i sl ...
Cinjenica je da bi jedan dobar gradjevinar bolje ti ispredavao matematiku nego profesor matematike ...
Citat: Mikky
jer bi svi trebali da znaju matematiku odnosno njenu sustinu. Knjige kao da su pisane za robote koje trebaju da koriste dobro definisana pravila i iz njih izvode nova pravila ne zanimajuci ih zasto je to sve bas tako, kako to sve izgleda i cemu sve to. Da li postoji neka "neobavezna" knjiga iz matematike sa ovim stvarima koju bih citao u slobodno vreme (koga inace nemam)?
Mislim da sustinu matematike donekle znamo na pocetku osnovne. Poslije kad Prestanu zadaci rijecima i kad se pocne vjezbati samo cista tehnika izracunavanja ode sve stranputicom. Ne mogu se integrali i derivacije uciti tako da se vjezba racunanje stotina zadataka. Treba znati u kojoj situaciji uopce se moze iskoristiti integral i derivacija,a to matematicari ne naglasavaju dovoljno.
U Zagrebu ima superzanimljiva knjiga "Pogled u povijest matematike". Autori su Znam i drugi. Cesi. Bavi se matematikom od Arapa i Grka pa do 20. stoljeca i da se iz nje cak i puno nauciti sama matematika.
Inace medju elektricarima je na cijeni markoviceva (BG) visa matematika...
Citat: MikkyOnaj ko je vec "izoblikovan" kao matematicar, iz ovog posta ce shvatiti na koliko niskom nivou matematicke svesti se ja trenutno nalazim, i verovatno koliko je moj pristup celoj stvari pogresan. To me ni necudi, ako uzmem u obzir da se nisam razvijao pod takvim uticajem da od malih nogu razmisljam apstraktno vec prakticno i iskustveno.
Sipak pogresan. Inzenjerima (i svakome drugom-osim mozda samim matematicarima) matematika jedino moze i ici prakticno i iskustveno.
Inace ni ne kuzim bas kaj to znaci apstraktno. Valjda mi je to previse apstraktno ;)
[ cure126 @ 08.09.2005. 00:16 ] @
ljudi, ja bas mislim da tamo de se pominje apstraktno i gde se problemi resavaju diskretno, ne treba da se mucimo da nadjemo nesto u realnosti, nesto prakticno. ja sam na pmf-u i tu nam je bas odvojena matematika od informatike posto smo informaticki smer a svi vucemo na informatiku, a profani iz matematike potenciraju matematiku, ali realno za informatiku nam nije koristilo ni 2% ono sto ucimo iz matematike. e sad zasto je ovo bitno za temu? zato sto vecina mojih kolega ustvari uce matematiku na cake, bez nekog duboookog razumevanja, nego samo da prodju. mislim to se po pismenima i usmenima neda provaliti ali znam kako mi jedni drugima pomazemo sa ucenjem tih fora i znam kako ja ucim. evo npr za tu cuvenu analizu 1 kad skontas samo malo kako funkcionisu integrali, diferenciranja i to sve, za resavanje integrala ti ne treba da znas njegovu def i na kraju sve ono sto mi treba da znam stane da dopisem na papir gde su mi tablice integrala i diferencijala i jos malo vezbanja i moze se dobiti 75 od 100 poena. mislim, treba razumeti matematiku, ne moze se to bubati, ali ne treba se previse patiti s tim nalazenjem primera u praksi. a sto se tice dokazivanja teorema i ostalog neko od vas je vec rekao da treba pisati pored na papir dokaz i kontati zasto je sta i popunjavati rupe sa pomoci sa strane ili nesto, ali najlakse ih je zapamtiti kad se razumeju. ali ne treba stvari izvlaciti u nas svet nego mi da udjemo u svet analize ili algebre ili cega vec. nadam se da sam reko nesto i pametno. 
inace tema je jako dobra. [ Alexsis @ 29.04.2008. 23:44 ] @
Mikky Kao da opisujes mene!
Ali ja sam shvatio da sve te apstraktne stvari za inzenjersku struku i uopste za praksu su nepotrebne i samo zamaraju studente nepotrebno. Samo mi nije jasno kad ce bre to neko da shvati i da izvrsi neku reformu ili sta vec.
Ja polazim od toga da sve sto je komplikovano i apstraktno je lose obijasnjeno!! Evo citam ove knjige od G. Milovanoica i skoro da je nista ne razumem bas zbog nacina na kome je pisana {Kao da je pisana za robote a ne za studente} dok citajuci neku knjigu od Apsena sve mi je jasno!!
Ali dzabe mi Apsen kad je program za polaganje iz Gradetove knjige i sad ne znam sta da radim...
Znaci uglavnom su za sve krivi oni sto pisu program{Kakv je to program na kome inzenjeri uce osnove matematicke logike, boli ga ku...)jer da sam hteo da upisesem matematiku iso bi na pmf a ne na neki tehnicki fax...
[ Duka91 @ 02.05.2008. 23:40 ] @
Ja imam problem što matematiku radim nekako mehanički.
Izvežbam par zadataka i onda njih tražim u ostalima tj. pokušavam da ih rešim šablonski.
Profesor kaže da to ne valja. Ne znam zašto ali kao da sam stao na Code:
x + 5 = 20 pa onda znam da od desne strane treba da oduzmem poznati sabirak da bih dobio x i onda to pravilo primenjujem u narednih 100 primera. Ali sada kod kompleksnih zadataka to ne pali :(
Sada radimo trigonometriju i ja uporno tražim neko pravilo koje bi mi pomoglo da rešavam te zadatke međutim slaba valjda.
I ja pokušavam da to shvatim praktično jer u predmetima gde to mogu nemam problema.
Npr. radili smo logaritme i sve je to u redu, shvatim ja kako se radi, izvežbam dosta zadataka i na pismenom dosta dobro uradim zadatke ali sednem kući i zapitam se šta je uopšte logaritam, šta radim sa tim brojeima? Nemam odgovor...
Možda je kriv i profesor što nam nije objasnio to na bolji način.
I još nešto, u matematici nema šta da me privuče da rešavam zadatke kao što me privlači u programiranju.
Ako pišem neki program, pišem ga sa ciljom da bi radio to što ja hoću. Ispišem linije i linije koda i na kraju imam to što sam na samom startu i želeo, dok kod matematike toga nema. Rešavam jedan zadatak na dve strane da bih na kraju dobio je*eno X. Jednostavno ne vidim kada će mi to sve zatrebati. Verovatno grešim ali ne mogu to da izbijem iz glave.
Razlog zbog čega sve ovo pišem je da vidim da li vi imate neki savet koji bi mi pomogao. Možda imam pogrešan stav prema matematici?
Stvarno ne znam kako da matematiku približim sebi.
[ Alexsis @ 04.05.2008. 01:00 ] @
Ma kolko ja vidim nema tu neke filozofije il si rodjen za matematiku ili nisi. Ukoliko jesi ona ce ti lakse ici i verovatno ces je zavoleti ako nisi onda ulazis u probleme...
Matematika na nivou srednje skole, nije teska da se nauci tu prvenstvenu ulogu ima profesor, ako imas dobrog progesora i ako ga slusas 50% posla si odradeo!
Ovde se akcenat baca na teoriju vise matematike za koju trebas da imas nekakav nacin razmisljanja koji imaju samo neki ljudi koji se bave time {profesorei} a traze od nas da i mi to znamo sto naravno nama nikad nece trebati osim ako se ne bavimo matematikom...
[ markozelenovic @ 04.05.2008. 10:36 ] @
Citat: Ma kolko ja vidim nema tu neke filozofije il si rodjen za matematiku ili nisi
Niko se nije naucen rodio.
Citat: ako imas dobrog progesora i ako ga slusas 50% posla si odradeo!
75% [ Bojan Basic @ 04.05.2008. 11:45 ] @
Ne baš, jer ipak ne može svako da se bavi svačim, već razne osobe imaju različite talente (a s tim se rađaju). [ galet@world @ 05.05.2008. 19:59 ] @
Ono u zagradi je diskutabilno. Da li to znači da su talenti nasledni?
[ Bojan Basic @ 05.05.2008. 20:33 ] @
Ne bih sad da zapadnemo u neke duboke psihološke zaključke, pa ćemo ovako. Uzmi jedan razred u osnovnoj školi. Tokom prve četiri godine školovanja njima sve predmete predaje ista osoba (učitelj/ica), pa opet nekom jedan predmet ide bolje a drugi lošije, a nekom obratno. To odmah obara tvrdnju da nečija ljubav prema nekom školskom predmetu zavisi samo od toga kako mu je taj predmet prezentovan tokom školovanja.
[ Alexsis @ 06.05.2008. 00:06 ] @
A sto nas bre onda ovolko smaraju sa matematikom na tehnickom fakultetu, mislim stvarno bez razloga...
[ momsab @ 06.05.2008. 00:53 ] @
tehnika ne moze bez matematike ;)
[ Alexsis @ 06.05.2008. 00:59 ] @
Naravno da ne moze ali kad bi ti znao kakve sve mi gluposti ucimo...
Pa za to i ljudi beze od tehnike!
[ galet@world @ 06.05.2008. 21:01 ] @
Citat: Bojan Basic:To odmah obara tvrdnju da nečija ljubav prema nekom školskom predmetu zavisi samo od toga kako mu je taj predmet prezentovan tokom školovanja.
Deca su "školovana" i pre škole - smatram da je ta "škola" presudna u formiranju ljubavi
prema nekim stvarima koje su u školi na određen način samo konkretizovane. Ipak mislim
da uticaj lošeg učitelj - a/ice može biti poguban na stav deteta prema njegovoj ljubavi
Citat: Alexsis: Naravno da ne moze ali kad bi ti znao kakve sve mi gluposti ucimo...
Pa za to i ljudi beze od tehnike!
U matematici nema gluposti. Postoje mnoge stvari u tehnici za koje još nema precizne matematičke definisanosti.
Zato i koristimo empirijske (iskustvene) pokazatelje. Koliko god naučiš matematičkih "gluposti" nikad nećeš preterati. [ Astek @ 06.05.2008. 21:42 ] @
1. Glavni problem je u našim srednjim školama. Matematika se uči uglavnom šablonski - prepoznavanjem i prisecanjem zadataka rađenih na času ili kući a ne rešavanjem istih. U većini srednjih škola skoro se potpuno zanemaruje logičan sled stvari definicija-primer-teoreme sa dokazom. Zato dosta srednjoškolaca pomisli da zna šta je matematika .
2. Ne bih želeo da budem grub, ali rad i upornost mogu dati rezultata do neke granice. Ako i pored rada , neko ne uspeva da reprodukuje dokaz , teško da će uspeti da sam izvede dokaz nekog nepoznatog tvrđenja na pismenom delu ispita(recimo iz Teorije grupa). Ja nekako matematiku povezujem sa sportom. Neko može a neko i ne.
[ Ojler @ 09.05.2008. 12:36 ] @
Slazem se sa Astekom da se u nasim skolama matematika shvata vise kao jedna vezba, dril a ne
kao jedna duhovna disciplina. Mnogi koji imaju dobre ocene iz srednje skole misle da znaju matematiku,
a veliki broj njih nije nikada ucio teoriju i dokaze. Vazno je resavanje zadataka, ali to nije jedino sto djaci treba da znaju.
To je isto kao sto neki znaju da sviraju, a ne znaju note. Nasi djaci su sluhisti.
Zasto je to tako ima vise razloga. Od ustaljenog nacina rada, do otpora same dece prema matematickoj teoriji i zahtevnog programa.
[ MixMaster @ 09.05.2008. 23:00 ] @
"Neko moze a neko ne"??? Hm...ne bih da zvucim uvredljivo, ali mislim da to nije tacno...hm...ni najmanje.
Ajde da ne pisem previse, samo cu ispricati u kratko sta se desavalo sa mnom... Dakle, pred kraj osnovne skole i pocetkom srednje dolazio je porodicni prijatelj da mi pomaze oko matematike. Jednostavno, nikada na casu, nisam cuo ni jednu pricu koja bi me zainteresovala za matematiku...nisam cuo price o Euklidu, Arhimedu...nisam cuo ni jedno objasnjenje koje bi mi dokazalo da se komplikovanije stvari iz matematike mogu negdje i prakticno primijeniti. Drugim rijecima, sve je predstavljano "apstraktno" (sta god to u stvari znacilo).
Kasnije...posto sam postajao sve zainteresovaniji za tehniku, shvatio sam da iza prakticnih stvari, u istoj, mora postojati neka teorija. Nezavisno od fakulteta (na ljetnjim pauzama) ja sam sjedio i citao o raznim stvarima...tipa: integrali, izvodi, diferencijalne jednacine, gradijent....... Dok sam citao, sa strane sam piskarao DIO PO DIO teoreme koju bih citao. Na svoje zaprepascenje  vrlo lako sam shvatio prakticno sve sto sam krenuo da ucim. Sada, kada razgovaram sa elektronicarima, fizicarima i matematicarima, osjecam veliku sigurnost sto se tice tih stvari koje sam sam do sada presao (planiram da ovog ljeta nastavim sa takvim ucenjem).
Dakle, fakultet valja zavrsiti (to sebi stalno govorim  ) ali se sigurno necu oslanjati na "znanje" koje mi "daju" odredjeni profesori, a mislim da ni vi ne bi ste trebali. To neka bude moj savjet vama. Imate popularne knjige, imate ovaj forum (izmedju ostalih), imate domacu i stranu(!) literaturu (u pdf-u ili papirnom izdanju)...citajte...
Pozdrav.
p.s. Vecina dokaza i objasnjenja iz literature sa matematickih ili tehnickih fakulteta moze se objasniti u nekoliko rijeci studentima tehnickih fakulteta. Eh, samo kada bi ste znali kolika je to istina  
p.p.s. Je li "bi ste" treba da bude spojeno"?  [ Astek @ 13.05.2008. 11:34 ] @
Citat: MixMaster: "Neko moze a neko ne"??? Hm...ne bih da zvucim uvredljivo, ali mislim da to nije tacno...hm...ni najmanje.
Dakle svi mogu? Svaki prosečan srpski srednjoškolac može da recimo savlada Teoriju grupa sa svim onim silnim teoremama i dokazima? Možda je i tako . Ipak smo mi zemlja čuda.
P.S: Ja ipak tehniku integrala i diferencijala ne smatram vrhunskim dostignućem u matematici.
[ Nemanjich @ 13.05.2008. 20:46 ] @
Znam da nije deo teme, ali me interesuje (nemoj pogresno da me shvatis) zbog cega ti to nije vrhunsko dostignuce?
Sta je po tvom misljenju vrhunsko dostignuce u matematici?
[ Huemaj @ 13.05.2008. 20:50 ] @
Veliki pozdrav!
Mislim da je to sve u domenu onog dijela nas koji jos nijedan psiholog nije objasnio niti ce mozda uspjeti objasniti, pri tome mislim na trenutke inspiracije kada se rijesavaju nevjerovatni problemi gdje subjekt "vidi" sliku rijesenja na svom "mentalnom ekranu". Sam Einstein je rekao da je intuicija jedino sto zaista vrijedi. Mozda matematicari ili elektronicari ili informaticari ili daktilografkinje ili zidari raspolazu tom intuicijom najveci dio vremena pa odlicno rade svoj posao. Ja sam krenuo sa 6 godina u skolu i bio sam najmladi u razredu, imao sam skoro sve negativne ocjene, jedva sam prolazio prvih godina, ali sam uvijek bio najbolji matematicar jer sam bio tjunovan da mogu da vidim rijesenja i razumijem probleme. Mislim da je tu uzrok i rjiesenje problema, u tome kako smo tjunovani ili podeseni da intuitivno spoznamo rijesenje problema. To se vjerovatno desilo svima nama cesto puta, razbijate glavu oko nekog problema i kad odlozite papir i olovku "ugledate" rijesenje problema, ja licno bih mogao navesti iz rukava nekoliko primjera kada mi se to desilo, bukvalno u trenutku kad sam odlagao papir i olovku na sto rijesenje je bilo tu na tacni.
Moje je licno misljenje da nije ispravno uciti mehanicki rijesavati probleme, to me podsjeca na dozu hipnoze. Vjerujem da nije dovoljno nauciti rijesavati zadatke iz ovoga ili onoga, jer cim se promijeni kontekst izgubicemo se. Mislim da je potrebno da se covjek osposobljava da razmislja na odredjeni nacin, da ima tu ostrinu uma ili koncentraciju (nesto kao kad pricate na jednom jeziku pa onda na drugom, znaci taj klik' u glavi). Ali ako se naucimo da razmisljamo ao matematicari (ili elektronicari ili - ili...) onda cemo sa tom ostrinom uma pristupati svakom problemu. Neko je ovdje pitao sta znaci apstraktno razmisljanje. To je razmisljanje van svakog konteksta ali koje se moze primjeniti na svaki moguci kontekst. Zato mislim da reci da matematika zahtijeva apstraktno razmisljanje je stereotip koji je neki nematematicar davno pustio u opticaj :) jer je matematika formalna a abstraktno je antipod od formalnog
Mislim da ima istine u tome da je nas stav prema matematici pogresan, ali ili cemo se sami pribliziti matematici ili ce nam je neko drugi nabiti na nos pa cemo je zavoljeti :)
Imam jednu interesantnu pricu, radi se naime o sljedecem: jedan moj rodjak je isao u osmi razred, tada se bas upregao da dobije prosjek jer mu je trebao prosjek za srednju koju je htio da upise. Ali imao je grdnih problema tokom citave osnovne skole sa matematikom. I zamolio me da mu pomognem da rijesi par zadataka, i to onih tipicnih "problema", gdje imate tekstualno definisan problem i morate da iznadjete put do rijesenja. Radilo se o nekih 38 zadataka koje on nikako nije mogao da rijesi. Od tih 38 zadataka nekih 16-17-18 je rijesila jedna njegova komsinica koja je studirala sa mnom, ali u tih 17-18 zadataka sam prepoznao nevjerovatnu podudarnost: svih tih 16-17 zadataka su se mogli rijesiti primjenom postojecih formula, znaci radilo se o sablonskom rijesavanju zadataka. Medjutim, tamo gdje formule ne pomazu vise, gdje se covjek morao otisnuti od postojecih obrazaca i osloniti se na svoju logiku i tu naostrenost uma i prakticno razmisljanje, tu je ta djevojka kiksala. Taj rodjak je ocekivao od mene da mu kazem formule i carobne mantre kojima ce moci rijesiti te zadatke a ja sam ga umjesto toga motivisao da razmislja o zadatku samom, a ne da odmah pocne da kopa po formulama (zato vjerujem da je potrebna i ta neka motivisanost da se suocim sa problemom, "sharp edge" :)). I na kraju je on takoreci sam rijesio sve i jedan zadatak, odjednom su mu pricinjavali super-zadovoljstvo, decko je prezentirao svoja rijesenja u skoli, profesorica se zacudila kako je dosao do rijesenja nestandardnim putem, po prvi put je zavrsio sa najvisom ocjenom iz matematike i upisao je srednju koji je zelio. Ja sam ga samo "natjerao" da zauzme stav pri rijesavanju zadataka.
Matematika nije samo rijesavanja zadataka ili jos jedna prepreka do diplome. Ko tako razmislja nece nikad biti dobar inzinjer. Matematika je jedan aspekt nacina na koji funkcionise ovaj univerzum, a univerzum je jedno cudo, jedan savrseno izbalansiran sistem. Da mi vjerujemo u haos zar bi ijedan naucnik radio svoj posao? :) Einstein je jednom rekao nesto tipa: "Postoje dvije vrste ljudi: oni za koje nista nije cudno (citaj profano) i oni za koje je sve cudo"
Slazem se da je potreban dodir sa praksom, oni nam pomazu da razumijemo kompleksnije koncepte. Ja na primjer sam imao poteskoca da razumijem prostornu geometriju, jednacine ravni i tako dalje. Cesto puta sam pokusavao da prozrem to sve, ali mi nije polazilo za rukom. Iako sam mogao da rijesavam zadatke falio je onaj klik' u glavi, kada osjecate da nema vise tajni, kao da to sto ste otkrili pripada samo vama (Evo kod mene jos uvijek ta knjiga u zadnjoj fazi raspada, "Zbirka zadataka iz matematika" od Branislava Stojanovica :) ) I prije par mjeseci radim ja ray-tracing iz kompjuterske grafike i na jednoj grafici je opisano rijesenje jednog problema vektorski. I u jednom trenutku otkrovenje! Jednostavno sve ono preko cega sam se spoticao svih ovih godina savrseno se uklapalo, sve je bilo jasno :)
Neoboriva cinjenica je da nije dovoljna samo ljubav ucenika za ucenjem nego je potrebna i ljubav i zelja nastavnika profesora da pouci. Ako jedno od to dvoje omane - aj zdra'o! :)
Ja sam inace imao problema sa elektronikom, ali cvrsto sam odlucio da je shvatim i da radim nesto prakticno sa njom. Evo u mojoj biblioteci dva prirucnika od preko hiljadu stranica, jedan toolkit iz elektronike, sad samo cekam na onaj famozni klik' da se desi... i malo vremena :)
Ne znam koliko je nekom od vas pomoglo ovo sto sam napisao, ovo su neke moje misli i iskustva koje sam sazeo u jedan post, vise kao razmisljanje na glas.
Samo jos da kazem, ako nikada niste culi za Hilbertov tzv. 10. problem, odite na ovaj link i pogledajte ovih par dijelova ako budete imali vremena: http://www.youtube.com/results...query=Chaitin&search_type=
Ukratko, radi se o tome kako da se koncipira i realizuje jedan formalni sistem koji bi mogao svaku teoremu da verifikuje ili falsifikuje (to bi nam dosta posla ustedilo, sta vi kazete? :))))) Par ljudi u 20. vijeku su nasli rijesenje za 10.problem, a rijesenje je da rijesenja uopste nema! Zakljucak do kojih su dosli ti ljudi je da nijedan formalni sistem kombinovano sa svim znanjem koje je ikad nakupljeno kombinovano sa najvecim genijem u istoriji ne moze da rijesi sve probleme. Zakljucak do kojeg su dosli je da postoje problemi koje mi jednostavno ne mozemo logicki rijesiti. To ne znaci da su ti problemi previse slozeni sami po sebi, nego ih mi jednostavno ne mozemo rijesiti. Jedini nacin kako je moguce da ih rijesimo je INTUICIJA! :)
Veliki pozdrav svima i nemojte zamjeriti! [ Astek @ 13.05.2008. 21:07 ] @
1. Huemaj, svaka čast na postu. Sjajno.
2. Školski integrali i izvodi se uglavnom svode na šablonsko rešavanje zadataka. Imaš tablicu , nekoliko desetina tipskih smena i udri... Uglavnom se mogu rešiti. Za prosečnog đaka ili studenta neuporedivo je teže rešiti bilo koji zadatak koji počinje sa dokazati.. ma koliko lak bio. Preduslov za rešavanje takvih zadataka je odlično poznavanje i RAZUMEVANJE teorije i primena nekih već na predavanjima rađenih stavova, teorema, osobina,primera.. u rešavanju takvog zadatka. Zato je uvek bilo teže položiti algebru, teoriju algoritama, funkcionalnu analizu nego numeričku matematiku ili analizu I. Zamalo da zaboravim da pomenem geometriju. Ne kažem da je ovo uvek tačno ali to su moja subjektivna zapažanja iz perioda dok sam studirao.
3. Ne znam koga treba okriviti za ovakvo stanje u nastavi matematike(najpre u srednjim školama). Ministarstvo, profesore, đake ili roditelje. Ili sve nas zajedno. Mislim da je program za srednje škole preambiciozan, ma koliko mi Srbi bili "pametni". Moj dobar prijatelj radi u školi , i priča da on ne sme na pismenom ni da da neki zadatak koji nije rađen na času a kamoli nekakav dokaz ili teoriju. Pokušavao je pre par godina ali su se digli svi protiv njega a najviše roditelji i na moje iznenađenje kolege na poslu. Na kraju mu je došao i neki savetnik za matematiku i odustao je čovek.
[ petarm @ 14.05.2008. 07:47 ] @
Citat: Ojler: Slazem se sa Astekom da se u nasim skolama matematika shvata vise kao jedna vezba, dril a ne
kao jedna duhovna disciplina. Mnogi koji imaju dobre ocene iz srednje skole misle da znaju matematiku,
a veliki broj njih nije nikada ucio teoriju i dokaze. Vazno je resavanje zadataka, ali to nije jedino sto djaci treba da znaju.
To je isto kao sto neki znaju da sviraju, a ne znaju note. Nasi djaci su sluhisti.
Ne bih se slozio sa ovim. Sluhisti nisu nadrilovani. Vec rade neke stvari po osecaju. Za matematiku je to ogromna stvar! Nasi djaci uce note, ali nauce da sviraju samo odredjene kompozicije! [ Ojler @ 14.05.2008. 09:03 ] @
Možda nisam izabrao najsrećnije poređenje, ali poenta je ono o čemu i Astek piše.
Đaci uče šablonski zadatke, čak i oni koji imaju najbolje ocene. U tome je problem.
Pri tome đaci postaju teorijski nepismeni. Oni znaju neka pravila i neke formule, ali ne bi znali to da izvedu ili dokažu.
Zato sam to uporedio sa sluhistima koji su muzički nepismeni.
Uzmite npr. izvode i ispitivanje funkcije.
Znaju đaci izvode i da ispitaju funkciju, ali retko ko će vam znati da odgovori zašto se traži da je prvi izvod jednak baš nuli u traženju ekstremuma funkcije.
Još manji broj zna da objasni sam pojam izvoda pomoću limesa i onog malog trougla uz objašnjenje tangensa u tom trouglu da je to ustvari koeficijent pravca tangente itd.
Za ovo ne treba neka posebna nadarenost da bi se razumelo i objasnilo. Reč je o neznanju.
[Ovu poruku je menjao Ojler dana 14.05.2008. u 11:15 GMT+1]
[ MixMaster @ 16.05.2008. 20:14 ] @
Citat: Astek: Dakle svi mogu? Svaki prosečan srpski srednjoškolac može da recimo savlada Teoriju grupa sa svim onim silnim teoremama i dokazima? Možda je i tako . Ipak smo mi zemlja čuda.
P.S: Ja ipak tehniku integrala i diferencijala ne smatram vrhunskim dostignućem u matematici.
Jedan "prosjecan" srednjoskolac je "prosjecan" zbog razlicitih stvari...prije svega zbog sistema obrazovanja. Jedan od problema, recimo, je prevelik broj ucenika u odjeljenjima. U mojoj gimnaziji u prva dva razreda bilo nas je nesto manje od 20. To je bilo fino vrijeme. Em sto su profesori stizali da nas ispitaju relativno brzo, em smo se mi svi, medjusobno, solidno znali i lijepo druzili. Dakle, mozemo da izvedemo zakljucak iz ovoga koji bi glasio ovako: ako se broj ucenika povecava, znanje prosjecnog ucenika se smanjuje. Ili se ti mozda ne bi slozio sa mnom?
Da zakljucim, ako ucenik nije, daleko bilo, mentalno zaosto u razvoju (ne znam ljepsi naziv za ovo, a ne zelim da vrijedjam ovakve osobe), onda on moze da nauci i "teoriju grupa sa silnim teoremama i dokazima". Naravno, preduslov je da je on zainteresovan za to ili bar da ima nekoga da ga zainteresuje (najbolje je da se to radi dok je osoba mlada...ali ovo je vec druga prica).
Sto se tice integralnog i diferencijalnog racuna ja, za razliku od tebe, smatram da je to jedno fenomenalno otkrice, blago receno  [ Astek @ 17.05.2008. 13:12 ] @
Citat: MixMaster:Dakle, mozemo da izvedemo zakljucak iz ovoga koji bi glasio ovako: ako se broj ucenika povecava, znanje prosjecnog ucenika se smanjuje. Ili se ti mozda ne bi slozio sa mnom?
Ne bih se složio sa tobom. Isključujem ekstremne slučajeve gde u razredu ima preko 30 đaka. Uostalom , mi ovde pričamo o čoveku koji je upisao PMF (čini mi se) i ima određenih problema u savlađivanju tog gradiva.
Citat: MixMaster
Da zakljucim, ako ucenik nije, daleko bilo, mentalno zaosto u razvoju (ne znam ljepsi naziv za ovo, a ne zelim da vrijedjam ovakve osobe), onda on moze da nauci i "teoriju grupa sa silnim teoremama i dokazima". Naravno, preduslov je da je on zainteresovan za to ili bar da ima nekoga da ga zainteresuje (najbolje je da se to radi dok je osoba mlada...ali ovo je vec druga prica).
Uvek me je zbunjivala činjenica da većina naših ljudi lako prihvata činjenicu da nisu svi rođeni da bi bili odlični sportisti ali da se veoma ljute kada neko kaže da ni svi nisu rođeni da bi bili dobri matematičari. Prihvatimo činjenicu da postoje razne vrste inteligencije: verbalna, muzička, sportska... i ako sme da je pomenem racionalno-logička. Za školsku matematiku i većinu fakulteta dovoljan je solidan rad da bi se to savladalo. Za ozbiljnije stvari uz rad(kod nekih manji a kod nekih , bogami rudarski) ipak je neophodno imati malo smisla za to što se radi. Nemam tačne podatke, ali mislim da je na PMF prosek studiranja preko 8 god(onih koji završe) a da je ukupan broj svršenih studenama negde oko 10%. Zašto je to tako , to je posebna tema . Ja takođe mislim da se može mnogo štošta tu poboljšati od načina rada , broja studenata, njihovih obaveza, do korenitih promena u radu profesora i asistenata.
Citat: MixMaster
Sto se tice integralnog i diferencijalnog racuna ja, za razliku od tebe, smatram da je to jedno fenomenalno otkrice, blago receno :-)
Upšte ne govorimo o istoj stvari. Nisam komentarisao diferencijalni i integralni račun u smislu njihovog značaja u nauci već njihovu ulogu u školskim planovima. Očito si preskočio post moj predhodni post pa ga ponavljam:
Školski integrali i izvodi se uglavnom svode na šablonsko rešavanje zadataka. Imaš tablicu , nekoliko desetina tipskih smena i udri... Uglavnom se mogu rešiti. Za prosečnog đaka ili studenta neuporedivo je teže rešiti bilo koji zadatak koji počinje sa dokazati.. ma koliko lak bio. Preduslov za rešavanje takvih zadataka je odlično poznavanje i RAZUMEVANJE teorije i primena nekih već na predavanjima rađenih stavova, teorema, osobina,primera.. u rešavanju takvog zadatka. Zato je uvek bilo teže položiti algebru, teoriju algoritama, funkcionalnu analizu nego numeričku matematiku ili analizu I. Zamalo da zaboravim da pomenem geometriju. Ne kažem da je ovo uvek tačno ali to su moja subjektivna zapažanja iz perioda dok sam studirao.
Još nešto: ako neko jako mnogo radi , a stigao je do fakulteta, i teško može da ponovi dokaz već poznate teoreme možda je vreme da razmisli o izboru fakulteta(ili pak smera na istom). Neće mu pomoći opservacije tipa : samo ti radi doći će sve na svoje mesto, bitno je biti uporam...
[ MixMaster @ 19.05.2008. 09:55 ] @
Ne brini se, nisam preskocio ni jedan post, cak sam detaljno sve procitao. Mislim da je tvoj prvi odgovor meni bio:
Citat: Astek: Dakle svi mogu? Svaki prosečan srpski srednjoškolac može da recimo savlada Teoriju grupa sa svim onim silnim teoremama i dokazima? Možda je i tako . Ipak smo mi zemlja čuda.
P.S: Ja ipak tehniku integrala i diferencijala ne smatram vrhunskim dostignućem u matematici.
...pa sam ti zato, izmedju ostalog, odgovorio sa:
Citat: Sto se tice integralnog i diferencijalnog racuna ja, za razliku od tebe, smatram da je to jedno fenomenalno otkrice, blago receno :-)
Totalno druga stvar je, nacin ucenja, koji ti kritikujes u:
Citat:
Školski integrali i izvodi se uglavnom svode na šablonsko rešavanje zadataka. Imaš tablicu , nekoliko desetina tipskih smena i udri... Uglavnom se mogu rešiti. Za prosečnog đaka ili studenta neuporedivo je teže rešiti bilo koji zadatak koji počinje sa dokazati.. ma koliko lak bio. Preduslov za rešavanje takvih zadataka je odlično poznavanje i RAZUMEVANJE teorije i primena nekih već na predavanjima rađenih stavova, teorema, osobina,primera.. u rešavanju takvog zadatka. Zato je uvek bilo teže položiti algebru, teoriju algoritama, funkcionalnu analizu nego numeričku matematiku ili analizu I. Zamalo da zaboravim da pomenem geometriju. Ne kažem da je ovo uvek tačno ali to su moja subjektivna zapažanja iz perioda dok sam studirao.
...sa cime bih se ja, slozio.
Mislim da bi se to stanje jedino promijenilo kada bi smo svi nekako saradjivali...tacnije, kada bi smo izvukli neke zakljucke iz naseg razgovora na ovim forumima, i kada bi to mogli da posaljemo nadleznom ministarstvu. Nisam primijetio da se ista promijenilo u zadnjih, 15tak godina i ako je bilo nekih "reformi" i slicno... Dok god profesori u osnovnim i srednjim skolama budu predavali gradivo na nacin na koji se ista predaje i na fakultetu ili dok god na ETF-u budu predavali matematiku na nacin na koji je predaju i na PMF-u (iliti MATF-u) ili...
Sto Ojler rece:
Citat:
Još manji broj zna da objasni sam pojam izvoda pomoću limesa i onog malog trougla uz objašnjenje tangensa u tom trouglu da je to ustvari koeficijent pravca tangente itd.
Dakle, za odredjene grupe ljudi moraju postojati odredjeni nacini objasnjenja iliti "prilaza" materiji.
Toliko za sada... [ miki069 @ 20.05.2008. 22:47 ] @
Kakvo smaranje sa matematikom na tehnickim fakultetima? Matematika u prvoj godini na svim tehnickim fakultetima je nivoa gimnazijske matematike. Oduvek bilo tako. Sad po Bolonji? Podeljeno na semestre, u svakom semestru po n kolokvijuma i n^2 popravnih kolokvijuma. Ajde neko ko je smoren matematikom nek okaci zadatke sa kolokvijuma (I, II, III ili n-tog) pa da se javi masa gimnazijalaca koja ce uraditi sve zadatke za 20 minuta. Ja za 10 minuta sa pisanjem. Moze i sa objedinjenog semestralnog "pismenog" ispita. To je ispod novoa srednje skole. Smesno.
Znate na kom "tehnickom" fakultetu je najteza matematika u zadnjih 5 godina? Na Ekonomskom. Ako ne verujete kacim zadatke. Zadnijih 15 godina je opadao nivo matematike na tehnickim fakultetima i dosao je ispod gimnazijskog nivoa. Toliko o smaranju sa matematikom na tehnickim fakultetima.
Cast izuzecima kao sto su Elektronski i Gradjevinski fakultet u Nisu. Bar bilo do prosle godine, do uvodjenja Bolonje.
[ MixMaster @ 20.05.2008. 23:12 ] @
Miki, ne znam sta da ti kazem  Dakle, ti si bio na svim ostalim tehnickim i "tehnickim" fakultetima, u svim gradovima Srbije(?) izgleda? Bio si i na starom sistemu i na Bolonji? Dobro, moram da stanem da i ja ne krenem da pricam svasta 
Dakle, ponovicu jos jednom sledece:
Citat: Dok god profesori u osnovnim i srednjim skolama budu predavali gradivo na nacin na koji se ista predaje i na fakultetu ili dok god na ETF-u budu predavali matematiku na nacin na koji je predaju i na PMF-u (iliti MATF-u) ili...
...a razlog za receno, se moze prepoznati u:
Citat:
Dakle, za odredjene grupe ljudi moraju postojati odredjeni nacini objasnjenja iliti "prilaza" materiji.
Po treci put...iliti da zakljucim: nije problem u kvantitetu, vec u kvalitetu 
Pozdrav. [ Ojler @ 21.05.2008. 08:32 ] @
Ovo mi je nov podatak da je matematika na tehnickim fakultetima boza.
Ako je to tacno, onda je nase obrazovanje konacno propalo.
Imacemo inzenjere koji nisu mnogo odmakli od majstora.
Nekad se ozbiljno radilo na ETF-u, Masinstvu, Gradjevini u Beogradu.
[ Astek @ 21.05.2008. 09:03 ] @
Citat: miki069: Ako ne verujete kacim zadatke.
Okači. PMF(analizu ili linearnu algebru iz I godine), ETF i Ekonomski.
Davno sam završio PMF, u međuvremenu se nisam više bavio matematikom pa me interesuje šta se u međuvremenu promenilo.
Inače se slažem sa Ojlerom.
[ boolander @ 21.05.2008. 11:00 ] @
ja još uvek studiram na MATF-u i malo toga se promenilo od kako se prešlo na bolonju... većinom je sve podeljeno na dva semestra uz neznatno skraćenje gradiva, a to skraćenje je u vidu da se ne radi baš sve do u sitna crevca nego one bitnije stvari se rade malo ozbiljnije... što se tiče analize i linearne algebre tu se ništa bitno nije promenilo analiza1 je ista i sluša se u prvom i drugom semestru, isto je i sa linearnom algebrom samo što se sluša u drugom i trećem semestru, a polažu se deo po deo a ne kao pre celo gradivo
[ miki069 @ 21.05.2008. 20:26 ] @
Masinski fakultet
Matematika I
k-ti kolokvijum po redu (ne znam koji), al tema kolokvijuma su funkcije.
1. zadatak:
"Detaljno ispitaj i precizno nacrtaj grafik funkcije y=(- x^2 + 6*x - 9)/(x-2)"
2. Zadatak:
a) "Funkciju y=kvadratni koren(2*x + 1) razviti u MekLoranov polinom treceg stepena"
b) "Koristeci dobijeni razvoj izracunaj pribliznu vrednost kvadratnog korena(3)"
Vreme izrade zadataka 120 minuta
Ekonomski fakultet
Matematika I
k-ti kolokvijum po redu (ne znam koji), al tema kolokvijuma su funkcije.
1. zadatak:
"Odredi domen, intervale monotonosti i ekstremne vrednosti funkcije y=ln((3-x^2)/(x+2))"
2. Zadatak:
"Odredi domen, intervale konkavnosti i konveksnosti i PT funkcije y = x^2*e^(1/x)
3. Zadatak:
"Detaljno ispitaj i nacrtaj grafik funkcije y=(lnx)^3 + (lnx)^2 - 2*lnx"
4. Zadatak:
"Data je funkcija traznje x=-(2/3)*p + 120 i funkcija ukupnih troskova C = X^2 + 200. Odrediti:
a) karakteristicnu traznju i cenu
b) maximalan ukupni prihod
c) intervale rentabilnosti
d) maksimalnu dobit
e) elsticnost funkcije traznje u normalnom i inverznom obliku
f) u istom koordinatnom sistemu skicirati grafike funkcija: ukupnog prihoda, troskova i dobiti"
Vreme izrade zadataka 120 minuta.
Nije na Ekonomskom toliko teze al je mnogooo glomaznije za isto vreme.
Kod MekLoranovog polinoma se ne trazi procene greske. U moje vreme se trazila.
Sve funkcije koje su date su tamo gde su i neprekidne ujedno i diferencijabilne. Nema "siljaka" na graficima. U moje vreme je bilo nezamislivo dobiti na ispitu zadatak bez bar jednog "siljka".
Sve nule funkcija i svih izvoda se odredjuju lako, bez pribliznih metoda, sto je isto u moje vreme bilo nezamislivo.
Funkcija ide uvek glatko, nikad ne predje preko HA ili KA, sto se smatra mnogo laganim i moje vreme je bilo nezamislivo.
KA je jednoznacna na obe strane sto je opet mnogo lako.
itd..
PMF (matematika) ne smatram za tehnicki fakultet. Mada je sad i tamo labavo. Na hemiji i fizici pogotovo.
Da kacim kolokvijume iz integrala. Smejacete se. Zeza me ovaj TEX. Ne znam da pisem u njemu.
[ Astek @ 21.05.2008. 23:32 ] @
Zbunjuju me malo ovi zadaci sa Ekonomskog. Ne čini mi se da su sva četiri sa istog ispita. Prva tri su koliko mogu da procenim Matematika sa prve godine ali četvrti mi više liči na nešto kao Matematičko modeliranje (ili kako se već zvao ranije taj ispit) sa mislim druge godine. Da nisu spojili ta dva ispita u jedan?
Da su laki jesu, pogotovo sa mašinskog. Ali i kad sam ja studirao mašinski i građevinski su imali za klasu lakše zadatke od recimo ETF-a.
[ MixMaster @ 22.05.2008. 19:58 ] @
Pa miki069, sta je problem? Kazu ti ljudi, i evo ja cu jos jednom, da su neki ispiti podijeljeni. Ne brini, radi se isto sto se radilo i dok si ti bio na faksu. Ovo znam iz iskustva, jer mi radimo iz starih knjiga. Inace, mogu ti reci da sam se oprobao i na starom i na novom sistemu. Nije za pohvalu, ali, sta da se radi... Stari sistem je imao jednu prednost a to je veliki broj rokova. Prednosti koje su bile planirane, donosenjem novog sistema, kompenzovane su jednim ispitnim rokom (+popravni), tako da ne bih rekao da su mnogo toga napravili. O nacinu predavanja i praksi, ni rijeci...vec samo "skrati ovo, produzi ono...".
Nase obrazovanje se stalno vrti u krug. Vazniji su nam neki "standardi" nego kvalitet, koji moze da se stvori jednostavno, ali o tome mozete procitati u jednom od mojih prethodnih poruka.
Pozdrav.
[ miki069 @ 22.05.2008. 23:33 ] @
U pravu si MixMaster.
Pozdrav
[ Burgos @ 11.02.2009. 15:40 ] @
Zaista mi je žao što čupam ovu temu iz karantina, ali da repliciram na post:
Citat: miki069: Kakvo smaranje sa matematikom na tehnickim fakultetima? Matematika u prvoj godini na svim tehnickim fakultetima je nivoa gimnazijske matematike. Oduvek bilo tako. Sad po Bolonji? Podeljeno na semestre, u svakom semestru po n kolokvijuma i n^2 popravnih kolokvijuma. Ajde neko ko je smoren matematikom nek okaci zadatke sa kolokvijuma (I, II, III ili n-tog) pa da se javi masa gimnazijalaca koja ce uraditi sve zadatke za 20 minuta. Ja za 10 minuta sa pisanjem. Moze i sa objedinjenog semestralnog "pismenog" ispita. To je ispod novoa srednje skole. Smesno.
Znate na kom "tehnickom" fakultetu je najteza matematika u zadnjih 5 godina? Na Ekonomskom. Ako ne verujete kacim zadatke. Zadnijih 15 godina je opadao nivo matematike na tehnickim fakultetima i dosao je ispod gimnazijskog nivoa. Toliko o smaranju sa matematikom na tehnickim fakultetima.
Cast izuzecima kao sto su Elektronski i Gradjevinski fakultet u Nisu. Bar bilo do prosle godine, do uvodjenja Bolonje.
Nadoknadivi kolokvijumi? Čekaj... Nadoknadivi kolokvijumi? Kakvi crni nadoknadivi kolokvijumi..?! :(. Prvo, Bolonja je, po mom mišljenju, zaista nakaradno primenjena u Srbiji (teško da je moguće primeniti Bolonjsku konvenciju na fakultetu gde se 500+ ljudi guši u amfiteatru koji je do te mere krcat da asistent ne može da siđe sa katedre, čak ni na pauzi). n kolokvijuma? Pa, na ETF su tradicionalno organizuje isključivo jedan nenadoknadivi kolokvijum koji nosi trideset procenata od ukupnog broja poena (što bi rekli, predispitne aktivnosti :) ).
Što se tiče zadataka, par uzoraka se mogu naći na matematika.etf.rs . Ako bi ih masa gimnazijalaca rešila, to može samo da znači da sam ja završio pogrešnu gimnaziju.
Ne mislite da sam isfrustriran matematikom (izgleda da sam je, konačno, položio :) ), ali stvari nisu baš kao u postu iznad.
[ Mikky @ 11.02.2009. 19:21 ] @
Naravno da nisu stvari kao u postu iznad... Matematika na fakultetu (1. god bilo kog tehnickog) je daleko iznad matematike u gimnaziji (ne racunam matematicke gimnazije) i svaka izjava koja kaze obrnuto je u najmanju ruku neozbiljna.
Ipak tacno je da su kriterijumi danas dosta nizi nego pre 20ak godina i mislim da mnoge starije generacije bas to "boli". U neku ruku ih razumem jer je normalna reakcija to da su oni za istu diplomu ulozili mnogo vise truda nego danasnje generacije. Ali na kraju se sve opet svede na to da koliko znas toliko ces kasnije i moci da to iskoristis. Drugim recima vaznije je znanje od diplome, pa prema tome mislim da nema mesta toj ogorcenosti.
[ miki069 @ 17.02.2009. 10:01 ] @
Evo primera tog integralnog ispita sa ETF (najteža vrsta pismenog ispita - koliko sam ja skontao):
glavni deo ispita (u trajanju od 150 minuta):
1. Ispitati da li je operacija * definisana sa x*y = x + 4xy + y unutrašnja operacija na skupu Q \ (-0.25).
2. Dve smešno lake determinante......
3. Smešno laka deljivost polinoma.
4. 2 smešno laka limesa
5. jedan težak i jedan lak limes..
6. Detaljno ispitati tok i nacrtati grafik funkcije f(x) = x^2 * ln(ABS(x))
Za ovakvih 5 zadačića gimnazijalci imaju na pismenom vreme od dva školska časa ili ti svega 90 minuta.
Ovde na ETF je vreme za ovih 6 zadačića 150 minuta.
Uostalom neka se gimnazijalci izjasne sami.
Moji (sa ocenama 4 i 5) bi svi položili ovaj pismeni sa ETF-a sa najmanje osmicama, devetkama a bilo bi i desetki.
[ ptak 13. @ 19.02.2009. 22:09 ] @
Matematiku ma kakava bila ne trebas bubati i uciti, matematika se vezba i vezbom se radi najbolje....sve je na neki nacin sablon....bar po meni samo je vezbanje bitno ! ! !
[ Nemanjich @ 20.02.2009. 07:41 ] @
Za miki069 , ja studiram etf ,ti si ovde dao samo trecinu jednog ispita, fali jos dosta teorije i ispit pre ispta(koji mora da se polozi da bi se uopste drugi deo ispita pregledao, radi se pola sata 10 zadataka, 6 apsolutno tacnih(zarez da fali ne priznaje se) da bi se proslo, glavni problem je poloziti ovaj deo, 90 posto ljudi padne ovde). Ako je sve to tako lepo prosto da ne poverujes, kako onda od skoro 1000 ljudi ispit je polozilo samo 70(ja sam je polozio,ali u februaru, nisam uradio taj prvi deo u januaru)?
taj ispit sto si ti naveo nije uopste toliko tezak kakvih ima mozes ih naci na matematika.etf.rs. I nemojte sad o tome kako je etf ultra lak fakultet, studirajte ga pa ce te viditi.
ima jos stvari zbog cega je tesko ali da ne sirim temu....
[Ovu poruku je menjao Nemanjich dana 20.02.2009. u 15:27 GMT+1]
[ kingakul @ 02.04.2009. 11:36 ] @
Da ocena da su rokovi sa ETF-a "laki" ili "laksi od kontrolnih zadataka u gimnazijama" je data krajnje pausalno. Tacno je da su laksi od matematicke gimnazije, ali to je sve. Evo primer jednog roka (FEB 08) iz M1: http://matematika.etf.rs/predm...08_parcijalni_ispit_zadaci.rtf
Pogledajte samo 1. zadatak i prostor koji je ostavljen da se uradi i broj poena za isti. A ovo je kao sto je kolega rekao pola ispita (deo sa zadacima i nosi 50% a ispit se ukupno radi 150min - a ne samo ovaj deo), pre cega se mora poloziti ulazni test, a postoji i teorijski deo posle. [ Nedeljko @ 02.04.2009. 13:57 ] @
Ovaj rok je smešan. Mogu da ga uradim za 15 minuta. Koliko vidim, dato je deset puta više vremena. Ovo bi imalo smisla za ispit koji se radi do 60 minuta.
[ kingakul @ 02.04.2009. 18:23 ] @
Zanimljivo da to znate da uradite za 15min, a da ne znate da mnozite ili mozda niste pazljivo procitali sta sam napisao.
Edit: U svakom slucaju ne razumem potrebu za tim hvalisanjem. Ko ste Vi uopste? Student I godine na tehnickom fakultetu ili sa neke druge pozicije tvrdite da mozete to da uradite za 15min?
[ Nedeljko @ 03.04.2009. 08:00 ] @
Nebitno je ko sam. Mogu da uradim za 15 minuta, jer odmah znam šta i kako treba da radim. Čim pogledam zadatak, znam kako se rešava. No, studentu treba malo vremena za lutanje, isprobavanje raznih varijanti, proveru itd. Da sam u malo boljoj kondiciji, uradio bih za 10-tak minuta, što znači da bi taj test trebalo raditi 45 minuta. Smatram da je studentu treba dati 4x više vremena nego što je potrebno za pravolinijsko rešavanje (žmureći).
[ miki069 @ 03.04.2009. 09:39 ] @
Svi zadaci osim 3. su iz srednjoškolskih zbirki za IV godinu - uglavnom Vene.
Oni za takvih 5 zadataka dobijaju na pismenom 90minuta.
Nedeljko je u pravu da studentima ne treba dati više od 60 minuta za ove zadatke.
Ja sam za 30 minuta uradio za maximalnih 100%. Za 25 minuta sam imao jednu grešku. A nisam u nekoj formi za rešavanje zadataka. Ko vežba baš kao što kaže "pravolinijski" svodi se samo na vreme potrebno za pisanje.
Nađite neki rok od pre 10-ak godina sa ETF-a, tehnološkog, građevine... u Beogradu ili elektronskog u Nišu pa vidite.
To je bila fakultetska matematika. Da ne spominjem smerove matematika-informatika na PMF-u. Oni su bili i ostali profesionalci.
Ovo sad na tehničkim fakultetima je Bolonjska = srednjoškolska matematika.
[ kingakul @ 03.04.2009. 09:44 ] @
Dakle asistent na gradjevinskom fakultetu iz matematike. Pa Vama je posao da resavate te zadatke i prosli ste ih mali milion puta i ne vidim zasto je onda to veliki uspeh sto mozete da resite za 15min. Studenti koji to resavaju se skoluju da grade mostove npr. a ne da pisu zbirke zadataka iz matematike.
U svakom slucaju u poziciji ste da iste nadjete pa kacite vi te rokove od pre 10 godina da vidimo tacno koliko je sada smesno, a koliko je onda bilo komplikovano.
[ Nedeljko @ 03.04.2009. 10:38 ] @
Nisam ninakakvom fakultetu, ali nije bitno. Bitno je da student dobije 4x više vremena nego što treba pravolinijski.
No, da se ispravim. Zadaci i ne treba da budu teški. Problem je ako se zavaljuju kao neke zadačine, a na ispitu se prepisuje. Bolje je da zadaci budu nalik ovim, ali da onaj ko je to položio to zaista i zna. Kad bolje razmislim, šta će elektroinženjeru teži zadaci iz ovih oblasti.
[ Nedeljko @ 03.04.2009. 10:43 ] @
Evo jednog zadatka sa psimenog ispita iz C-a na ETF-u, od pre oko 15 godina:
Na ulazu je dat prirodan broj n. Podeliti skup prirodnih brojeva od 1 do n2 na n disjunktnih podskupova sa po n elemenata tako da zbir elemenata svakog od tih podskupova bude isti.
[ kingakul @ 03.04.2009. 11:31 ] @
Vi mislite da zadaci iz C-a bi trebalo da budu magicni kvadrati nXn?
[ miki069 @ 03.04.2009. 11:41 ] @
Nije magični kvadrat.
n-disjunktnih podskupova jednakog zbira je drugačiji zahtev.
Kod magičnog kvadrata nisu uvek disjunktni jer se gledaju i horizontalni i vertikalni zbirovi.
Zadatak je logičke prirode i nije vezan za kodiranje u C jeziku.
Može se iskodirati posle i u Delphi-ju, VB-u... ko šta voli i zna
[ kingakul @ 03.04.2009. 11:48 ] @
Ha ha pa naravno da jesu i kod magicnog kvadrata disjuktni ako znas da izvuces to sto ti treba iz njega.
Edit: zadatak je bezveze! Ne ulazeci u to da li je tezak/lak on nicemu ne sluzi i iz njega se moze vrlo malo nauciti vezano za predmet.
[ miki069 @ 03.04.2009. 12:02 ] @
Magični kvadrat nema n disjunktnih podskupova sa po n elemenata, već najmanje 2n (n po H i n po V) nedisjunktnih poskupova.
Ako se gledaju i dijagonale onda još više od 2n.
Teži je uslov od ovog zadatka.
Jasno da iz magičnog kvadrata sledi rešenje ovog zadatka. Obrnuto ne važi.
Ovo je vezano za metode (principe) programiranja a ne za programski jezik C.
Rešavanjem ovakvih zadataka se uči programiranje nevezano za jezik u kome će se iskodirati.
[ kingakul @ 03.04.2009. 12:08 ] @
"Magični kvadrat nema n disjunktnih podskupova sa po n elemenata, već najmanje 2n (n po H i n po V) nedisjunktnih poskupova. "
Ja stvarno ne razumem ovu recenicu? Kako ovo prvo iskljucuje ovo drugo?
Iz resenja ovog zadatka sledi magican kvadrat uz malo inzenjerske intuicije. Obrnuto ne vazi ne mogu se iz magicnog kvadrata iskonstruisati sva resenja ovog zadatka.
[ miki069 @ 03.04.2009. 12:12 ] @
Ne isključuje ga već je samo potreban uslov ali ne i dovoljan da bi bio magični kvadrat.
Gde su tražene sve podele na po n disjunktnih podskupova? Na osnovu čega tvrdiš da ih ima više od jedne? Ili bar jedna?
Odakle to da je magični kvadrat jedinstven? Što ako ih više od jednog? Ili nema ni jedan?
I za jedno i drugo odmah izbacujem program u Delphi-ju samo da preuredim moj moćni generator kombinacija.
Al šta je tu sporno? Dokaz egzistencije bar jednog rešenja. Da je za svako n moguća podela zbog traženog uslova da zbir bude isti.
Ja ću dokazati ispravnost programa - načina traženja rešenja. Ali to ne garantuje da za svako n postoji rešenje.
Možda za n=13 nema ni jedne podele a kamo li magičnog kvadrata.
[Ovu poruku je menjao miki069 dana 03.04.2009. u 13:36 GMT+1]
[ Nedeljko @ 03.04.2009. 14:38 ] @
Skup od n 2 elemenata ne može imati više od n disjunktnih podskupova. No, magični kvadrat ima 2n+2 uslova, a ovaj zadatak n, pa nije sasvim isto. Ovo je uslov samo za vrste magičnog kvadrata.
Citat: kingakul: Vi mislite da zadaci iz C-a bi trebalo da budu magicni kvadrati nXn?
Ne, samo mislim da ima budala na unizveritetu, a ovo nije anegdota, već gola istina!. Jedan moj drug tada polgao pismeni iz C-a na ETF-u i imao je taj zadatak. Mogu da obesim rešenje. Nakucao sam ga za okruglo 10 minuta, iskompajlirao iz prve i odmah je proradio šta treba. Zabezeknut sam, jer mi ni samo kucanje skoro nikad ne prolazi bez sintaksnih grešaka. [ kingakul @ 03.04.2009. 15:42 ] @
Pa ajde okacite resenja da vidimo cije je bolje.
[ Nedeljko @ 03.04.2009. 15:51 ] @
Ovo je program napisan po ideji mog drugara, koji se ovoga setio na pismenom, ali nije umeo da iskodira.
Code:
#include <stdio.h>
#include <stdlib.h>
int main() {
int n = -1;
int i, j;
while(n <= 0) {
printf("Unesite prirodan broj:\n");
scanf("%d", &n);
if (n <= 0) {
printf("Uneseni broj nije prirodan\n");
}
}
printf("Skup {1,...,%d} se moze podeliti na %d disjunktnih podskupova"
" sa po %d elemenata tako da zbir elemenata svakog od njih bude isti na sledeci nachin:\n", n*n, n, n);
for (i = 0; i < n; ++i) {
printf("{");
for (j = 0; j < n; ++j) {
printf("%d", j*n+(i+j)%n+1);
if (j < n-1) {
printf(",");
}
}
printf("}");
if (i < n-1) {
printf(",");
}
printf("\n");
}
return EXIT_SUCCESS;
}
[ Nedeljko @ 03.04.2009. 15:56 ] @
Magični kvadrat neparnog reda bi se dobio ako bi se formula n+(i+j)%n+1 zamenila formulom n+2*(i+j)%n+1. Magični kvadrati parnog reda različitog od 2 se konstruišu drugačije. Postoji posebna konstrukcija za red deljiv sa 4 i za paran red različit od 2, koji nije deljiv sa 4.
[ ksrele @ 03.04.2009. 16:16 ] @
Procitao sam celu temu pazljivo i detaljno (jedino mozda nisam bas vodio racuna ko je sta pisao ali tematika me je vise zanimala).
Pre svega svaka cast Mikky-ju na ovoj temi. Neko je rekao da je bas njega opisao u pocetnoj poruci i ja bih to isto mogao da kazem.
Ja sada zelim da prekinem prepucavanje oko ovog zadatka koji, vidim, resavate u programskim jezicima.
Kod mene na Visokoj Tehnickoj Skoli u Subotici na casu matematike i na ispitima iz matematike NEMA RACUNARA!!! Osim na Numerickoj matematici (Matematika II ili III ne znam kako ide kod ETF-ovaca) gde se uci i ispituje rad u Mathlab-u ali i to je JAKO JAKO JAKO povrsno i traje pola semestra ako se dobro secam.
Da naglasim, ja sam student (apsolvent) Visoke Tehnicke Skole u Subotici i pisacu samo po ugledu na nju!
Upisao sam 2003 godine po kvazi-beta-bolonjskom sistemu?!?!? (ne bitno)
Za svaku matematiku smo imali po JEDAN semestar!!!
Imali smo:
1. Diskretnu matematiku (matrice, geometrija i slicno)
2. Analizu (izvodi, integrali, funkcije...)
3. Numericku matematiku (numericki redovi, parcijalni izovdi, numericke metode...)
Pored ovoga, imali smo brdo obaveza iz drugih predmeta (* na kraju poruke) koje smo MORALI da resimo da bi mogli da izadjemo na ispit. Mnogi studenti su morali birati sta ce prvo da rese jer je skoro nemoguce resiti sve odjednom. Vecina je izabrala da rade matematike prvo a ostale ispite da rade kad stignu pa su se zeznluli jer su profesori poludeli zasto oni nisu uradili OBAVEZNE kolokvijume a pokusavaju da izadju na ispite!
Ja sam izabrao da resim strucne i neke manje strucne ispite prvo pa onda matematike. Naravno, ja sam slusao predavanja i vezbe iz matematika ali nisam imao vremena za vezbanje.
E onda je dosao zanimljiv trenutak. Dosao neki predmet (digitalna obrada signala, valjda) gde smo koristili integral. OPA! Citiram profesora: "E ovde se koristi integral ali to necemo obradjivati jer to znate iz matematike"! Na zalost NIKO nije znao sta to profesor pise po tabli!!! Cak ni oni koju su polozili matematiku!!!
ZASTO niko nije znao o cemu se radi i ZASTO profesor nije hteo da nam objasni o cemu se radi???
Ja imam predlog za tehnicke fakultete za resenje ovog problema.
Prvo, da postoji NEOBAVEZAN predmet "Opsta matematika" gde se studenti upoznavaju sta sve moze da se radi u matematici ali ne i kako se to sve radi, osim naravno nekih najosnovnijih operacija.
E onda kada dodje neki strucni predmet i kada dodje deo gradiva gde se koristi, Furijev red recimo, da se pozove profesor matematike da lepo "gostuje" na casu i da objasni kako se koristi ta MATEMATICKA METODA u KONKRETNOM slucaju!!!
_______
*
ukupan broj predmeta: 47
broj predmeta po godinama: 15 + 16 + 16
skoro svaki strucni predmet je zahtevao odradjen kolokvijum (ili neki rad) pre izlaska na ispit.
[ kingakul @ 03.04.2009. 18:13 ] @
@Nedeljko: program nije tacan.
Ups izvinjavam se moja greska, zaboravio sam sta bi trebalo da radi.
Samo ne vidim kako ovo funkcionise:
" Magični kvadrat neparnog reda bi se dobio ako bi se formula n+(i+j)%n+1 zamenila formulom n+2*(i+j)%n+1. "
[Ovu poruku je menjao kingakul dana 03.04.2009. u 19:24 GMT+1]
[ Nedeljko @ 03.04.2009. 19:23 ] @
Treba n+(i+2*j)%n+1.
[ kingakul @ 03.04.2009. 19:33 ] @
To ponavlja brojeve u magicnom kvadratu.
Mislim nije ni bitno da se resi. Ko hoce moze da implementira ovo: http://en.wikipedia.org/wiki/Siamese_method
U svakom slucaju ovo nije nesto sto bi trebalo da se radi na ispitu iz C-a na ETF-u. Skrenuli smo sa teme uzgred.
[Ovu poruku je menjao kingakul dana 03.04.2009. u 20:49 GMT+1][ bezicnabubica @ 03.04.2009. 23:11 ] @
Nadjes dobrog matematicara i iznajmis bubicu. =_
[ kingakul @ 04.04.2009. 00:01 ] @
Nadjes dobrog elektroinzenjera i napravis ometac.
[ ptak 13. @ 04.04.2009. 08:23 ] @
U ala ste skrenuli sa teme  ajmo malo nazad
Citat: kingakul: Nadjes dobrog elektroinzenjera i napravis ometac.
kakav ometac  ? ne razumem bas ovu poruku u celoj temi  
I opet kazem, matematika se ne uci, nije to istorija, matematika se vezba i vezbom dovodi do savrsenstva....samo vezbanje ! ! ! i ugasite TV, komp, radio, DVD player, lap top, MP3, MP4 i ostale zajebancije kad vezbate matematiku.... [ ksrele @ 04.04.2009. 10:19 ] @
Citat: ptak 13.:
ugasite TV, komp, radio, DVD player, lap top, MP3, MP4 i ostale zajebancije kad vezbate matematiku....
E vidis, ja sam jedno vreme mnogo bolje uvezbavao matematiku, tacnije radio domaci u osnovnoj skoli, ako mi je pri tom vezbanju radila omiljena muzika.
Mnogi ce ti ovo potvrditi. E sadm sta naucnici kazu u vezi sa ovim ne znam, mada cisto sumnjam da se slazu da je to zaista dobra praksa, ali ako bas gledamo prakticno mnogima to pomaze. [ Srđan Pavlović @ 04.04.2009. 12:45 ] @
Hm, evo pokusacu da dam neko objasnjenje.
Misao i emocije su povezani. Kada kazem misao, ovde mislim u uzem smislu na koncentraciju za obavljanje
misaonih operacija (logicko rasudjivanje, mentalne operacije). Muzika utice na emocije.
Misli su neodvojive od emocija, prozete emocijama, kao i svaki nas pokret.
Povezani su u tom smislu sto emotivno stanje
moze bitno da utice na kvalitet ovih procesa (sposobnosti). Jedno objasnjenje moze biti da neka muzika deluje
pozitivno na emotivno stanje neke osobe, i samim tim cini je spremnijom da se kvalitetnije posveti radu.
Mozak ima sposobnost simulatne obrade informacija, kao i sekvencijalne. Tako da muzika uopste ne mora
biti ometajuci faktor dok se bavimo nekom misaonom aktivnoscu, naprotiv, moze je pospesiti, uticuci na
druge aspekte (emotivne) - dok se bavimo misaonom aktivnoscu (logickim rasudjivanjem, mentalnim ogledima, itd)
Recimo, kada igram CS, primetio sam da bolje igram uz GoaTrance tehno ;) verovatno podize malo
dodatno adrenalin i samim tim ubrzava reakcije organizma (brze primetim lika, brze stavim nisan na glavu,
brze kliknem...) i slicno ;)
Uostalom, ako vam je prijatnije da matematicke zadatke resavate uz muziku, i bolje ih resavate tako,
onda to i radite - manje je bitno zasto je to tako ;)
[ Nedeljko @ 05.04.2009. 14:48 ] @
Citat: ptak 13.: I opet kazem, matematika se ne uci, nije to istorija, matematika se vezba i vezbom dovodi do savrsenstva....samo vezbanje ! ! ! i ugasite TV, komp, radio, DVD player, lap top, MP3, MP4 i ostale zajebancije kad vezbate matematiku....
Moja iskustva su drugačija. Za matematiku su ključne teorija i njeno kvalitetno razumevanje. Onda se zadaci mogu čisto pogledati radi reda, a i ne moraju. Pismeni bi trebao da može da se položi sa ocenom najmanje 8 ako se zna teorija kako treba - bez ijednog urađenog zadatka. U teoriji piše sve šta treba za zadatke. Zadaci ne bi smeli da izlaze iz okvira pokrivenih teorijom. Sa druge strane, znam brdo ljudi koji su polagali pismene (bez nedozvoljenih sredstava i metoda), samo vežbajući zadatke, bez da su pogledali teoriju. Ni dan danas mi nije jasno kako to može. [ GoranM @ 21.04.2009. 05:51 ] @
Citat: Nedeljko: Moja iskustva su drugačija. Za matematiku su ključne teorija i njeno kvalitetno razumevanje. Onda se zadaci mogu čisto pogledati radi reda, a i ne moraju. Pismeni bi trebao da može da se položi sa ocenom najmanje 8 ako se zna teorija kako treba - bez ijednog urađenog zadatka. U teoriji piše sve šta treba za zadatke. Zadaci ne bi smeli da izlaze iz okvira pokrivenih teorijom. Sa druge strane, znam brdo ljudi koji su polagali pismene (bez nedozvoljenih sredstava i metoda), samo vežbajući zadatke, bez da su pogledali teoriju. Ni dan danas mi nije jasno kako to može.
Hmmm, bas bih voleo da vidim nekoga da je polozio pismeni ispit iz matematike koji se sastoji od zadataka, a da prethodno nije vezbao zadatke.
To je isto kao da neko uzme knjigu o karateu na primer, ili nekoj drugoj borilackoj vestini i procita je od korica do korica, "sa razumevanjem"
i onda kaze ja znam karate :-D
Matematika je slicna sportu, zahteva trening. Znaci da bi se dobro naucila matematika, treba vezbati do iznemoglosti. Naravno, teorija je isto tako vazna ali nista bez vezbe. Takodje, mislim da je jedan od vaznijih ciljeva matematike na fakultetu da istrenira studente da razmisljaju, budu sistematicni, i sto je najvaznije da budu uporni. Ono sto se zapocne, da se dovede do kraja (resi zadatak). To je kasnije veoma korisno cime god covek da se bavi, cak i ako zaboravi 90% onoga sto je naucio iz matematike. E i ovo je jos jedan razlog zasto je vezba neophodna.
[Ovu poruku je menjao GoranM dana 21.04.2009. u 07:26 GMT+1][ Nedeljko @ 21.04.2009. 10:39 ] @
Evo, već tri sata vežbam pokret diferenciranja arkustangensa. Još malo, pa sam ga uvežbao.
Rekao sam da su moja iskustva drugačija, a položio sam više matematičkih ispita od većine učesnika ove teme. Ne kažem da nisam uopšte radio zadatke, ali uvek prvo teoriju, pa onda zadatke, pri čemu vreme za vežbanje zadataka nije prelazilo 20% od vremena potrošenog na teoriju.
A što se tiče onih koji matematiku shvataju sportski, "daj da vidim kako idu zadaci yebeš teoriju", ja bih im dao zadatke poput 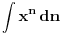 , pa bi padali ko zrele kruške.
Na tehničkim fakultetima se obično ne daju zadaci iz testa inteligencije, nego nešto od onoga što je rađeno na nastavi. Ako si razumeo teoriju vezanu za integraciju racionalnih funkcija, znaćeš i da rešiš zadatke. Isto važi i za integrale koji se standardnim smenama svode na integral racionalne funkcije. Za zadatke iz Furijeovih redova treba da znaš formule za koeficijente i teoreme o konvergenciji da bi to mogao da obrazložiš. Sve su to stvari koje pišu u teoriji.
[Ovu poruku je menjao Nedeljko dana 21.04.2009. u 13:35 GMT+1][ kingakul @ 21.04.2009. 15:00 ] @
Zasto bi padali kao kruske? Zato sto je po dn?
Kao prvo omalovazavanje matematike na "tehnickim fakultetima" je besmisleno jer se ne radi isto na svakom.
Drugo prava primena matematike kao i smisao svega se stice u strucnim predmetima. Slazem se da je potrebna teorija za Fourier-ove redove, ali isto tako mislim da nije dovoljna. Teorija je samo preduslov da se kasnije kroz strucne predmete razume sustina i primena. Moze neko da bude dobro matematicki potkovan iz teorije Fourier-ovih redova i da je presao Vise dimenzionalnu analizu tom 4, ali i dalje ne zna da primeni Fourier-ovu transformaciju u telekomunikacijama, obradi signala ili verovatnoci npr. Konkretno na ETF-u ima bar 4 predmeta gde se sve vrti oko FT, i reci da neko sa PMF-a to bolje razume zato sto je mozda vise prosao matematicku teoriju ne pije vodu.
[ Nedeljko @ 21.04.2009. 16:20 ] @
Ko omalovažava matematiku na tehničkim fakultetima?
Naravno da matematički fakultet gubi svaki smisao postojanja ako su kriterijumi na njemu u ravni sa kriterijumima na matematici na bilo kom drugom fakultetu i tu ne vidim nikakvo omalovažavanje ostalih fakulteta. Naprotiv, suprotan stav je omalovažavanje matematičkog fakulteta, a takvih priča sam se naslušao od raznih ETF-ovaca. Uporedi fond časova iz matematike i sve će ti biti jasno. To što je natrpano svašta u program i što se svaki od tih pojmova pomene, ne znači da je to zaista i obrađeno (kako treba). Kad pitaš solidne ETF-ovce čemu služi sistem rekurzivnih funkcija, reći će ti "za strogo definisanje sabiranja, množenja itd.". Ne daj bože da to ima ikakve veze sa algoritmima, npr. da bih znao da je neki problem algoritamski nerešiv, pa da ne bih ni pokušavao da ga isprogramiram. No, bitno je da su "radili" i Galoaovu teoriju. Ovo već jeste kritika (smatram osnovana) na račun bivšeg ETF-a. Stav da ni na jednom nematematičkom fakultetu matematika ne može da se radi ni približno kao na matematičkom ne govori ništa loše o tim drugim fakultetima.
Svojevremeno je na pismenom ispitu iz linearne algebre bio zadatak da opišeš skup svih kvadratnih realnih matrica koje imaju osobinu da su sve njihove komponente i sve komponente njihovih inverza nenegativni realni brojevi. Takvi zadaci ne bi priličili tehničkim fakultetima, ne zato što su studenti tehnike glupi, nego zato što imaju i druge predmete.
A što se tiče FT u filtriranju signala, ako si mislio na odsecanje donjeg dela FT i vraćanje rezultata inverznom transformacijom, tu i ne vidim neki overhead preko matematike. Do toga se lako kože doći i samo razumevanjem matiša, bez nekih dodatnih nematematičkih dosetki. No, pretpostavljam da ste osim toga učili i ozbiljnije fore, jer inače ne bi njegovi diplomci lako nalazili posao po belom svetu. To je ono zbog čega se školuju, a ne zbog trkanja sa matematičarima u matematici.
[ kingakul @ 21.04.2009. 16:50 ] @
Na matematickom fakultetu ima vise matematike i onda je logicno da se tamo radi dublje (ili teze kako studenti vole da kazu). Problem je sto znam studente koji su na PMF-u dali analizu 1 i 2 sa dobrim ocenama, a na ETF-u ne mogu da prodju Matematiku 2, za obrnute primere ne znam.
Ali, ti pojedinacni primeri nisu ni bitni. Sustina mog izlaganja je da se veci deo matematike na ETF-u ne uci u okviru Matematike[i.] (gde i ide od 1 do 5) ili kako se vec zovu (Numericka i diskretna, Verovatnoca i statistika...) vec se uci u okviru strucnih predmeta. Zato je obradjeno puno oblasti povrsno. Nisu svakom potrebna polja Galois-a, ali ko ode na telekomunikacije npr. on ce u okviru predmeta "teorija informacija i kodova" raditi Galois-a polja, njihovu primenu i implementirati algoritme (zastitne kodove) u nekom konkretnom programskom jeziku. Generalno sticem utisak da se matematika bolje nauci i razume kada je predaje inzenjer, a ne matematicar (za studente tehnike naravno), jer se ona duboko zalazi u primenu i smisao iste. Tako da u zavisnosti od smera i oblasti kojom se elektroinzenjer bavi potrebne su mu neke oblasti matematike (a ono sto mu je zaista potrebno vise se nauci u okviru strucnih predmeta nego "matematika").
[ Mikky @ 22.04.2009. 00:24 ] @
Citat: kingakul: Generalno sticem utisak da se matematika bolje nauci i razume kada je predaje inzenjer, a ne matematicar (za studente tehnike naravno), jer se ona duboko zalazi u primenu i smisao iste.
Ovo je tacno... ali samo za nas inzenjere i fizicare. Nama je matematika alat i kao takva, sama nam ne znacni ama bas nista. Mi u matematici ne vidimo smisao bez konkretne primene. Sa druge strane, matematicari su meni fascinantni ljudi. Oni je poimaju i bave se matematikom na jedan sasvim drugaciji nacin. Za njih je matematika kao umetnost (sto u sustini i jeste na neki nacin) i oni vide lepotu tamo gde je mi ne vidimo, inace je ne bi toliko voleli i studirali. Oni uce matematiku radi nje same i njima nije potreban dodatni smisao. Pa tako se cesto desava da imamo neke oblasti matematike koje su razvijene pre 150 godina a tek danas nalaze primenu. Taj dasa sto je razvijao to pre 150 godina nije to radio da bi pomogao covecanstvu u buducnosti ili nesto slicno vec je to radio iz nekog svog razloga znanog ili neznanog (verovatno ovog drugo) i bez nekog vidljivog smisla, a eto ispostavilo se da to moze kasnije da se primeni u realnom svetu na neki konkretan problem. On je u tome video neku lepotu, to mu je golicalo um i mastu i time se bavio. Motiv za njega je bila matematika radi same matematike.
Ja licno ne vidim smisao studiranja matematike kao takve same za sebe, to je kao jedna igra u koju je neko uveo neka pravila (aksiome) i sad mi treba da vidimo sta sve iz tih osnovnih pravila moze da se zakljuci na kraju. Ja se pitam onda zasto bi neko studirao neku igru sa bas takvim pravilima a ne nekim drugim? Ok mozda zato sto su ta osnovna pravila nastala na osnovu nekih karakteristika naseg univerzuma (aksiome euklidske geometrije) ali opet ta igra ni po cemu matematicki nije posebnija od nekih drugih. Tako su nastale i neke druge oblasti matematike, npr ona geometrija Lobachevskog koji je promenio jedno pravilo i dobio sasvim drugaciju igru koja nema bas veze sa nasim univerzumom ali nije ni po cemu manje matematika od standardne. Ali to sam samo ja a na srecu nisu svi kao ja vec imamo i matematicare jer su svetu ipak potrebni i ne moze se primenjivati matematika dok se dobro ne prouci bez gledanja u konkretan smisao. S druge strane nisu ni svi matematicari, i to je dobro jer bi onda imali samo gomilu apstraktnog znanja koje ne sluzi nicemu.
E sad kad se uporede ova dva razlicita pristupa svetu lako se dolazi do ovakvih diskusija gde matematicar i inzenjer ne mogu da dodju do nekog usaglasenog stava. Matematicaru nikad nece biti jasno kako mi ostali ne kapiramo to kao on i kako mozemo da polazemo ispite bez razumevanja i teorije, a inzenjeru nikad nece biti jasno sta ovaj tripuje toliko sa tom matematikom umesto da radi nesto konkretno. Svako tera svoju politiku. [ Farenhajt @ 22.04.2009. 01:00 ] @
Citat: MikkyPa tako se cesto desava da imamo neke oblasti matematike koje su razvijene pre 150 godina a tek danas nalaze primenu.
Pa upravo u tome i jeste poenta. Na neki način, matematičara možeš smatrati apstraktnom verzijom mašinskog inženjera: elektroinženjer ili građevinski inženjer dođe mašincu i kaže mu: "Meni treba mašina koja može da mi odradi takav i takav posao, relativno bezbedno i efikasno. Konstruiši mi je." Onda mašinac sedne za sto i konstruiše mašinu. Matematičar takođe konstruiše "mašine", ali ne za praktičnu nego intelektualnu upotrebu. S tim što se, kako i sam kažeš, često dešava da nadahnut matematičar stvori strukturu ("mašinu") za koju će se adekvatna inženjerska (praktična) primena naći tek mnogo kasnije. Ali to se dešava i mašincima: Leonardo je dao skice padobrana i helikoptera još u renesansi.
I u tome i jeste glavna suština raskoraka: inženjerska matematika uvek "kaska" za čistom, pošto prvo matematičar mora da konstruiše "mašinu", a inženjer kasnije da vidi da li mu ta "mašina" obavlja neki nužan posao. (Matematičar bi, recimo, bio dizajner koncept-automobila, sa koga se kasnije - a možda i nikad, nema veze - "skidaju" rešenja za serijske modele.)
I tako su jednog dana kompleksni brojevi, totalna apstrakcija, našli divnu i fenomenalnu primenu u proračunu prostoperiodičnih strujnih mreža, na kojima danas počiva čitav svet. No, matematičari se tu ne zaustavljaju. Prelaze na kvaternione i ostala čudesa, jer će možda jednog dana "zatrebati" - ali opet, možda i nikad neće, ali ne škodi da ih ima. [ GoranM @ 22.04.2009. 05:02 ] @
Citat: Nedeljko: Evo, već tri sata vežbam pokret diferenciranja arkustangensa. Još malo, pa sam ga uvežbao.
Mislim da nema potrebe za ovakvim banalizovanjem. Znas dobro na kakvo vezbanje sam mislio.
Ili su mozda pisci zbirki zadataka budale koje gube vreme, kao i oni koji ih resavaju?
Citat:
Rekao sam da su moja iskustva drugačija, a položio sam više matematičkih ispita od većine učesnika ove teme. Ne kažem da nisam uopšte radio zadatke, ali uvek prvo teoriju, pa onda zadatke, pri čemu vreme za vežbanje zadataka nije prelazilo 20% od vremena potrošenog na teoriju.
A što se tiče onih koji matematiku shvataju sportski, "daj da vidim kako idu zadaci yebeš teoriju", ja bih im dao zadatke poput 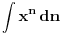 , pa bi padali ko zrele kruške.
Pa sad, nema razloga da ti ne verujem. Ipak, sustina je u tome da se na zadatke potrosi odredjeni broj sati koji je veci od nekog minimuma.
E sad, nekome je to 90% ukupno utrosenog vremena za matematiku, a nekome 10%.
Na ovoj temi se uglavnom okupljaju studenti dodiplomskih tehnickih studija kao i sredjoskolci. Davati njima savet da im treba samo teorija da bi dobili 8 je jednostavno pogresno. Naravno da odredjena kolicina teorije mora da se zna pre nego sto se bilo sta zapocne, a ne vidim da je iko tvrdio suprotno.
Ali ako neko studira matematiku, svakako ce potrositi vise vremena u apsolutnom smislu, na teoriju, od nekoga ko studira tehniku. A posebno u odnosu na sredjoskolca.
Citat:
Na tehničkim fakultetima se obično ne daju zadaci iz testa inteligencije, nego nešto od onoga što je rađeno na nastavi. Ako si razumeo teoriju vezanu za integraciju racionalnih funkcija, znaćeš i da rešiš zadatke. Isto važi i za integrale koji se standardnim smenama svode na integral racionalne funkcije. Za zadatke iz Furijeovih redova treba da znaš formule za koeficijente i teoreme o konvergenciji da bi to mogao da obrazložiš. Sve su to stvari koje pišu u teoriji.
[Ovu poruku je menjao Nedeljko dana 21.04.2009. u 13:35 GMT+1]
Velika je razlika izmedju znati kako uraditi nesto, i zaista uraditi to isto. Poznavanje teorije je potreban ali ne i dovoljan uslov.
Ako ni zbog cega drugog, onda uvezbanost treba zbog rutine i brzine resavanja zadataka na ispitu.
Sta god da covek hoce kvalitetno da radi, mora da bude uvezban. I to je nesto sto su ljudi otkrili pre jako mnogo vremena :-)
[Ovu poruku je menjao GoranM dana 22.04.2009. u 07:59 GMT+1][ GoranM @ 22.04.2009. 06:42 ] @
Citat: kingakul: Zasto bi padali kao kruske? Zato sto je po dn?
Kao prvo omalovazavanje matematike na "tehnickim fakultetima" je besmisleno jer se ne radi isto na svakom.
Drugo prava primena matematike kao i smisao svega se stice u strucnim predmetima. Slazem se da je potrebna teorija za Fourier-ove redove, ali isto tako mislim da nije dovoljna. Teorija je samo preduslov da se kasnije kroz strucne predmete razume sustina i primena. Moze neko da bude dobro matematicki potkovan iz teorije Fourier-ovih redova i da je presao Vise dimenzionalnu analizu tom 4, ali i dalje ne zna da primeni Fourier-ovu transformaciju u telekomunikacijama, obradi signala ili verovatnoci npr. Konkretno na ETF-u ima bar 4 predmeta gde se sve vrti oko FT, i reci da neko sa PMF-a to bolje razume zato sto je mozda vise prosao matematicku teoriju ne pije vodu.
Inzenjerima je matematika alat koji moraju solidno da poznaju da bi mogli da ga koriste. Ili bolje receno, komplet alata.
Citavi doktorati iz tehnickih nauka su napisani, a koji se bave analizom resenja neke parcijalne diferencijalne jednacine
primenjene na neki praktican problem. Ili jos bolje sistema istih.
Samo ta parcijalna diferencijalna jednacina, moze biti trivijalna za nekog matematicara. Ali za inzenjera koji analizira, na primer, vibracije
nekog mosta, ili raspodelu elektromagnetnog polja unutar nekog prostora, ili nesto trece, ta jednacina i njena resenja imaju sasvim drugaciji
smisao od same matematicke strane problema.
[Ovu poruku je menjao GoranM dana 22.04.2009. u 08:02 GMT+1][ Nedeljko @ 22.04.2009. 08:58 ] @
Citat: kingakul: Na matematickom fakultetu ima vise matematike i onda je logicno da se tamo radi dublje (ili teze kako studenti vole da kazu). Problem je sto znam studente koji su na PMF-u dali analizu 1 i 2 sa dobrim ocenama, a na ETF-u ne mogu da prodju Matematiku 2, za obrnute primere ne znam.
Ja ne znam ni za primere onih sa ETF-a koji su pokušavali da polože analizu 1 i 2 na MATF-u, pa samim tim ne znam ni za one koji su ih položili.
Citat: kingakul: Nisu svakom potrebna polja Galois-a, ali ko ode na telekomunikacije npr. on ce u okviru predmeta "teorija informacija i kodova" raditi Galois-a polja, njihovu primenu i implementirati algoritme (zastitne kodove) u nekom konkretnom programskom jeziku.
Teorija Galoa i Galoaova polja nemaju skoro nikakve međusobne veze. Galoaova polja su ništa drugo do konačna polja, dok se teorija Galoa radi sa normalnim, separabilnim raširenjima konačnog stepena (koja se zovu Galoaova raširenja). Termini su slični, ali su sadržaji potpuno različiti.
Citat: kingakul: Generalno sticem utisak da se matematika bolje nauci i razume kada je predaje inzenjer, a ne matematicar (za studente tehnike naravno), jer se ona duboko zalazi u primenu i smisao iste. Tako da u zavisnosti od smera i oblasti kojom se elektroinzenjer bavi potrebne su mu neke oblasti matematike (a ono sto mu je zaista potrebno vise se nauci u okviru strucnih predmeta nego "matematika").
Upravo sam pokazao da se na ETF-u nije mogao videti nikakav smisao onoga što se uči.
Citat: Nedeljko: Kad pitaš solidne ETF-ovce čemu služi sistem rekurzivnih funkcija, reći će ti "za strogo definisanje sabiranja, množenja itd.". Ne daj bože da to ima ikakve veze sa algoritmima, npr. da bih znao da je neki problem algoritamski nerešiv, pa da ne bih ni pokušavao da ga isprogramiram. No, bitno je da su "radili" i Galoaovu teoriju.
To što se učilo nije se učilo da bi se naučilo i primenjivalo, već da bi u nastavnom planu i programu pisalo da se to uči, te da bi ETF imao neku polumatičnost za oblast matematike (tj. da bi asistente regrutovao iz svojih redova).
Imaš po Engleskoj građevinskih fakulteta bez ijednog matematičkog/fizičkog predmeta, ali sa diplomom takvog fakulteta ćeš da se ubiješ tražeći posao. Na onim fakultetima po svetu koji su bolji od naših i koji nam mogu biti uzor tih predmeta ima i više nego kod nas, predaje ih onaj ko treba da ih predaje, a programe određuju inženjeri. [ Nedeljko @ 22.04.2009. 09:03 ] @
Citat: GoranM: Mislim da nema potrebe za ovakvim banalizovanjem. Znas dobro na kakvo vezbanje sam mislio.
Samo sam pokazao koliko to ima veze sa sportom i borilačkim veštinama.
Citat: GoranM: Pa sad, nema razloga da ti ne verujem. Ipak, sustina je u tome da se na zadatke potrosi odredjeni broj sati koji je veci od nekog minimuma.
To jet tvoj je problem da li ćeš mi veoravati.
Citat: GoranM: Velika je razlika izmedju znati kako uraditi nesto, i zaista uraditi to isto. Poznavanje teorije je potreban ali ne i dovoljan uslov.
Ako ni zbog cega drugog, onda uvezbanost treba zbog rutine i brzine resavanja zadataka na ispitu.
Sta god da covek hoce kvalitetno da radi, mora da bude uvezban. I to je nesto sto su ljudi otkrili pre jako mnogo vremena :-)
Ako zaista znaš kako nešto da uradiš, onda treba još samo da zavrneš rukave da bi to uradio. Da, sticanjem rutine se neke stvari rade brže i to je sve. Druga je stvar što je stepen razumevanja teorije kod studenata da pitaju "A šta će mi to?". [ miki069 @ 22.04.2009. 13:31 ] @
Ako neko položi sa ocenom 6 Analizu 1 i 2 i samo odsluša Algebru polaže matematike 1,2 i 3 na svim tehničkim fakultetima sa ocenama 10.
Obrnuto ne važi. Nema šanse.
Jeste li ikada videli zadatke sa pismenog iz Analize ili Algebre sa PMF-a u Beogradu, Kragujevcu, Nišu...?
Da jeste ne biste pisali nebuloze.
Ja kad ih vidim zamislim se... podobro...
Ako hoćete postovaću neki.
Za zadatke sa tehničkih fakulteta mi treba vremena koliko mi treba za pisanje. Nijedan ne traži razmišljanje. A nisam u nekoj formi za zadatke.
Pa svaki gimnazijalac može odmah da položi matematiku 1, a posle odslušanih diferencijalnih jednačina i matematiku 2 na svim tehničkim fakultetima.
Matematika 3 se ne obradjuje u gimnazijama.
matematike 4 i 5 nemaju svi tehnički fakulteti već samo neki.
[ Nedeljko @ 22.04.2009. 13:54 ] @
Citat: miki069: Pa svaki gimnazijalac može odmah da položi matematiku 1, a posle odslušanih diferencijalnih jednačina i matematiku 2 na svim tehničkim fakultetima.
Malo si preterao, ali priznajem da sam i ja preterao.
Daleko od toga da matematika na ETF-u ništa nije valjala. U tom slučaju ne bi taj fakultet proizvodio elektroinženjere koji se sa tom diplomom lako zapošljavaju po belom svetu. No, oni se ne zapošljavaju po belom svetu kao matematičari, jer ta diploma nije cenjena za to, već kao elektroinženjeri, softveraši itd.
ETF jeste bio kvalitetniji fakultet za svoju oblast, nego MATF za svoju, mada ni diplome MATF-a nisu za bacanje. Moj drug sa generacije se posle završenih studija matematike u BG i položenog GRE ladno zaposlio kao asistent na MIT-u (a to je najugledniji univerzitet za tehničke nauke u svetu). Znam za slučaj žene kojoj je diploma teorijskog smera MATF-a priznata u Švedskoj na doktorskim studijama kao pun fakultet + 3 od 6 doktorskih ispita, a nije doktorirala na "š" univerzitetu, jer je posle toga radila kao profesorka na Kolumbija univerzitetu, SAD.
No, kompleksi ETF-a da moraju da regrutuju asistente iz matematike i fizike iz svojih redova su samo naneli štetu nastavi tih predmeta na njemu.
Citat: Nedeljko: To što se učilo nije se učilo da bi se naučilo i primenjivalo, već da bi u nastavnom planu i programu pisalo da se to uči, te da bi ETF imao neku polumatičnost za oblast matematike (tj. da bi asistente regrutovao iz svojih redova).
Ovo je tačno za jedan deo gradiva. Naravno, mnoge oblasti su primenjivali i videli svrhu njihovog postojanja. [ pri3rak @ 22.04.2009. 14:08 ] @
Citat: Nedeljko:
No, kompleksi ETF-a da moraju da regrutuju asistente iz matematike i fizike iz svojih redova su samo naneli štetu nastavi tih predmeta na njemu.
Au pa tu bas grdno gresis ;) [ GoranM @ 23.04.2009. 05:14 ] @
Citat: pri3rak: Au pa tu bas grdno gresis ;)
Ma zar nisi cuo da zli ETF-ovci planiraju i profesore stranih jezika da regrutuju iz svojih redova :))))
A sad ozbiljno, nazivati nastavnicki kadar jedne od najboljih obrazovnih institucija u Srbiji kompleksasima,
jednostavno ne zasluzuje komentar. Da napomenem da nastavnike i saradnike nekog fakulteta bira
nastavno-naucno vece tog fakulteta. Iako se ETF moze i treba kritikovati zbog mnogo toga,
ovaj tip kritike samo govori o kriticaru a ne o onima kojima je kritika upucena. [ GoranM @ 23.04.2009. 05:43 ] @
Citat: Nedeljko: Samo sam pokazao koliko to ima veze sa sportom i borilačkim veštinama.
Ne. Ali si pokazao da se lepo sluzis doskocicama. To samo po sebi nije lose, ali ni na koji nacin ne doprinosi diskusiji.
No, ako ti se primer nije svideo, evo imam drugi:
Uzme covek i nauci note. I ne samo to, nauci i gde je koja na klaviru (moze i na harmonici). I onda kaze,
evo ja znam da sviram klavir/harmoniku. Mogu da odsviram sta 'oces.
E ja kazem, ne ne znas. Idi malo provezbaj pa ces mozda znati za koju godinu.
Citat: Nedeljko: To jet tvoj je problem da li ćeš mi veoravati.
Bravo majstore! Kakva argumentacija i konstruktivan doprinos diskusiji.
Vidi, hteo sam jos nesto da napisem, no posto videh gore da veselo diskutujes sam sa sobom,
rekoh sto ja sad da nekome kvarim srecu.
[Ovu poruku je menjao GoranM dana 24.04.2009. u 08:22 GMT+1][ GoranM @ 23.04.2009. 07:22 ] @
Nego da se vratimo na temu. Za prepucavanja tipa MATF vs ETF i slicno predlazem otvaranje nove teme pa ko voli nek izvoli.
Mada verujem da vec ima pootvaranih tema tog tipa.
Dakle, tema ovde je kako uciti matematiku.
Evo mozemo da uzmemo za primer matematiku 2 sa ETF-a, kad se vec ETF toliko pominje.
Da bi se polozila matematika 2, na ETF-u, potrebno je uzeti knjigu od Milana Merklea "Matematicka Analiza: Pregled Teorije i Zadaci".
Svojevremeno je stampana na nekom debljem pa papiru pa je to bila bas debela knjizurina. Prosecnog studenta muka da uhvati cim
je pogleda. Uz ovu knjigu ide i "Matematicka Analiza: Teorija", koja je isto neophodna za polaganje drugog dela ispita, mada se
vecina stvari iz te knjige nalazi i u ovoj prvoj. Ovde napominjem da se ova literatura koristila svojevremeno, mnogo pre Bolonje.
Verujem da je i sada isto ili jako slicno.
E dalje se sedne negde i krene redom, prouci se teorija na pocetku svakog poglavlja i krene da se radi jedan po jedan zadatak.
Ovde je jako vazno da se resavanje svakog zadatka dovede do kraja, i da se nikako ne upada u zamku "e dalje znam".
Znaci disciplinovano i do kraja. Vremenom, covek primeti da mu zadaci idu sve bolje, kao i da sve bolje razume teoriju.
Mnoge stvari koje su potrebne na teorijskom delu ispita, na primer za dokazivanje teorema, su date kroz zadatke tako da
covek usvaja ove tehnike vezbajuci. Kad se dodje do kraja knjige, onda treba krenuti od pocetka i proraditi "sve" jos jednom.
Drugi prolaz ce ici mnogo brze, i sam osecaj da se napreduje dodatno motivise studenta i uliva samopouzdanje.
Na kraju, ko ovo prodje 2 puta, garantovano ce poloziti ispit i to sa visokom ocenom.
Potpuno isti pristup treba primeniti za sve druge matematike, fizike, OET-e, TEK-ove, itd.
Ovo jeste tesko. Zahteva jako mnogo vremena. Pogotovo na pocetku. Na nizim godinama. Kasnije sve ide mnogo brze.
Ja licno nisam uvek ovako radio. No tamo gde jesam, uvek sam jako dobro prolazio na ispitima i te materije se secam i danas.
E da, ne nasedajte na price ljudi koji kazu, ma to se sprema 2 dana i slicno. Mislim da je svako ko je bio na ETF-u cuo pricu tipa:
"ja poceo da spremam ispit pre 2 dana. Juce sam isao na basket, a posle otisao na zurku, napio se a imao ispit jutros u osam."
I onda kad pitas "A kako si uradio?" dobijes odgovor "Ma uradio sam sve...". ;-)
Neki ljudi imaju potrebu da se predstave drugima kao jako pametni, a sve u cilju dobijanja nekog priznanja.
Jos jedna stvar. Najveca vrednost zavrsenog fakulteta je ta da vas tamo nauce da ucite, i da izgradite radne navike.
Na samom fakultetu cete uciti gomilu stvari koje vam kasnije nece trebati. Isto tako, dosta toga sto ce vam trebati, necete
nauciti na fakultetu, nego cete morati kasnije sami. Zato ko god je prosao kroz ovaj dril, imace bolje predispozicije za to.
Sad sve ovo sto sam vam rekao je pronalazenje rupe na saksiji. No smatram da je vazno da se prenese sto vise
raznih iskustava. Eto toliko od mene. Pozdrav svima!
[ Nedeljko @ 23.04.2009. 11:13 ] @
Citat: pri3rak: Au pa tu bas grdno gresis ;)
Za razliku od tebe, ja sam svoj stav obrazložio.
Citat: GoranM: Ma zar nisi cuo da zli ETF-ovci planiraju i profesore stranih jezika da regrutuju iz svojih redova :))))
A sad ozbiljno, nazivati nastavnicki kadar jedne od najboljih obrazovnih institucija u Srbiji kompleksasima,
jednostavno ne zasluzuje komentar. Da napomenem da nastavnike i saradnike nekog fakulteta bira
nastavno-naucno vece tog fakulteta. Iako se ETF moze i treba kritikovati zbog mnogo toga,
ovaj tip kritike samo govori o kriticaru a ne o onima kojima je kritika upucena.
Boli mene uvo odakle će oni nkoga da regrutuju, meni to ne ide ni iz džepa ni u džep. ETF-ovci mi ni najmanje nisu konkurencija. No, smatram da su pre svega studenti ETF-a zbog toga pretpeli štete. Ne kažem ja da oni nisu ništa iz matematike naučili kako treba, jer je ETF spadao u vrlo kvalitetne fakultete u svetu, s tim da njegovi diplomci nisu lako nalazili posao van ex YU prostora kao matematičari, već kao inženjeri. To što je neko završio ETF apsolutno ne znači da će biti uspešan režiser.
Unošenje nekog sadržaja u program samo da bi u programu pisalo da se to radi ne smatram prirodnim i normalnim. A što se kompleksa tiče, najelitniji krugovi su najrizičnije grupe za dobijanje kompleksa. Prošetajte do MATF-a i raspitajte se na šta liče naučno nastavna veća - čak im je i milicija više puta intervenisala. Pročitajte čuvenu prepisku između Alberta Ajnštajna i Nilsa Bora, koja nije imala blage veze sa naukom, već samo sa vređanjem na ličnoj osnovi sa ciljem utvrđivanja "čiji je veći". U ratu diferencijalnog računa je Ser Isak Njutn formirao komisiju za utvrđivanje ko je otkrio diferencijalni i integralni račun (Ser Isak Njutn ili Gotfrid Vilhelm Lajbnic). Komisiju koja je Lajbnica nazvala svakakvim imenima su činila dva lekara, fizičar Huk, Astronom Halej i predsednik komisije Ser Isak Njutn. To što je neko pametan ne znači da nije kompleksaš i to nisu izuzeci, već je upravo ta grupa visoko rizična.
Citat: GoranM: Ne. Ali si pokazao da se lepo sluzis doskocicama. To samo po sebi nije lose, ali ni na koji nacin ne doprinosi diskusiji.
No, ako ti se primer nije svideo, evo imam drugi:
Uzme covek i nauci note. I ne samo to, nauci i gde je koja na klaviru (moze i na harmonici). I onda kaze,
evo ja znam da sviram klavir/harmoniku. Mogu da odsviram sta 'oces.
E ja kazem, ne ne znas. Idi malo provezbaj pa ces mozda znati za koju godinu.
Posto kazes da si uvezbao potez diferenciranja arkustangensa ili sta je vec bilo, i pitao si me sta dalje,
evo ja predlazem da sad uvezbas sviranje integraljenja kosinusa. Lako je i nece ti trebati puno vremena.
Posle toga mozes da nastavis redom, po tablici, pa da nam na kraju odrzis koncert. Da ne padamo ko zrele kruske :-D
Matematika ima veze sa muzikom, koliko i sa sportom. Npr. muzika je ril tajm proces. Ne možeš da sviraš brže dok si odmoran, pa na kraju sporije kada se umoriš. Ne zahteva racionalno rasuđivanje, već sasvim druge moždane aktivnosti. To nikako nije uporedivo. Ako ne veruješ meni, probaj svoju tezu da objasniš muzičarima.
Citat: GoranM: Bravo majstore! Kakva argumentacija i konstruktivan doprinos diskusiji.
Vidi, hteo sam jos nesto da napisem, no posto videh gore da veselo diskutujes sam sa sobom,
rekoh sto ja sad da nekome kvarim srecu.
Ovo je argumentacija koja je dala vrhunski doprinos diskusiji
Citat: GoranM: Pa sad, nema razloga da ti ne verujem.
Da li si razmišljao malo o ovakvoj "argumentaciji" upućenoj u suprotnom smeru? Zašto bi iko verovao tebi bilo šta što napišeš? [ pri3rak @ 23.04.2009. 11:38 ] @
Citat: Nedeljko:
Za razliku od tebe, ja sam svoj stav obrazložio.
jesi priznajem :)
1. nije istina da komplexasi ili ko vec regrutuju asistente samo iz svojih redova, ako bas insistiras mogu i imena onih koji su meni drzali vezbe da navodim, a poreklo im je svima do jednog sa matematickih fakulteta (pazi to je bilo 5 predmeta) ....
2. inzenjeri nisu matematicari niti ima potrebe da uce matematiku na isti nacin, a pogotovu ne u istim kolicinama, a treba imati u vidu da uopste nije lose da barem neki ljudi na katedri imaju inzenjersko poreklo zbog mnogo boljeg uvida u aparat koji se koristi u struci kao i metodologiju struke koju matematicari jednostavno nemaju
3. od cistih matematicara, inzenjeri koji postaju matematicari umeju da smore jos gore svojim formalizmom (ona prica o postojanju veceg katolika od pape), goran je vec pomenuo merkleovu knjigu iz analize, e gori smor od knjige se na etf-u stvarno tesko nadje (cast cajnoj elektronici ona nema premca), vec sledece godine covek nadje lep inzenjerski udzbenik iz matematike III od tosica i vidi da to ne mora da bude toliko nenormalno dosadno i naporno,a da pri tome bude korisno i sasvim dovoljno za predmete koji se naslanjaju na taj aparat ....
4. nekad katedre iz struke umeju da budu toliko razocarane ponetim znanjem iz matematike pa inicjativno drze svoje manje kruseve za potrebe predmeta, primer su telekomunikacije gde profesor nakon sto dobro ispljuje poneto znanje iz verovatnoce uradi tacno ono sto njemu treba za predmet .... [ miki069 @ 23.04.2009. 13:33 ] @
Matematika 1 i 2 na tehničkim fakultetima danas i pre 10-15-20 godina se razlikuju mnogo.
Kvalitet je opao mnogo.
Ovo danas je nivo gimnazije.
Već smo komentarisali zadatke sa pomenutih linkova.
Smešno.
80% zadataka je iz Venove zbirke za 3 i 4 godinu srednje škole.
Naši fakulteti su nekada sa razlogom bili cenjeni u odnosu na zapadne.
Sad su po Bolonji isti i ne verujem da će generacije koje sad studiraju imati ulaz na MiT i Kolumbiju kao pre 15 godina.
[ Nedeljko @ 23.04.2009. 14:06 ] @
Citat: pri3rak: 1. nije istina da komplexasi ili ko vec regrutuju asistente samo iz svojih redova, ako bas insistiras mogu i imena onih koji su meni drzali vezbe da navodim, a poreklo im je svima do jednog sa matematickih fakulteta (pazi to je bilo 5 predmeta) ....
2. inzenjeri nisu matematicari niti ima potrebe da uce matematiku na isti nacin, a pogotovu ne u istim kolicinama, a treba imati u vidu da uopste nije lose da barem neki ljudi na katedri imaju inzenjersko poreklo zbog mnogo boljeg uvida u aparat koji se koristi u struci kao i metodologiju struke koju matematicari jednostavno nemaju
3. od cistih matematicara, inzenjeri koji postaju matematicari umeju da smore jos gore svojim formalizmom (ona prica o postojanju veceg katolika od pape), goran je vec pomenuo merkleovu knjigu iz analize, e gori smor od knjige se na etf-u stvarno tesko nadje (cast cajnoj elektronici ona nema premca), vec sledece godine covek nadje lep inzenjerski udzbenik iz matematike III od tosica i vidi da to ne mora da bude toliko nenormalno dosadno i naporno,a da pri tome bude korisno i sasvim dovoljno za predmete koji se naslanjaju na taj aparat ....
4. nekad katedre iz struke umeju da budu toliko razocarane ponetim znanjem iz matematike pa inicjativno drze svoje manje kruseve za potrebe predmeta, primer su telekomunikacije gde profesor nakon sto dobro ispljuje poneto znanje iz verovatnoce uradi tacno ono sto njemu treba za predmet ....
1. Da bi imao makar jednog asistenta iz svojih redova, moraš imati neku (polu)matičnost, a da bi imao matičnost, moraš da praviš gluposti na nastavi kakve sam naveo i koje veliku većinu studenata dave. Drugo su SAD koje nemaju zakon o univerzitetu, gde se univerziteti uzajamno kontrolišu konkurisanjem i gde možeš klošara da postaviš za profesora ako smatraš da ti je to u interesu. Rejmond Smajlian je držao predavanja iz kalkukusa (naša analiza 1 i 2), a da ga nikada niej položio.
2. Ipak mislim da ni ovde nisi u pravu jer
a) Osobine integrala ne zavise od područja njegove primene. Može se kurs optimizovati ka nekim primenama, ali je za to dovoljno reći matematičarima koje tipove da rade itd.
b) Bolji tehnički univerziteti od naših imaju više matematike i predaju je matematičari.
Citat: miki069: Matematika 1 i 2 na tehničkim fakultetima danas i pre 10-15-20 godina se razlikuju mnogo.
Kvalitet je opao mnogo.
Ovo danas je nivo gimnazije.
Već smo komentarisali zadatke sa pomenutih linkova.
Smešno.
80% zadataka je iz Venove zbirke za 3 i 4 godinu srednje škole.
Naši fakulteti su nekada sa razlogom bili cenjeni u odnosu na zapadne.
Sad su po Bolonji isti i ne verujem da će generacije koje sad studiraju imati ulaz na MiT i Kolumbiju kao pre 15 godina.
Nemoj samo da misliš da kvalitet studija matematike kod nas nije opao. Opalo je sve. Mada, ona žena koja je upisala doktorske studije u Švedskoj sa priznavanjem diplome kao fakulteta + 3 od 6 doktorskih ispita je doktorske studije upisala negde 2004. [ pri3rak @ 23.04.2009. 14:30 ] @
Citat: Nedeljko:
1. Da bi imao makar jednog asistenta iz svojih redova, moraš imati neku (polu)matičnost, a da bi imao matičnost, moraš da praviš gluposti na nastavi kakve sam naveo i koje veliku većinu studenata dave. Drugo su SAD koje nemaju zakon o univerzitetu, gde se univerziteti uzajamno kontrolišu konkurisanjem i gde možeš klošara da postaviš za profesora ako smatraš da ti je to u interesu. Rejmond Smajlian je držao predavanja iz kalkukusa (naša analiza 1 i 2), a da ga nikada niej položio.
bojim se da ovde ne kapiram sta si hteo da kazes imajuci u vidu da sam ja samo rekao da nije istina da se asistentni na katedri za metematiku biraju samo iz redova inzenjera koji su zavrsili etf i rekao sam da se to vrlo lako moze potkrepiti imenima i prezimenima ...
Citat: Nedeljko:
2. Ipak mislim da ni ovde nisi u pravu jer
a) Osobine integrala ne zavise od područja njegove primene. Može se kurs optimizovati ka nekim primenama, ali je za to dovoljno reći matematičarima koje tipove da rade itd.
b) Bolji tehnički univerziteti od naših imaju više matematike i predaju je matematičari.
a) da naravno, ali pitanje je kakve ces probleme iz integralnog racuna predstaviti studentima imajuci u vidu primene, a za ono sa cime ce se studenti tokom ostatka skolovanja sretati sigurno nije potreban neki posebno vrstan matematicar, pa cak ni neko ko je zavrsio striktno samo osnovne studije matematike
inace na etf-u je pre postojalo usmerenje na postdiplomskim studijama koje se bavilo samo matematikom primenjenom u elektrotehnici i verujem da je to bilo sasvim dovoljno za potrebe fakulteta, ali eto i poed njih primano je dosta ljudi s strane sto svakako nije lose
b) ne znam kako je sada, ali ranije nije bilo tako, cak je bilo obrnuto ...
[Ovu poruku je menjao pri3rak dana 23.04.2009. u 15:43 GMT+1][ kingakul @ 23.04.2009. 17:36 ] @
Citat: miki069Ako neko položi sa ocenom 6 Analizu 1 i 2 i samo odsluša Algebru polaže matematike 1,2 i 3 na svim tehničkim fakultetima sa ocenama 10.
Obrnuto ne važi. Nema šanse.
Ja znam za konkretne primere tako da vazi (dokaz kontradikcijom). Sada mozda Analiza 1/2 variraju od smera do smera, ali konkretno na smeru informatika znam ljude koji su dobili 7,8 a matu 2 na ETF padaju vec 5,6 put. Ne znam da li se to razlikuje od smera do smera.
edit: nasao sam i razlikuje se i to znacajno (na informatici je Analiza 1 jednosemestralni predmet 3+2, a na ostalim Analiza 1 dvosemestralni 4+4, znaci ogromna razlika):
http://www.matf.bg.ac.yu/planovi/novi1.html
http://www.matf.bg.ac.yu/planovi/novi2.html
Citat: miki069Pa svaki gimnazijalac može odmah da položi matematiku 1, a posle odslušanih diferencijalnih jednačina i matematiku 2 na svim tehničkim fakultetima.
Ovo uopste nije tacno bar ne za ETF, pored diferencijalnih jednacina ne rade se ni redovi, teorija grafova, opsta algebra, bulova algebra, i gomila nekih pojedinacnih stvari poput nekih metoda integraljenja, nekih stvari iz linearne algebre + na sve to teorija koja se uopste ne radi u gimnazijama (dakle gomila dokaza, teorema...)
Citat: GoranM Uzme covek i nauci note. I ne samo to, nauci i gde je koja na klaviru (moze i na harmonici). I onda kaze,
evo ja znam da sviram klavir/harmoniku. Mogu da odsviram sta 'oces.
Naravno mora da zna sta je spektar, malo da prouci modulacije pa tek onda... :)
Salu na stranu primer je dobar.
Citat: Nedeljkoa) Osobine integrala ne zavise od područja njegove primene. Može se kurs optimizovati ka nekim primenama, ali je za to dovoljno reći matematičarima koje tipove da rade itd.
Naravno da nama zavise - ne ispoljavaju se sve osobine u svakoj primeni. Ne zanima me kompleksna analiza da bih resio integral f(t)*e^jwt dt.
Citat: NedeljkoNo, kompleksi ETF-a da moraju da regrutuju asistente iz matematike i fizike iz svojih redova su samo naneli štetu nastavi tih predmeta na njemu.
Meni je jako tesko da vodim ovu diskusiju, kad pogledam na sat na kompu pise 2009. godina, a iz price imam utisak da su 80te. Jel mi pricamo o ETF-u, PMF-u i kako uciti matematiku sada ili pre 30 (slovima: trideset) godina.
Na danasnjem ETF-u, ako se ne varam, postoji samo 1 clan katedre za matematiku koji nije matematicar vec elektroinzenjer. Svi ostali su matematicari. A matematika je po mom misljenju jako lose odradjena na ETF-u (ne kazem da je laka niti da ju je lako poloziti nego kazem da je faktor dobrote los, korisno_nauceno/ulozeno_vreme je malo).
Fiziku predaju elektroinzenjeri, ali oni su potpuno maticni za tu oblast (ovi sa katedre za tehnicku fiziku odnosno smera za fizicku elektroniku), isto kao sto su racunarci (RTI tj. IR, SI) maticni za svoje predmete.
Koliko ja znam na FON-u su svi asistenti/profesori matematike FON-ovci, e ako su oni maticni onda super... na njih se niko ne buni ovde izgleda.
Citat: pri3rak3. od cistih matematicara, inzenjeri koji postaju matematicari umeju da smore jos gore svojim formalizmom (ona prica o postojanju veceg katolika od pape), goran je vec pomenuo merkleovu knjigu iz analize, e gori smor od knjige se na etf-u stvarno tesko nadje (cast cajnoj elektronici ona nema premca), vec sledece godine covek nadje lep inzenjerski udzbenik iz matematike III od tosica i vidi da to ne mora da bude toliko nenormalno dosadno i naporno,a da pri tome bude korisno i sasvim dovoljno za predmete koji se naslanjaju na taj aparat .... Meni je Merkleova analiza super knjiga i zanimljiva. Ali onda opet ja imam afinitet prema analizi, ona knjiga iz algebre i teorija iz nje je dosadna do bola. Sta se Caje tice zvucis kao neki RTI-ovac sa produzenim studentskim stazom.
Citat: Nedeljkob) Bolji tehnički univerziteti od naših imaju više matematike i predaju je matematičari.
Navedi primer (da imaju vise). Konkretno navedi neki EECS npr.
Evo na stanfordu (koji je verovatno prvi na svetu za CS) Knuth je dugo godina drzao concrete mathematics. Sta se mene tice ok nek se uvede i na ETF-u predmet "konkretna matematika".
[Ovu poruku je menjao kingakul dana 24.04.2009. u 00:42 GMT+1]
[Ovu poruku je menjao kingakul dana 24.04.2009. u 00:42 GMT+1][ pri3rak @ 23.04.2009. 17:51 ] @
Citat: kingakul:
Sta se Caje tice zvucis kao neki RTI-ovac sa produzenim studentskim stazom.
uzmi belu cajinu knjigu, pa pokusaj iz nje da ucis teoriju poluprovodnika (veci broj gresaka od onih u znaku do bas velikih na jednom mestu tesko je naci)
inace sa afinititetom za analizu kukas na onakve rokove? [ kingakul @ 23.04.2009. 18:37 ] @
sta to znaci kukam na rok? ne kukam ja nista nego kazem da na ETF-u znati logaritamski izvod vredi 4 poena od 100 (nakon sto si polozio eliminacioni) a npr. na fonu: http://mata.fon.rs/uploaded/mat1/pismeni/mm1_2008_feb.pdf
ima 4 zadataka jedan je limes koji se resava u 2-3 reda drugi funkcija koja se stvarno tesko ispituje.
samo sam hteo da opovrgnem to besmisleno napadanje kako je na ETF-u najlaksa matematika i kako je tu najveca kriza i degradacija. a na fonu (na kome fon-ovci predaju matematiku) ocigledno moze gimnazijalac da polozi ispit bez spremanja ako je imao 4 ili 5 u prosecnoj gimnaziji. dakle manite se vise ETF-a ima vecih problema... [ GoranM @ 24.04.2009. 06:15 ] @
Citat: Nedeljko: Da li si razmišljao malo o ovakvoj "argumentaciji" upućenoj u suprotnom smeru? Zašto bi iko verovao tebi bilo šta što napišeš?
Nedeljko, ocigledno nisi pazljivo procitao tu recenicu. Procitaj opet sta sam tamo napisao.
[ GoranM @ 24.04.2009. 06:53 ] @
Posto je tema ucenje matematike, a pominjan je MIT, evo ljudi su se potrudili i okacili sve :
http://ocw.mit.edu/OcwWeb/web/.../courses/index.htm#Mathematics
Mislim da je i Stanford odradio slicnu stvar.
[ pri3rak @ 24.04.2009. 10:26 ] @
MIT ima i cisto matematicko usmerenje ...
[ Nedeljko @ 24.04.2009. 12:21 ] @
Citat: kingakul: Ja znam za konkretne primere tako da vazi (dokaz kontradikcijom). Sada mozda Analiza 1/2 variraju od smera do smera, ali konkretno na smeru informatika znam ljude koji su dobili 7,8 a matu 2 na ETF padaju vec 5,6 put. Ne znam da li se to razlikuje od smera do smera.
A, tako. E, pa vidiš, oni nemaju zajedničku matematiku sa smerovima M (teorijski), R (računarski), V (verovatnoća i statistika) i N (numerička matematika i optimizacija), već drastično redukovane i programe i kriterijume na matematičkim predmetima. Čak im je i broj matematičkih predmeta nešto manje. Sa završenim I smerom (informatika) se stiče zvanje "diplomirani informatičar" (dakle, ne matematičar), a sa ona četiri "diplomirani matematičar za ...". Tu postoji velika razlika. [ Nedeljko @ 24.04.2009. 13:04 ] @
Citat: pri3rak: uzmi belu cajinu knjigu, pa pokusaj iz nje da ucis teoriju poluprovodnika (veci broj gresaka od onih u znaku do bas velikih na jednom mestu tesko je naci)
Preporučujem knjige "Diferencijalne jednačine" autora J. Knežević-Miljanović, R. Protić, M. Šćepanović i "Diferencijalna geometrija" autora N. Bokan i M. Blažić. Imao sam nesreću da učim iz njih.
Dakle, knjige kakve tražiš je vrlo lako naći. [ pri3rak @ 24.04.2009. 13:07 ] @
ma ja sam mislio samo na ETF literaturu,a ne nesto u sirem smislu :)
[ Nedeljko @ 24.04.2009. 13:18 ] @
Ako te zanimaju knjige sa ogromnim brojem grešaka na jednom mestu, preporučio sam ti literaturu sa MATF-a. U "Diferencijalnoj geometriji" imaš čak i slučaj sa bar tri greške u jednoj rečenici.
[ Nedeljko @ 24.04.2009. 13:41 ] @
Citat: GoranM: Nedeljko, ocigledno nisi pazljivo procitao tu recenicu. Procitaj opet sta sam tamo napisao.
Pa, napisao si
Citat: GoranM: Pa sad, nema razloga da ti ne verujem.
Ja ti prenesem svoja iskustva, a ti napišeš ovako nešto. Primeni tu istu "argumentaciju" u suprotnom smeru. [ Cabo @ 24.04.2009. 15:50 ] @
Citat: Nedeljko: Preporučujem knjige "Diferencijalne jednačine" autora J. Knežević-Miljanović, R. Protić, M. Šćepanović
Jao, jeste. Ta knjiga je blago rečeno užas. Zato sam ja radio „razumevanje“ iz skripata Pola Dokinsa: http://www.elitesecurity.org/p1486998[ Illiron @ 25.04.2009. 20:00 ] @
Citat: kingakul: sta to znaci kukam na rok? ne kukam ja nista nego kazem da na ETF-u znati logaritamski izvod vredi 4 poena od 100 (nakon sto si polozio eliminacioni) a npr. na fonu: http://mata.fon.rs/uploaded/mat1/pismeni/mm1_2008_feb.pdf
ima 4 zadataka jedan je limes koji se resava u 2-3 reda drugi funkcija koja se stvarno tesko ispituje.
samo sam hteo da opovrgnem to besmisleno napadanje kako je na ETF-u najlaksa matematika i kako je tu najveca kriza i degradacija. a na fonu ( na kome fon-ovci predaju matematiku) ocigledno moze gimnazijalac da polozi ispit bez spremanja ako je imao 4 ili 5 u prosecnoj gimnaziji. dakle manite se vise ETF-a ima vecih problema...
Svi predavači matematike na FON-u su matematičari.
[ petarm @ 07.11.2009. 16:22 ] @
Zanimljiva rasprava! Ja bih napisao nešto iz svog ugla. Rekao bih da bi matematičari koji predaju npr. fizičarima, inženjerima morali više da se prilagode studijima istih. Meni su matematičari predavali Matematičku analizu 1,2,3,4, Algebru, Numeričku matematiku, a fizicari Matematičku fiziku 1,2 i Matematičke metode kvantne fizike. Prednost poslednja 3 kursa je to što kada bismo videli neki metod rešavanja nečega rekli bi nam odmah i gde se to pojavljuje u fizici, što ima smisla. Mislim da su ti kursevi bili puno konkretniji, u smislu korisniji. Jako loše je što se na fizici cele prve godine ne radi samo matematika, pa da se od druge krene na fiziku. Jer ima puno praznog hoda. Već u prvom semestru prve godine fizičari pričaju linearne ODJ, neke elemente vektorske analize, koriste razvoj u red... Ali se na tome ne zadržavaju puno jer kažu to ćete raditi na matematici. A u okviru matematičke analize 1 krenemo sa nizovima, konvergencijom i završavamo je sa integralima. Neke stvari se ipak teško menjaju...
Ipak za neke stvari se na fizici u prvoj godini dobije lep osećaj. Sećam se jednog od prvih zadataka na vežbama iz mehanike sa prve godine.
ZAD
Po koordinatnim osama 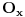 i 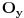 kreću se dve tačke  i  , koje su spojene štapom dužine  . Brzina tacke  je 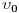 . Pri kakvom položaju tačaka će brzina tačke  biti 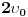 ?
REŠ
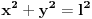
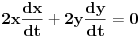
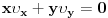
Odavde se dobije da je 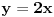 vrati se u 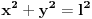 i dobije se položaj tačaka. Vrlo jednostavan zadatak, ali je jako dobar za početak jer daje neku sigurnost i osećaj jer se svaki složen zadatak sastoji iz više prostih!
Ne vidim prepreku na matematičari uzmu malo ovakve stvari, pogledaju i daju neki takav sličan primer na vežbama iz analize 1. Ali matematičari to obično izbegavaju, ne žele u to da ulaze da pogledaju i sl. Čast izuzecima! Kada bi ušli malo u ove vode i prilagodili se oni bi svakako to držali bolje od fizičara. Da kad krenu nešto da predaju probaju to da nađu u nekoj fizičarskoj knjizi i da daju primer gde se to pojavljuje i sl. Jer pređu dosta stvari koje posle fizičari ne koriste, a ne pređu ono što im treba i zbog toga mislim da bi bilo bolje efikasnije, pod uslovima koji su, da matematike drže teorijski fizičari na fizici. [ Nedeljko @ 07.11.2009. 17:14 ] @
Nisam siguran da si u pravu, jer na univerzitetima jačim od naših matematiku predaju matematičari.
Zamisli da te neko uči množenje brojeva koji imaju decimalni deo. Kad bi krenuo da tupi gde ti sve treba množenje, nigde ne bi stigao. Matematika je tu da kaže šta važi pod kojim uslovima. Univerzalna je u smislu da teoreme važe pri bilo kojoj interpretaciji polaznih pojmova u kojoj su zadovoljene sve aksiome. To joj omogućava primenu u drugim oblastima. Ja ne mogu da razumem metodologiju učenja tako što se rade zadaci bez teorisjkog minimuma. Ne znam kako bih mogao da rešavam zadatke iz nečega što ne razumem. Nije mi čudno ako studenti koji tako rade imaju problem sa prepoznavanjem tih aparata u primeni, jer ne sagledavaju značenje onoga što rade.
[ petarm @ 07.11.2009. 18:52 ] @
Citat: Nedeljko: Nisam siguran da si u pravu, jer na univerzitetima jačim od naših matematiku predaju matematičari.
Slažem se s tobom. Imaš na youtube-u kurs The Fourier Transforms and its Applications u Stanfordu za inženjere. Nekih 30 predavanja. Čovek ne priča teorema, dokaz... već daje puno primera i sl. Prilagodio je svoj kurs inženjerima. Osvrne se na neke probleme sa kojima će se susretati... Kod nas matematičar kome god da priča, priča na isti način. E to tako u svetu ne ide.
Citat: Nedeljko:
Zamisli da te neko uči množenje brojeva koji imaju decimalni deo. Kad bi krenuo da tupi gde ti sve treba množenje, nigde ne bi stigao. Matematika je tu da kaže šta važi pod kojim uslovima.
Množenje decimalnih brojeva ne spada u matematiku već u račun. S toga mislim da primer nije najbolji!
Citat: Nedeljko: Ja ne mogu da razumem metodologiju učenja tako što se rade zadaci bez teorisjkog minimuma.
Ne pričam ja da se ne radi teorija, već da se ta teorija prilagodi potrebama ljudi koji je slušaju.
[Ovu poruku je menjao petarm dana 07.11.2009. u 20:25 GMT+1]
[Ovu poruku je menjao petarm dana 07.11.2009. u 20:26 GMT+1][ Nedeljko @ 07.11.2009. 21:03 ] @
Ja sam množenje učio u osnovnoj školi iz predmeta matematika. Ako ćemo o tome šta je račun, po anglosaksoncima je calculus ono što se kod ans uči iz analize 1 i 2.
Što se nastave tiče, definicije i teoreme moraju da se rade, a dokazi se izostavljaju, sem ako ilustruju neku ideju. Manje dokaza, više vremena za primere. To nije tako samo na kursevima za inženjere, nego i za matematičare.
[ petarm @ 07.11.2009. 23:17 ] @
Citat: Nedeljko: Ja sam množenje učio u osnovnoj školi iz predmeta matematika.
Množenje te je učila učiteljica ili učitelj, dakle osoba koja nije matematičar, a predavala ti je matematiku i naučila te da množiš! :)
Mihail Talj je svojevremeno bio u Beogradu na tadašnjem PMF-u i bolje je množio brojeve od matematičara koji su mu stali na crtu, a završio je književnost! :)
Mislio sam na sledeću stvar. Radiš Gausovu teoremu. Ajmo primena Gausove teoreme u fizici. Prvo ti to odradi matematički, a onda daj primer primene toga u fizici. Recimo mi smo iz Analize 1 radili zadatke tipa pokazati po definiciji da je
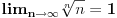
ili
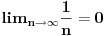
To fizičarima nije potrebno. To je gubljenje vremena! Citat: Nedeljko:
Što se nastave tiče, definicije i teoreme moraju da se rade, a dokazi se izostavljaju, sem ako ilustruju neku ideju. Manje dokaza, više vremena za primere. To nije tako samo na kursevima za inženjere, nego i za matematičare.
Sa ovim se slažem! Mada i sa brojem teorema i definicija ne treba preterivati!
Evo pogledaj npr. ovo predavanje fizičara sa Jejla.
http://www.youtube.com/watch?v...layList&p=FE3074A4CB751B2B
[Ovu poruku je menjao petarm dana 08.11.2009. u 01:12 GMT+1][ Nedeljko @ 08.11.2009. 09:43 ] @
Citat: petarm: Množenje te je učila učiteljica ili učitelj, dakle osoba koja nije matematičar, a predavala ti je matematiku i naučila te da množiš! :)
A ko je matematičar? Ja sam čuo mišljenja po kojima neki ljudi koji su se bavili matematikom iz hobija i dali vrhunske rezultate nisu matematičari!
No, to i dalje ne znači da to nije matematika.
To što je neko završio književnost ne znači da nema još neke skilove. BTW mislio sam da je bio elektroinženjer.
Ne znam na koju Gausovu teoremu misliš, ali primene u fizici će odraditi fizičari mnogo bolje. Matematičar treba da te obuči da prepoznaješ situacije gde se može upotrebiti i da umeš u njima da upotrebiš.
Što se limesa koje si naveo tiče, bitno je uvežbati neke tehnike, koje ti mogu koristiti. Ovde je reč o epsilon-delta računu. Možda je ovaj prvi limes preteran, ali onaj drugi i nešto složeniji od njega i divergencija niza (-1) n su svakako na mestu.
Ma, ni prvi nije težak. Razvija neku sposobnost mišljenja. Treba dokazati da niz 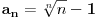 teži nuli. Jasno je da je to niz pozitivnih članova. Treba dokazati da je malo preko nule. Pa, 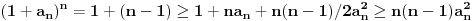 , pa je 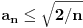 za 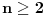 . Taj limes je kanije važan za druge limese, ali se slažem da je korisnije navesti ga kao činjenicu i kasnije koristiti.
Citat: petarm: Sa ovim se slažem! Mada i sa brojem teorema i definicija ne treba preterivati!
Izbor teorema i definicija je određen oblašću primene. [ petarm @ 08.11.2009. 10:28 ] @
Citat: Nedeljko: To što je neko završio književnost ne znači da nema još neke skilove. BTW mislio sam da je bio elektroinženjer.
Botvinik je bio elektroinženjer! 
Kažem nije loše uraditi jedan 2 primera, ali ne treba preterivati! Nađoh svesku pokazivano je još po definiciji
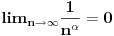 , 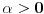
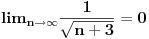
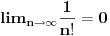
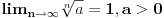
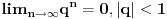
Ili rađen je npr. zadatak.
ZAD
Pokazati da  nije granična vrednost niza 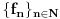 gde je 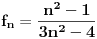 .
Ne kažem, ovo su jako zanimljivi zadačići, čak rekao bih zabavni!  I pružaju odreženi osećaj. Ali na kraju kursa, kad je došlo vreme za integrale bio je priličan cajtnot. Ne bih ja imao ništa protiv ovakvog načina rada da smo mi radili tu analizu 1 2 semestra kao matematičari, a to bi moglo jedino ako bi opšti kursevi fizike kretali od druge godine ili ako bi prvi kurs fizike bila recimo optika na prvoj godini. U suprotnom ovo raditi na fizici nije najbolje. Inače šta misliš o predavanju sa Jejla, ako si pogledao?
[ Nedeljko @ 08.11.2009. 12:04 ] @
Prvi limes raditi.
Drugi i treći za domaći.
Četvrti raditi ili preskočiti.
Peti za domaći.
Jedino što bih zamerio predavanju Tejlorovog reda je što nije dao nijedan dovoljan uslov kada se to može primeniti. Umereni primeri iz fizike (E)mc2) ubijaju dosadu kod studenata fizike i daju im neku motivaciju. Van toga ne vidim neku funkciju takvih primera, jer se te stvari ionako obrade mnogo bolje na kursevima fizike.
Recimo, video sam po kursevima one ocene ostatka, ali to nije uvek praktično, jer zahteva računanje n-tog izvoda funkcije. Funkcije koje se mogu u okolini bilo koje tačke domena razviti u Tejlorov red koji konvergira baš toj funkciji u nekoj okolini ke tačke. Dobro je dati neke praktične kriterijume kada je funkcija analitička.
Primera radi, ako je funkcija jednaka sumi stepenog reda, onda je ona analitička u unutrašnjosti oblasti konvergencije tog reda. Štaviše, ako je data kao suma stepenog reda u okolini tačke 0 sa poluprečnikom konvergencije 5, onda će Tejlorov razvoj iste funkcije u okolini tačke 4 imati poluprečnik konvergencije najmanje 1. Takođe, klasa analitičkih funkcija je zatvorena za sabiranje, oduzimanje, množenje, delenje, invertovanje, kompoziciju, pa su sve elementarne funkcije analitičke. No, ono što bi fizičarima moglo biti interesantno je pod kojim uslovima za diferencijalnu jednačinu u nekoj oblasti su njena rešenja u toj oblasti analitička. Takve stvari nisam našao nigde. Izgleda da toga nema ni na Jejlu.
[ petarm @ 08.11.2009. 14:26 ] @
Citat: Nedeljko:
Jedino što bih zamerio predavanju Tejlorovog reda je što nije dao nijedan dovoljan uslov kada se to može primeniti.
Ta zamerka stoji naravno! Ali ipak da je krenuo da priča o tome pitanje dokle bi stigao. Ima jedan duhovit deo kada kaže možemo isti razvoj koristi i za matrice
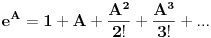
pa čak i za kućne ljubimce!  I naravno deljenje sa standardnim psom, npr. Napoleonovim psom... 
Osposobio ih je za neke stvari u kratkom vremenu. Npr. za 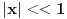 može se koristiti da je
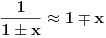 i njima je sad jasno odakle im se to pojavljuje! A ovakva ocena se često koristi u fizici.
Citat: Nedeljko:
Umereni primeri iz fizike (E)mc 2) ubijaju dosadu kod studenata fizike i daju im neku motivaciju. Van toga ne vidim neku funkciju takvih primera, jer se te stvari ionako obrade mnogo bolje na kursevima fizike.
Ja pričam o jednom drugom problemu. A to je da fizičari dok slučaju te matematičke predmete na prvoj godini imaju uporedo s njima Mehaniku i Termodinamiku. To je problem. Znači neće prvo odslušati taj kurs Analize 1 pa onda imati mehaniku već će to imati uporedo! Kasnije se to pegla.
[ Nedeljko @ 08.11.2009. 19:54 ] @
Koliko god da ovaj čovek priča fenomenalno, ja sam ga jedva slušao. Bio mi je ubistveno dosadan sa tim laganim tempom. No, to je na predavanju onima koji tu materiju ne znaju važno, da bi im ostavio vremena da shvate te pojmove. Čovek insistira na razumevanju problematike i to je skroz u redu. Međutim, da je napisao formule za procenu ostatka i dao par primera, ne smatram da bi izgubio mnogo vremena.
[ estamaster @ 23.07.2010. 14:16 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|