[ pjesce @ 20.11.2004. 17:21 ] @
| Da li bi neko mogao da mi objasni pojam ordinalnog broja malo elementarnije,ili da me uputi na neke korisne linkove iz teorije skupova? Pretraživao sam na wolframu,ali nije mi bas najjasnije. |
|
[ pjesce @ 20.11.2004. 17:21 ] @
[ Danica Porobic @ 20.11.2004. 21:38 ] @
Pogledaj ove skripte iz teorije skupova, u principu je objasnjeno na isti nacin kao i na mathworld-u, ali malo detaljnije i na srpskom ( ne znam da li ti ovo nesto znaci ):
http://www.im.ns.ac.yu/personal/madaraszr/Rozi-licno/skupovi.pdf [ darkosos @ 25.11.2004. 19:17 ] @
Ordinali služe za nabrajanje. Nešto kao generalizacija rednog broja. Evo šta kažu knjige:
- prvo pojam tranzitivnog skupa: skup x je tranzitivan ako 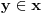 povlači povlači 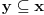 šta ovo znači? ako x sadrži neki skup, onda sadrži i sve njegove elemente; - onda se kaže da su ordinali tranzitivni skupovi koji su potpuno uređeni relacijom pripadanja; evo kako izgledaju (radi lakšeg zapisa a i kao potvrda intuicije, uvode se standardne oznake): 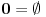 , , 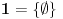 , , 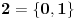 , , 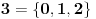 , ..., , ..., 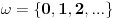 , , 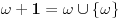 , ... , ...Poredak ordinala se uvodi sa 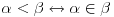 Kardinali su ordinali koji se ne mogu preslikati 1-1 u neki manji ordinal. Svi konačni ordinali su kardinali. [ Nedeljko @ 26.11.2004. 01:40 ] @
[ klupko @ 27.11.2004. 16:39 ] @
http://mapmf.pmfst.hr/~matko1/teorijaskupovateheksplorer.pdf
u poglavlju (mislim cetvrtom) o dobro uredjenim skupovima. [ darkosos @ 27.11.2004. 19:12 ] @
Hm, interesantno. Kakav je značaj ordinalnih skupova u aksiomatici bez aksiome regularnosti? I kako se to odražava na pojam kardinalnog broja; ili na primer na hipotezu kontinuuma? I baš me zanima koje su to aktuelne teorije skupova bez aksiome regularnosti? Već smo ovde na forumu imali neku raspravicu o njenom značaju.
[ Nedeljko @ 27.11.2004. 19:47 ] @
Ordinalni brojevi se mogu uvesti na više načina. U literaturi je prihvaćen ovaj Fon Nojmanov kao tranzitivnih skupova dobro uređenih relacijom
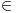 kao relacijom strogog poretka. Me]utim, pošto oni služe za nabrajanje (kao što si već napisao), suštin aim je u tome da se svaki skup može 1-1 preslikati u klasu svih ordinala (tj. ne postoji skup svih ordinala), da su dobro uređeni na neki način, i da za svaki ordinal kao relacijom strogog poretka. Me]utim, pošto oni služe za nabrajanje (kao što si već napisao), suštin aim je u tome da se svaki skup može 1-1 preslikati u klasu svih ordinala (tj. ne postoji skup svih ordinala), da su dobro uređeni na neki način, i da za svaki ordinal  postoji skup svih ordinala koji su manji od postoji skup svih ordinala koji su manji od  u tom uređenju. u tom uređenju.Zato se njihova dobra uređenost uzima kao njihovo osnovno svojstvo (jer odražava njihovu suštinu), a onda se navode ekvivalentni uslovi. Ovaj sa linearnošću je važan kod modela Teorije Skupova, jer se na taj način dokazuje da je osobina "biti ordinal" apsolutna za sve tranzitivne modele. Inače, aksioma regularnosti važi u svm tranzitivnim mkdelima. Ipak, zbog prethodne primedbe takav način definisanja nije zgodan za nekoga ko prvi put uči Teoriju Skupova. Teorija skupova bez aksiome regularnosti ima koliko i teorija skupova sa regularnošću. Radi se samo o tome da li je ta aksioma u spisku izabranih aksioma ili ne. [ pjesce @ 28.11.2004. 15:36 ] @
Moram zaista svima da se zahvalim na pomoći;dobio sam par korisnih linkova i iscrpnih saveta,tako da mogu da nastavim svoj voyage kroz teoriju skupova.Takodje,nadam se da ću i ja biti u prilici da nekome nesebično pomognem kao i vi meni.Bravo za forum!!!
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|