[ kajla @ 05.04.2002. 16:05 ] @
| Da li neko zna gde mogu naći formaluciju i dokaz ove teoreme. poz. |
|
[ kajla @ 05.04.2002. 16:05 ] @
[ StratOS @ 17.04.2002. 08:36 ] @
Kako se on originalno naziva ??
[ kajla @ 17.04.2002. 12:16 ] @
Na engleskom:
Muirhead's Theorem poz. [ alex @ 17.04.2002. 12:23 ] @
Probaj na Google-u. U ovom slucaju:
http://www.google.com/search?q=Muirhead%27s+Theorem Bojan Bašić: Čišćenje teme od flame-a [Ovu poruku je menjao Bojan Basic dana 16.11.2004. u 18:50 GMT+1] [ kajla @ 17.04.2002. 12:29 ] @
Fora je u tome što sam tražio i preko Google, AltaViste...ali nisam našao. Na jednom mestu sam našao formulaciju teoreme ali nigde dokaz i primere gde može da se upotrebi.
poz. Bojan Bašić: Čišćenje teme od flame-a [Ovu poruku je menjao Bojan Basic dana 16.11.2004. u 18:51 GMT+1] [ StratOS @ 17.04.2002. 12:47 ] @
Evo ti male literaturice, a što se tiče WEB searchera s pravim searchem se sve nađe !!!!
S. Dvoryaninov, E. Yasinovyi; Obtaining symmetric inequalities, Quantum (Nov. Dec. 1999) 44-48. - Muirhead's theorem (1903) by examples. (AG3) via Muirhead: Primjer: 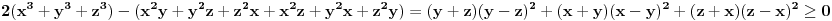 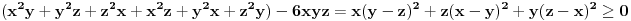 and therefore 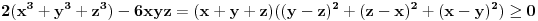 Bojan Bašić: tex [Ovu poruku je menjao Bojan Basic dana 16.11.2004. u 18:57 GMT+1] [ alex @ 17.04.2002. 12:53 ] @
Citat: Fora je u tome što sam tražio i preko Google, AltaViste...ali nisam našao. Na jednom mestu sam našao formulaciju teoreme ali nigde dokaz i primere gde može da se upotrebi! Na linku koji sam ti poslao sve sto ti treba moze bez problema da se nadje. Pozdrav, alex. Bojan Bašić: Čišćenje teme od flame-a [Ovu poruku je menjao Bojan Basic dana 16.11.2004. u 18:51 GMT+1] [ kajla @ 18.04.2002. 16:18 ] @
Kliknuo sam na link koji si poslao i nisam našao nikakve primere niti dokaz za Muirheads theorem.
poz. Bojan Bašić: Čišćenje teme od flame-a [Ovu poruku je menjao Bojan Basic dana 16.11.2004. u 18:52 GMT+1] [ alex @ 18.04.2002. 16:25 ] @
Tamo ima nekoliko PDF dokumenata sa bas tim - izvodom teoreme i dokazom..
alex. Bojan Bašić: Čišćenje teme od flame-a [Ovu poruku je menjao Bojan Basic dana 16.11.2004. u 18:52 GMT+1] [ kajla @ 25.04.2002. 01:09 ] @
Ajde molim te alex daj mi adrese ti .pdf u kojima se nalazi formulacija, dokaz kao i primeri vezani za Muirhedovu teoremu, da ne bude da ja izmišljam.
poz. Bojan Bašić: Čišćenje teme od flame-a [Ovu poruku je menjao Bojan Basic dana 16.11.2004. u 18:53 GMT+1] [ kajla @ 01.05.2002. 00:12 ] @
Ajde sad alex priznaj da si pogrešio...
poz. [ Metalnem @ 26.02.2005. 17:56 ] @
Imam tri pitanja u vezi Mjurhedove nejednakosti:
1) Da li je ovo tacna formulacija nejednakosti: Ako su 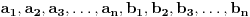 celi brojevi takvi da je celi brojevi takvi da je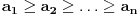 , , 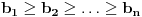 , , 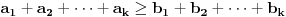 , , 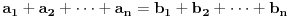 i i 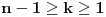 onda vazi: onda vazi: 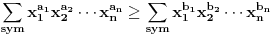 za svako za svako 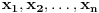 u skupu pozitivnih realnih brojeva. u skupu pozitivnih realnih brojeva.2) Da li je ispravan nacin resavanja sledeceg zadatka? Dokazati da je za pozitivne brojeve a, b i c zadovoljena nejednakost 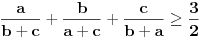 . .Pomnozimo obe strane nejednakosti sa 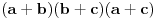 . Posle svih mnozenja i sredjivanja dobijamo . Posle svih mnozenja i sredjivanja dobijamo 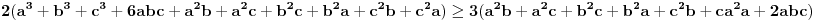 sto mozemo zapisati kao sto mozemo zapisati kao 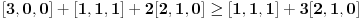 sto je po Mjurhedovoj nejednakosti tacno. sto je po Mjurhedovoj nejednakosti tacno.3) Da li neko moze da postavi ovde nekoliko primera u kojima se moze iskoristiti Mjurhedova nejednakost? [ Nedeljko @ 26.02.2005. 18:36 ] @
Na prva dva pitanja je odgovor pozitivan, s tim da u iskazu teoreme važi ekvivalencija. Teorema još tvrdi da se u tom slučaju jednakost dostiže ako i samo ako su svi ti pozitivni realni brojevi jednaki. Takođe, izložioci mogu biti bilo koji nenegativni realni brojevi.
[ Bojan Basic @ 26.02.2005. 19:54 ] @
Nedeljko ti je u principu odgovorio, samo bih ga malo dopunio.
1) Zaboravio si da napomeneš da su svi a-ovi i b-ovi pozitivni; 2) Način koji si predložio za rešavanje ovog zadatka je dobar s tim što moram da napomenem da ako budeš sličan zadatak rešavao "zvanično" (na nekom kontrolnom ispitu, takmičenju...) kreni suprotnim redosledom od ovog koji si ti naveo, tj. napišeš: "Na osnovu Mjurhedove nejednakosti imamo da je 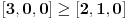 iz čega sledi...". Ovo pričam zbog toga što znam da ti što pregledaju takve stvari vole da zakinu bodove što nisi svugde pisao ekvivalenciju, u principu to ne bi smeli da rade ali ništa te ne košta da napišeš ovako kao što sam rekao. Znači, sebi sa strane skiciraš rešenje, vidiš šta se dobije na kraju, i onda na onom listu što predaješ kreneš odatle pa stigneš do početka, ako razumeš šta hoću da kažem. iz čega sledi...". Ovo pričam zbog toga što znam da ti što pregledaju takve stvari vole da zakinu bodove što nisi svugde pisao ekvivalenciju, u principu to ne bi smeli da rade ali ništa te ne košta da napišeš ovako kao što sam rekao. Znači, sebi sa strane skiciraš rešenje, vidiš šta se dobije na kraju, i onda na onom listu što predaješ kreneš odatle pa stigneš do početka, ako razumeš šta hoću da kažem.3) Možeš da rešiš 95% nejednakosti gde su promenjive ravnopravne, Mjurhed je zakon za takve stvari (iako u 90% slučajeva postoji jednostavnije rešenje primenom AG ili neke slične manje moćne nejednakosti zahvaljujući Mjurhedu uopšte ne moraš da razmišljaš šta sa čim kombinovati, samo izmnožiš sve, poskraćuješ šta možeš i vidiš šta ostaje na kraju). Evo i par primera koji su mi trenutno pali pod ruku (neki mogu i sasvim elementarno ali napisaću ih ovde radi ilustracije Mjurhedove nejednakosti): I) http://www.elitesecurity.org/tema/98452 (pošto si ti postavio temu sigurno znaš za ovo, ali neka stoji ovde da i drugi korisnici mogu da vide); II) Ako su 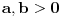 , , 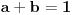 , dokazati , dokazati 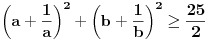 . .III) Za 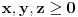 , , 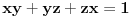 dokazati da važi dokazati da važi 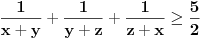 . .IV) Ako 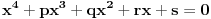 ima 4 realna pozitivna rešenja, dokazati da važi: ima 4 realna pozitivna rešenja, dokazati da važi:a) 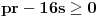 ; ;b) 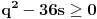 . .Mislim da je dosta za sada. [Ovu poruku je menjao Bojan Basic dana 27.02.2005. u 15:47 GMT+1] [ Nedeljko @ 26.02.2005. 22:08 ] @
Bojane, napisao sam da izložioci (ili što ti kažeš a-ovi i b-ovi) moraju biti nenegativni realni brojevi.
[ Bojan Basic @ 26.02.2005. 22:15 ] @
Da, napisao si, sorry.
[ Metalnem @ 27.02.2005. 13:03 ] @
[ Bojan Basic @ 27.02.2005. 14:48 ] @
U pravu si, postojala je sitna greška u trećem zadatku (sad je ispravljena), međutim nažalost formulaciju Mjurhedove nejednakosti smo pisali iz više delova pa dopunjavali par puta tako da je na kraju nastala prava papazjanija, i preskočen je važan detalj. Zbog toga pišem sve ispočetka kako bismo imali na jednom mestu a ne iscepkano u više poruka:
FORMULACIJA MJURHEDOVE NEJEDNAKOSTI Neka su  i i 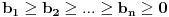 realni brojevi takvi da je realni brojevi takvi da je 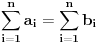 . Akko je: . Akko je: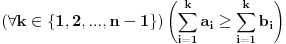 onda za sve nenegativne realne brojeve 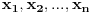 važi: važi: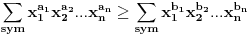 Napomena: Iako je 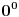 u matematici neodređen izraz u ovom slučaju se pretpostavlja da je u matematici neodređen izraz u ovom slučaju se pretpostavlja da je 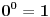 , što donekle ima smisla jer znamo da važi , što donekle ima smisla jer znamo da važi 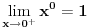 . Slažem se da ovo nije baš najsretnije rešenje i zbog toga se često Mjurhedova nejednakost citira samo za pozitivne brojeve, ali ovo je generalni oblik i treba ga prihvatiti. . Slažem se da ovo nije baš najsretnije rešenje i zbog toga se često Mjurhedova nejednakost citira samo za pozitivne brojeve, ali ovo je generalni oblik i treba ga prihvatiti.Jednakost važi ako su svi brojevi međusobno jednaki, ali ne možemo staviti ekvivalenciju jer se može dogoditi da je jednakost ispunjena ako su neki od brojeva jednaki  . Međutim, ako se ipak odlučimo da Mjurhedovu nejednakost ograničimo samo na pozitivne brojeve, u tom slučaju jednakost važi ako i samo ako su svi brojevi međusobno jednaki. . Međutim, ako se ipak odlučimo da Mjurhedovu nejednakost ograničimo samo na pozitivne brojeve, u tom slučaju jednakost važi ako i samo ako su svi brojevi međusobno jednaki.[Ovu poruku je menjao Bojan Basic dana 01.03.2005. u 22:57 GMT+1] [ Nedeljko @ 27.02.2005. 15:15 ] @
Pomenuti izraz nema definisanu vrednost u matematici jer ne postoji limes od xiy kada x teži nuli sa desne strane i y teži nuli na proizvoljan način. Ipak, to ne znači da nema smisla u konkretnoj situaciji uzeti da taj izraz ima određenu definisanu vrednost. Bitno je da se zna sadržaj teoreme, kao i da postoji dokaz iste u toj formulaciji. Nije ništa pogrešno u iskazu teoreme uzeti tako nešto po konvenciji (samo za iskaz teoreme i njen dokaz). Štaviše u teoriji skupova u kardinalnoj, kao i ordinalnoj aritmetici jeste 00=1. Često se i u aritmetici prirodnih, celih i racionalnih brojeva (dakle u teoriji brojeva), kao i u algebri (odnosno gde nemamo posla sa limesima) vrednost tog izraza uzima baš tako. U teoriji mere i integracije je na primer nula puta beskonačno jednako nuli.
Međutim, u toj formulaciji Mjurhedove teoreme je potreban i dovoljan uslov da važi jednakost da su svi članovi koji su različiti od nule međusobno jednaki. [ Bojan Basic @ 27.02.2005. 16:23 ] @
Citat: Nedeljko: Međutim, u toj formulaciji Mjurhedove teoreme je potreban i dovoljan uslov da važi jednakost da su svi članovi koji su različiti od nule međusobno jednaki. Ovo je i meni palo na pamet u jednom momentu, ali ipak nije tačno, pogledaj najjednostavniji primer: 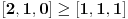 Sad tražimo kad važi jednakost. Uzmimo da je  , , 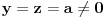 , ali jednakost i dalje nije zadovoljena: , ali jednakost i dalje nije zadovoljena: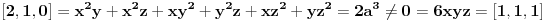 Evo i drugačijeg primera, u ovom slučaju uzmimo da je  , , 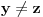 a jednakost ipak može da bude ispunjena: a jednakost ipak može da bude ispunjena: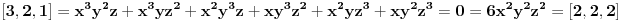 Sve u svemu, mislim da bi generalno trebalo razmatrati nekoliko posebnih slučajeva tako da je bolje da ne dajemo neku opštu definiciju već da ostavimo da se procenjuje na osnovu konkretnog zadatka. [ Nedeljko @ 27.02.2005. 21:38 ] @
Tako mi i treba kada brzopleto dajem izjave.
[ Bojan Basic @ 27.02.2005. 21:47 ] @
Nemoj da se nerviraš, svi grešimo, zato i postoji ovaj forum da možemo razmeniti mišljenja i eventualno jedni drugima skrenuti pažnju na grešku ako se ukaže potreba za tim.
[ Nedeljko @ 28.02.2005. 00:15 ] @
Ne nerviram se ni najmanje. Samo sam mogao da proverim tvrdnju pre nego što je napišem.
[ Metalnem @ 28.02.2005. 14:22 ] @
Da li se zadatak III moze resavati na sledeci nacin: prvo se pomoze obe strane sa 2(x+z)(x+y)(y+z) i na levoj strani se dobija da je zbir izlozilaca u svim sabircima 2, a na desnoj 3. Zatim sve to kvadriramo, pa levu stranu pomnozimo sa xy+xz+yz. Dobijamo i na levoj i na desnoj strani da je zbir izlozilaca u svim sabircima 6 i onda od toga napravimo nejednakost?
PS: Za ovo sto sam napisao mislim da je x, y ,z > 0. Slucaj kada je jedan od brojeva jednak nuli se lako dokazuje. [ Bojan Basic @ 28.02.2005. 19:52 ] @
Citat: Metalnem: Da li se zadatak III moze resavati na sledeci nacin: prvo se pomoze obe strane sa 2(x+z)(x+y)(y+z) i na levoj strani se dobija da je zbir izlozilaca u svim sabircima 2, a na desnoj 3. Zatim sve to kvadriramo, pa levu stranu pomnozimo sa xy+xz+yz. Može, naravno. U sličnim zadacima se često koristi sličan trik kao u zadatku I gde uvedeš nova slova da bi smanjio stepen onoga sa čime množiš (u tom slučaju bi uštedeo kvadriranje onolikog izraza što nije naročito zahvalan posao), međutim to ovde ne može da prođe tako da mora ovako. Reci mi samo zašto bi hteo da posebno ispituješ slučaj kada je neki od brojeva jednak 0 jer je to sve obuhvaćeno Mjurhedovom nejednakosti. Što se tiče ovog tvog zadatka nisam siguran da li si ga postavio kao primer ili zato što ti treba rešenje, ali u svakom slučaju i on ide trivijalno, kreneš od 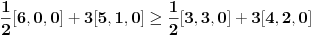 (što je tačno), a to upravo predstavlja razvijeni oblik tvog izraza. (što je tačno), a to upravo predstavlja razvijeni oblik tvog izraza.[ Metalnem @ 28.02.2005. 20:38 ] @
Citat: Reci mi samo zašto bi hteo da posebno ispituješ slučaj kada je neki od brojeva jednak 0 jer je to sve obuhvaćeno Mjurhedovom nejednakosti. Da, izvinjavam se, nisam pazljivo procitao jedan od tvojih ranijih postova. A ovaj zadatak je cisto kao primer ako jos nekoga interesuje. [ useer @ 21.06.2006. 18:29 ] @
iz ovih vasih postova i naravno neke literature sa neta naucio sam mjurheda i sad sam malo pokusavao da ga navezbam i to ide malo po malo ali sve na nekim tezim zadacima...imate li neke zadatke za mjurheda (i ostale teoreme iz nejednakoti)na kojima bih mogao da steknem osecaj za to da bih posle mogao da radim i teze stvari
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|