Matrica A:

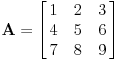Determinanta matrice A: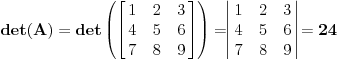


Matrica ti je, prostim rečima tabela od n vrsta i m kolona koja sadrži neke brojeve (ima i drugih matrica, ali da te ne zamaram). Dakle skup nekih elemenata, najčešće brojeva.

Sa druge strane, determinanta je brojevna karakteristika matrice. Determinantu neke matrice je moguće odrediti samo ako je ta matrica kvadratna (n=m). Nemoj da te buni to što se prikazuje kao matrica. Determinanta je samo jedan broj (u slučaju ove matrice je 24). Možeš na determinantu da gledaš kao na preslikavanje iz skupa matrica u skup (realnih) brojeva - funkcija koja za datu matricu daje neki realan broj.


Matrice i determinante imaju veoma široku primenu, i bilo bi uzaludno nabrajati sve. Recimo da su matrice veoma korisno oruđe pri rešavanju sistema linearnih jednačina, zatim kod nekih 3D transformacija objekata, itd...
Recimo na primer i to da kvadratna matrica ima svoju inverznu matricu ako i samo ako je determinanta te matrice različita od nule.

Skup je potpuno određen svojim elementima. redosled i ponavljanja su nebitni. Međutim, kod matrica je raspored elemenata bitan. Stoga si pogrešno uportrebio reč skup. Dake, bolje tabela. Sve ostalo je OK.

I stand corrected.
Iskorisio sam izraz u kontekstu koji je matematički netačan. Hteo sam samo prostim rečima da objasnim pojam matrice.

Rekao bih da bi trebalo reci preslikavanje iz skupa matrica u skup kompleksnih brojeva!

DEterminanta je preslikavanje iy skupa kvadratnih matrica nad komutativnim prstenom K u taj komutativni prsten.