[ nnn @ 16.12.2004. 20:47 ] @
| Imam jedno pitanje: Kako se racunaju trigonometrijske funkcije bez pomoci tablica, digitrona...? Lupim neki ugao naprimer 32, kako cu dobiti njegov sinus ili tangens. |
|
[ nnn @ 16.12.2004. 20:47 ] @
[ zzzz @ 16.12.2004. 21:17 ] @
Pa na isti način na koji su Brigs i saradnici računali one silne brojeve
u tablicama.Ili radi po algoritmu koji je ugrađen u kalkulator što je u suštini isto.Šalim se.Postoje tzv.Tejlorovi redovi u koje se mogu te funkcije zgodno razviti,a onda idu samo algebarske operacije.Očito nisi jiš stigao do tog. [ Bojan Basic @ 17.12.2004. 10:27 ] @
Ako ti treba za neki ugao koji je blizu nekog "specijalnog" ugla (tj. kojeg možeš da izračunaš), npr. baš za ova 32o koje si pomenuo, možeš da zameniš priraštaj funkcije diferencijalom i tako ćeš dobiti prilično tačnu vrednost.
[ MAD-MAX @ 18.12.2004. 00:37 ] @
Ajde ako ti nije tesko postuj postupak i resenje. Bas bi mi dobro doslo.
[ Bojan Basic @ 18.12.2004. 13:27 ] @
[ zzzz @ 18.12.2004. 14:26 ] @
A evo i onog Tejlora (ili Mc Lorena?) po kojem su nekad oni jadni
ljudi danima strpljivo pravili tablice vrijednosti trig.funkcija. 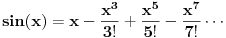 Sada ručno izračunavam član po član:x=32*pi/180=0.5585.(u rad.) Drugi član je -0.0290 Treći član je +o.ooo4 Suma je 0.5295.Napravio sam grešku od 0.003 jer sam radio sa premalo decimala.A i stao sam već kod trećeg člana. [ Nikola 23 @ 15.06.2010. 22:12 ] @
A moze li se to resiti nakako preko trigonometrijskog kruga, odnosno kada sestarom nacrtamo trigonometrijski krug.
Uz pomoc sestara, lenjira, uglomera,... [ Sini82 @ 16.06.2010. 12:56 ] @
Moze. Predstaviš ugao na trigonometrijskoj kružnici i izmjeriš "dužinu sinusa".
[ Fitopatolog @ 16.06.2010. 14:47 ] @
[ Cabo @ 16.06.2010. 16:26 ] @
Ispravljeno, hvala.
[ Nikola 23 @ 16.06.2010. 20:05 ] @
Bojane, a odakle si uzeo to pi/90 i dali to vazi u svakom slucaju ili samo u ovom?
[ Cabo @ 16.06.2010. 21:02 ] @
[ holononi @ 17.06.2010. 10:47 ] @
I tako smo dobili
[°] = [] [ zzzz @ 17.06.2010. 12:30 ] @
Citat: Niti je jasno niti je tako.Jedinica za mjerenje nije broj kako je gore napisano. Da bi nešto mjerili treba definisati jedinicu za mjerenje. Stepeni i radijani (a i gradi) su jedinice za mjerenje ugla,ali različite. Definicija prve jedinice:360-ti dio punog ugla. Definicija druge jedinice je:To je ugao kome je dužina luka jednaka radijusu tog luka.Ili to je 2pi-ti dio punog ugla. Definicija treće jedinice je:400 ti dio punog ugla. Međusobni odnos jedinica se računa preko punog ugla. Ima i drugih jedinica za mjerenje uglova koje se koriste.Naprimjer u artiljeriji imamo 1 hiljadita=ugao trokuta kome su katete 1 i 1000. Mogu se izmisliti i neke nove ako se ukaže praktična potreba. [ Nedeljko @ 17.06.2010. 13:10 ] @
OK, imaš 7 osnovnih SI mernih jedinica, metar, kilogram, sekund, kelvin, amper, mol i kandelu. Definiši mi radijan preko njih.
Dakle, 1 radijan = x masbkgcKdAemolfcdg. x je broj. [ Fitopatolog @ 17.06.2010. 13:12 ] @
Nedeljko, da li si prolupao na ovolikoj vrućini?
[ Nedeljko @ 17.06.2010. 13:22 ] @
Biće da je tebe ujela neka muva sa kravoj.
Kada budete izrazili radijan i stepen preko 7 osnovnih SI mernih jedinica, biće vam jasno šta su stepen i radijan. [ Fitopatolog @ 17.06.2010. 13:28 ] @
Vrlo slikovito si se izrazio - od muve si napravio KRAVU (t.j. slona). Ni jednostavnijeg pitanja - ni komplikovanijeg odgovora.
[ Nedeljko @ 17.06.2010. 13:46 ] @
U nedostatku boljih argumenata, prešao si na ad hominem i to zoveš jednostavnim pitanjem (koje uopšte nije pitanje).
[ Fitopatolog @ 17.06.2010. 13:54 ] @
Još je manje tvoj odgovor - odgovor. Mislim da "ovlaš", t j. površno pročitaš temu (kao u slučaju teme http://www.elitesecurity.org/t...lucaj-sa-imaginarnom-jedinicom kada si tek pred kraj teme pitao "O čemu se radi?") pa odatle nastane problem.
[ Fitopatolog @ 17.06.2010. 14:13 ] @
Nedeljko, da li stvarno ne znaš da izraziš radijan preko
Citat: ili nas zavitlavaš? [ Nedeljko @ 17.06.2010. 14:48 ] @
Naravno da znam. Nigde nisam napisao da ne znam, ali biće da ima onih koji ne znaju.
[ holononi @ 17.06.2010. 15:30 ] @
@Fitopatolog
Refernciaro si pravi problem jer i ovde je suština u frazi "zamena za". Inače radijan je odnos dužina te je broj rad = [m]/[m] = [] i nema jedinice mere. Stepen je (danas diskriminsana) jedinica mere pa je znak jednakosti problematičan ali se koristi uz dobro poznatu primedbu "bez opasnosti od zabune". Rešenje Nedeljkovog problema x * masbkgcKdAemolfcdg == x * 1 se može dobiti masbkgcKdAemolfcdg == 1 a=b=c=d=e=f=g=0 Ovakvo rešenje je dozvoljeno u matematici ali u stvarnosti nije realno. Rezultat matematičkih operacija nad mernim jedinicama je jednak 1 samo ako se merne jedinice "skraćuju", na primer [kg/kg] = 1 (neimenovan broj) [Ovu poruku je menjao holononi dana 17.06.2010. u 16:54 GMT+1] [ Cabo @ 17.06.2010. 15:33 ] @
What da ph***?
Jel se vi to malo bavite čamcima, a? x.O Evo šta kaže Vikipedija: http://en.wikipedia.org/wiki/Radian Citat: The radian is the standard unit of angular measure, used in many areas of mathematics. It describes the plane angle subtended by a circular arc as the length of the arc divided by the radius of the arc. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit. The SI unit of solid angle measurement is the steradian. [...] Conversion between radians and degrees A chart to convert between degrees and radians As stated, one radian is equal to 180/π degrees. Thus, to convert from radians to degrees, multiply by 180/π. 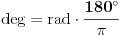 For example: 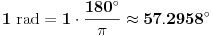 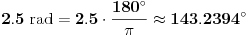 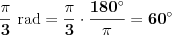 Conversely, to convert from degrees to radians, multiply by π/180. [ holononi @ 17.06.2010. 15:55 ] @
Šta si hteo da kažeš?
[ Cabo @ 17.06.2010. 15:58 ] @
Odgovaram Neđi.
[ Nedeljko @ 17.06.2010. 16:18 ] @
Citat: Cabo: the radian is now considered a SI derived unit Odlično! Definiši ga preko osnovnih SI jedinica. [ Cabo @ 17.06.2010. 16:23 ] @
Citat: One radian is the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle. More generally, the magnitude in radians of such a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, θ = s /r, where θ is the subtended angle in radians, s is arc length, and r is radius. Conversely, the length of the enclosed arc is equal to the radius multiplied by the magnitude of the angle in radians; that is, s = rθ. It follows that the magnitude in radians of one complete revolution (360 degrees) is the length of the entire circumference divided by the radius, or 2πr /r, or 2π. Thus 2π radians is equal to 360 degrees, meaning that one radian is equal to 180/π degrees. ... [ Nedeljko @ 17.06.2010. 16:26 ] @
Ja sam pitao za definiciju preko ostalih SI jedinica.
Ako to ne razumeš, jesi li položio osnove geometrije? Kako se tamo definiše mera ugla? [ holononi @ 17.06.2010. 17:28 ] @
Mera ugla (merni broj ugla) može da se definiše na različite načine. Ali time još nije definisan radijan. Te definicije kod nas obično su plod demonstracije sile, dok je definicija radijana data medjunarodnom konvencijom i tu nema zabune, trikova i nadmudrivanja, radijan je izvedena jedinica i predstavlja odnos dužina, [m/m] = 1.
Ako bi ste pošli od definicije date u knjizi M.Mateljević "Kompleksne funkcije 1&2" tada je "merni broj ugla" dužina luka, sledi jedinica mere za "merni broj ugla" je jedinica mere za dužinu a to je metar, što nikako nije radijan jer radijan nije metar ni bilo koji deo metra. U knjizi Z.Lučić "Euklidska i hiperbolička geometrija" mera ugla je data kao apstraktna mera i dobro je definisana. Medjutim ni ovde nije definisan radijan. I tako studenti završe fakultet a da nikad ne čuju pravu definiciju pojma koji redovno koriste. [ Sini82 @ 17.06.2010. 18:16 ] @
Krenimo od srednjoškolske definicije:
Citat: 1 radijan je mjera ugla kojem odgovara luk dužine 1 na kružnici poluprečnika 1. Nije tačno da je rad [m]/[m], odakle vam samo to? Stepen je stepen; radijan je radijan. 1 stepen=pi/180 rad i 1 rad=180 stepeni/pi (kao što je, lupam, 1 ar =100 m i 1 m=0.01 ara). U knjizi od Mateljevića piše: Citat: ...Ako luk l(...) pripada uglu, merni broj ugla (...) je dužina ovog luka (luka koji je presek ugla sa jediničnom kružnicom T);... Nigdje se ne spominje radijan. Merni broj nema jedinicu. U osnovama geometrije nigdje se ne uči da je radijan odnos dužina. Da dopunim svoj prethodni post u ovoj temi: 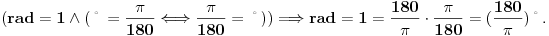 [ holononi @ 17.06.2010. 18:52 ] @
Citat: Nije tačno da je rad [m]/[m], odakle vam samo to? Iz medjunarodnog mernog sistema. Tamo su definisane SI merne jedinice i izvedene SI merne jedinice, radijan je izvedena merna jedinica data tako kako sam napisao, odnos dužina. Citat: Nigdje se ne spominje radijan. Merni broj nema jedinicu. Nisam ni napisao da se radijan spominje. Tačno je da merni broj nema jedinicu ali neki izgleda ne znaju da dužina ima jedinicu mere. I to je problem, u jednoj rečenici brkaju se dva pojma. Sve to šalje loše poruke studentima. Kako da neko ko je diplomirao učeći iz takvih knjiga posle može da daje srednješkolske definicije? Citat: U osnovama geometrije nigdje se ne uči da je radijan odnos dužina. Ne uči se... to se nauči u srednjoj školi :) [ Cabo @ 17.06.2010. 19:50 ] @
Citat: Nedeljko: jesi li položio osnove geometrije? Jesam, fala na pitanju. Mnogo cepidlačiš i teraš mak na konac. Radijan je radijan. Što praviti od komarca magarca? :-/ [ galet@world @ 17.06.2010. 21:16 ] @
Ovo je više nego smešno.
Radijan je ugao određene veličine, a to što se on dobija kao odnos dveju dužina je samo pomoćna stvar pomoću koje određujemo koliki je taj ugao. Odnos dveju dužina nije ugao - to je samo način na koji saznajemo koliki je taj ugao i kako ga možemo dobiti iliti to je postupak kojim određujemo veličinu tog ugla ali nije ugao. Ugao je pojava za sebe i ima dimenziju ugla, a njegova veličina, (a ne dimenzija koja ga definiše kao pojavu) se određuje radijanima, stepenima ili kako se već dogovori. Jedno je pojava, a drugo je količina ili veličina (deo) te pojave koju uzimamo kao jediničnu odnosno uporednu. [ Fitopatolog @ 17.06.2010. 21:25 ] @
Šta tek (na ovoj vrućini!) da se kaže za steradijan !?
[ galet@world @ 17.06.2010. 21:40 ] @
Isto!
[ holononi @ 17.06.2010. 21:45 ] @
Radijan je bezdimenziona mera, odnosno dimenzija 1 a skraćenica rad upravo označava tu 1. Ovo je medjinarodna konvencija i mora se poštovati. Predvidjene su i zakonske sankcije u slučaju ne poštovanja SI sistema mera. Mera ugla u radijanima je definisana kao odnos dužine luka i poluprečnika kruga. Jedan radijan je mera ugla koji odgovara luku dužine poluprečnika kruga. Moguće je da ima onih koji bi da uvedu "još bolje definicije" ali medjunarodni standardi se ne mogu menjati na forumima a pogotovu ne u nastavi.
A za steradijan slično, samo što je [m2/m2] i opet 1 ali sada sr, skraćenica od steradijan. [ galet@world @ 17.06.2010. 23:58 ] @
Meriti se može sve sa dogovorenim delom toga istog
Radijanom se određuje veličina mernog dela uglova i on je ugao Ako je radijan odnos dveju dužina onda on nije ugao jer nema dimenziju ugla nego odnosom dveju dužina određuje se veličina ugla koji će služiti kao mera Svi nazivi mera određuju veličinu (količinu) neke pojave, a ne definišu je Put može da se meri metrom, ali metar i put imaju istu dimenziju (dimenziju dužine) Ako se podeli put sa metrom dobijamo rezultat bez dimenzije koji označava količinu Ako neku masu podelimo sa kilogramom rezultat je bez dimenzije koji označava količinu i tako je uvek Ako merenu količinu podelimo sa merom rezultat je bez dimenzije i označava količinu mernih jedinica Ako neki ugao podelimo sa radijanom rezultat mora biti bez dimenzije jer je i radijan ugao i rezultat je bez dimenzije i označava količinu takvih mernih uglova - rezultat nije ugao nego količina. ali... ako neki ugao podelimo sa brojem bez dimenzije rezultat nije bez dimenzije i ne pretstavlja količinu već pretstavlja deo tog ugla koji je takođe ugao. [ zzzz @ 18.06.2010. 01:28 ] @
Citat: Nedeljko: Ja sam pitao za definiciju preko ostalih SI jedinica. Ako to ne razumeš, jesi li položio osnove geometrije? Kako se tamo definiše mera ugla? Fizika i matematika nisu isto.SI sistem mjera vrijedi samo za dio fizke koji se zove tehnički dio a obavezno se koristi samo u javnoj upotrebi.To je propisano zakonom. Matematika je apstraktna pa nema takve obaveze.Ali ipak u geometriji imamo potrebu za definicijom jedinice dužine i ugla. Pomoću duži l= jedan koju slobodno definišemoi možemo naprimjer nacrtati trokut sa stranicama 2,7,9.I odatle naprimjer naći prečnik opisanog kruga.Svako od nas će to ispravno riješiti i napisati koliko je R iako su nam jedinice duži različite u odnosu na metar,cm itd. Jel tako ili nije? Kad se može nešto kratiti a kad ne:Da li je ovo ispravno kraćenje? 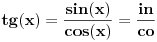 jer smo kratili s u brojniku i nazivniku,zatim lijeve male zagrade,x-ove i desne male zagrade. jer smo kratili s u brojniku i nazivniku,zatim lijeve male zagrade,x-ove i desne male zagrade.Ne valja tako kratiti jeli se slažete?(da ili ne?) Ajmo dalje. Da li se razlikuju geometrijski pojmovi luk i duž? Da li se dužina oba pojma mogu izraziti nekom jediničnom dužinom (SI ili proizvoljnom kako nam geometrija dozvoljava)? Da li je omjer (dužina luka/dužina radijusa) bezdimenionalan jer se istoimene jedinice krate iako se odnose na različite pojmove? Da li je dozvoljeno pokratiti istoimene jedinice i kad se odnose na različite pojmove.Naprimjer kad solimo kupus pa stavimo 3 kg soli na 150 kg kupusa.Lijepo to pokratimo pa imamo 0.02[ničega]? Možda je bolje reći 0.02[kg/kg] navodeći da je gore so,a dole kupus? 0.07 rad u SI sistemu je =0,07[metara(luka)/m(radijusa)] Da ili ne? [ holononi @ 18.06.2010. 06:36 ] @
Dužina je uvek dužina bez obzira šta se meri. Ali neki ovde izgleda ne razlikuju meru i merenu veličinu pa poistovećuju ugao i radijan. Nastava se ne može držati na takav način, definicije se ne mogu izmišljati zato što je to nekome tako došlo u trenutku nadahnuća već se moramo držati već dogovorenih definicija. Ako ne bi bilo tako onda je pitanje pogodnog trenutka da nekome dug od 500 dinara vratite sa 500 para jer je ste vi to tako definisali.
[ Sini82 @ 18.06.2010. 07:58 ] @
http://docs.google.com/viewer?...tbTgtM-VHTbPq3tUEZB80Jdr3knotg
Citat: Radijan je ugao u ravni između dva poluprečnika kruga koji na njegovom obimu isjecaju luk dužine jednake poluprečniku (1 rad=1 m/m=1). Ista kao i definicija u srednjim školama. Zašto je radijan m/m(=1) a ne kg/kg ili s/s ili A/A ili K/K ili mol/mol? Zato što je radijan mjera ugla u ravni. Zašto je steradijan m^2/m^2(=1)? Zato što je steradijan mjera ugla u prostoru. Radi se o dogovoru oko označavanja, ničemu drugom. Što i potvrđuje iz istog gore zakona: Citat: Dopunske jedinice SI smatraju se bezdimenzionalnim jedinicama SI. Što nas vraća na početak, sviđalo se vama ili ne, Nedeljko je u pravu. 1995. su radijan i steradijan uvršteni u izvedene jedinice SI, kada je kategorija dopunskih jedinica ukinuta; što ne mijenja suštinu stvari. [ Fitopatolog @ 18.06.2010. 08:11 ] @
Meni se sviđa kada je Nedeljko u pravu ali (nažalost) u ovoj temi nemam to zadovoljstvo...
[ holononi @ 18.06.2010. 08:30 ] @
U dokumemntu "Zakon o mernim jedinicama i merilima" stoji
Citat: Jedinica ugla u ravni je radijan. Radijan je ugao u ravni između dva poluprečnika kruga koji na njegovom obimu isecaju luk dužine jednake poluprečniku ( 1 rad = 1m/m = 1 ). Očigledno je da "pesnik" ne razlikuje merenu veličinu i jedinicu mere. U prvoj rečenici njemu je "jedinica ugla radijan" a u drugoj rečenici "radijan je ugao". Dakle dokument je kontradiktoran sam sebi. Osim toga ne kaže se "jedinica ugla" već "jedinica mere ugla". No, zakone u ovoj državi pišu (prepisuju) partijski poslušnici tako da na to ne bih obraćao previše pažnje. Samo bih još napomenuo da pored tih kardinalnih grešaka ima i tipografskih jer za steradijan treba da stoji m2m-2 = 1. [ Nedeljko @ 18.06.2010. 11:16 ] @
Citat: zzzz: Fizika i matematika nisu isto.SI sistem mjera vrijedi samo za dio fizke koji se zove tehnički dio a obavezno se koristi samo u javnoj upotrebi.To je propisano zakonom. OK, kako ćemo da izrazimo ugao pod kojim se vidi Sunce sa Zemlje? Citat: Sini82: Zašto je radijan m/m(=1) a ne kg/kg ili s/s ili A/A ili K/K ili mol/mol? Naravno da je sve to isto, kao što je 2/2=3/3. [ Cabo @ 18.06.2010. 14:59 ] @
Citat: Nedeljko: OK, kako ćemo da izrazimo ugao pod kojim se vidi Sunce sa Zemlje? Isto kao i svaki drugi ugao. U radijanima ili stepenima. Masa se izražava u kilogramima. Dužina se izražava u metrima (ili izvedenim jedinicama: mili-, centi-, deka-, itd.). Pritisak se izražava u paskalima. Itd. Nije ovo boks meč između matematike i fizike. [ Nedeljko @ 18.06.2010. 15:47 ] @
Citat: Cabo: Isto kao i svaki drugi ugao. U radijanima ili stepenima. Nije ovo boks meč između matematike i fizike. Naravno. [ galet@world @ 18.06.2010. 16:47 ] @
Pitanje je jednostavno a eskivaža matematičara je već po ko zna koji put očigledna.
Ako neki ugao podelimo sa uglom dobijemo broj bez dimenzije. Ako neki ugao podelimo brojem koji nema dimenziju dobijemo ugao. Dakle? [ holononi @ 18.06.2010. 17:22 ] @
Šta dakle? Deli se dužina sa dužinom. I tu nema vrdanja.
[ galet@world @ 18.06.2010. 17:33 ] @
A gde si zaturio ugao?
Ugao se meri uglom, a ne brojem bez dimenzije. Ugao je pojava koja se razlikuje od drugih pojava. ETO šta dakle. [ Fitopatolog @ 18.06.2010. 17:48 ] @
Nije ugao izuzetak npr. pojačanje (ili slabljenje) se meri u decibelima ili neperima...
[ galet@world @ 18.06.2010. 17:52 ] @
Odgovori na vrlo jednostavno pitanje:
Da li je radijan ugao ili nije? [ holononi @ 18.06.2010. 18:14 ] @
Neki uporno pokušavaju da budu papar za svaku čorbu. Ali topla voda i slični "izumi" su davno otkriveni. Najlepše je biti u centru sveta i sve se vrti oko tebe. Medjutim medjunariodni standardni i konvencije su utvrdjeni i prihvaćeni. Zato turanje glave u pesak liči na navlačenje ludačke košulje na sopstvenu glavu. Svakako da smo mogli da crvenu boju nazovemo zelenom "jer je ima na drveću". Isto tako i sa radijanom, definisan je tako kako je definisan. Naša obaveza je da prenosimo tu definiciju takva kakva je bez obzira da li nam se dopada ili ne. Postoje i procedure za promenu te definicije. Uostalom, setite se samo da je do skora metar bio četrdesetmilioniti deo zemljinog obima a danas se definiše predjenim putem svetlosti.
Ko zna možda će baš protivnici aktuelne definicije radijana jednog dana likovati i gledati nas s visina "a šta sam ti rekao" i zati sledi macola naravno. Osnivanje kluba ili pokreta za promenu definicije radijana bi mogao biti prvi korak. A ovde se naziru centri kristalizacije. [ japan @ 18.06.2010. 18:21 ] @
Citat: galet@world: Odgovori na vrlo jednostavno pitanje: Da li je radijan ugao ili nije? Ako se meri u pravcu kazaljke na satu, onda jeste, u suprotnom nije. A ako se posmatra sa zadnje strane sata, onda je jeste samo ako je sat digitalni. [ galet@world @ 18.06.2010. 18:45 ] @
Neki uporno pokazuju da ne znaju o čemu se radi. Niko ne dovodi u pitanje definiciju radijana.
Oni jednostavno ne shvataju šta je definisano. Tom definicijom određena je ili definisana je VELIČINA mernog ugla A što tiče se papra, čorbe i tople vode to su jednostavno elementi nepristojne eskivaže i, naravno, nisu odgovor na postavljeno pitanje. [ holononi @ 18.06.2010. 18:58 ] @
SI definiše jedinice mere a ne veličine.
[ galet@world @ 18.06.2010. 19:49 ] @
Citat: holononi: SI definiše jedinice mere a ne veličine. To nije tačno jer se mora definisati i veličina jedinica mere. ili koliki deo neke pojave uzimamo kao njenu mernu jedinicu [ holononi @ 18.06.2010. 21:01 ] @
Spolja ili iznutra?
[ Cabo @ 18.06.2010. 21:04 ] @
Galet, ne paziš na času.
Ne definiše se veličina, već jedinica mere, preko veličine. /facepalm [ galet@world @ 18.06.2010. 21:35 ] @
Citat: Cabo: Galet, ne paziš na času. Ti možda paziš, ali ne razumeš. Jedina bitna stvar kod definicije merne jedinice i jeste njena veličina jer se pri tom drugo ništa i ne definiše - merna jedinica nije definicija pojave - ona je njen deo. Dakle - je li radijan ugao ili nije? Zašto izbegavate direktan odgovor na ovo pitanje? Citat: holononi: Spolja ili iznutra? In medias res. [ holononi @ 19.06.2010. 07:36 ] @
Predlažem da se ova tema podeli u dva dela. Prvi deo treba da ostane u forumu matematika jer tu ima dosta korisnih saveta za one koji se uče. Drugi deo, od momenta kad su pojedini "izumitelji tople vode" počeli po svaku cenu da se uvlače u ludačku košulju, premestiti u temu "kako mali djokica zamišlja svemir" ili nešto tako.
[ galet@world @ 19.06.2010. 15:16 ] @
Citat: holononi: Predlažem da se ova tema podeli u dva dela. Prvi deo treba da ostane u forumu matematika jer tu ima dosta korisnih saveta za one koji se uče. To je u redu jer ima nešto da naučiš što nisi znao. Citat: Drugi deo, od momenta kad su pojedini "izumitelji tople vode" počeli po svaku cenu da se uvlače u ludačku košulju, premestiti u temu "kako mali djokica zamišlja svemir" ili nešto tako. Autoru ovog teksta jasno je kako treba da se zamišlja svemir za razliku od "malog đokice" pa bi dobro bilo da nam to pokaže. [ boxxter @ 19.06.2010. 17:32 ] @
Citat: holononi: Predlažem da se ova tema podeli u dva dela. Prvi deo treba da ostane u forumu matematika jer tu ima dosta korisnih saveta za one koji se uče. Drugi deo, od momenta kad su pojedini "izumitelji tople vode" počeli po svaku cenu da se uvlače u ludačku košulju, premestiti u temu "kako mali djokica zamišlja svemir" ili nešto tako. Znam ja kako mali djokica zamislja svemir - " Ako zamislimo dva voza koji putuju brzinom svetlosti...". Eto tako. To uopste nije za ludacku kosulju xD. To je sasvim normalno. =) Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|