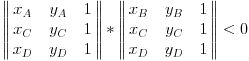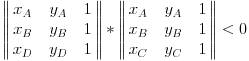[ Divjak @ 05.01.2005. 17:13 ] @
| Pisem program za proveravanje maximalnog broja preseka duzi u koordinatnom sistemu... Medjutim nikako mi ne pada na pamet kako da proverim da li se dve duzi seku ako imam njihove x1,y1,x2,y2 koordinate.... a da ne proveravam da li imaju zajednicku tacku, jer mi to nije dovoljno precizno... Unapred hvala... |