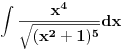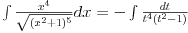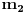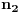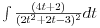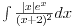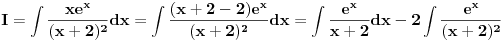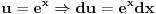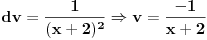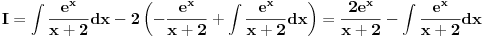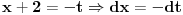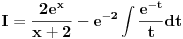[ Miloš Bjelanović @ 18.01.2005. 20:21 ] @
|
[ cicika @ 18.01.2005. 21:32 ] @
To je tzv. integral binomnog diferencijala.
Integral oblika: 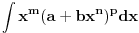 gde su: gde su: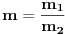 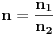 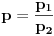 rešava se jednom od sledećih smena: 1. 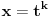 gde je gde je 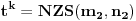 pod uslovom da je pod uslovom da je  ceo broj. ceo broj.2. 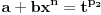 ako je ako je 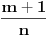 ceo broj ceo broj3. 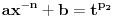 ako je ako je 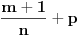 ceo broj. ceo broj.Dakle predstaviš dati integral u obliku: 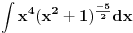 pogledaš data pravila i voziš pogledaš data pravila i voziš P.S. Ima nekih problema sa prikazivanjem tex-a, ako se neke stvari ne vide refreshuj stranu dok se ne pojave. Moguće je i da mene malo zeza konekcija [ Miloš Bjelanović @ 19.01.2005. 06:06 ] @
[ cicika @ 19.01.2005. 11:48 ] @
Vrlo jednostavno:
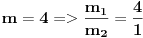 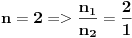 Slučaj u datom integralu je sledeći:  nije ceo broj. Takodje, nije ceo broj. Takodje, 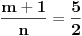 nije ceo broj, ali nije ceo broj, ali 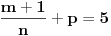 jeste ceo broj pa ti je potrebna smena pod brojem 3 iz mog prethodnog posta. jeste ceo broj pa ti je potrebna smena pod brojem 3 iz mog prethodnog posta.Kad uvedeš smenu biće ti potrebno znanje integrisanja racionalnih f-ja kao i neke rekurentne formule u vezi sa tim. Što se tiče ovog drugog integrala koji si postavio treba da uočiš sledeće: 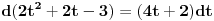 Onda uvedeš smenu (koja zapravo i nije potrebna ali ako ti je tako lakše i preglednije onda OK) 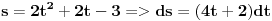 čime se dati integral svodi na čime se dati integral svodi na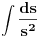 što je tablični integral. što je tablični integral.Ako smem da pitam za šta ti trebaju ovi integrali, tj. koja škola/fax i tako to? [ Miloš Bjelanović @ 19.01.2005. 12:30 ] @
Zar nisi primjetila da sam već uradio binomni diferencijal?
Dakle, kad sam uradio smjene i sve sveo na  sad opet liči na binomni, i opet sam radio binomni i na kraju se vratim na onaj integral koji sam dobio poslije uvođenja smjene sad opet liči na binomni, i opet sam radio binomni i na kraju se vratim na onaj integral koji sam dobio poslije uvođenja smjene 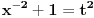 , tj. , tj. 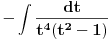 . .Mene zanima šta da radim s ovim 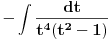 . .Citat: Ako smem da pitam za šta ti trebaju ovi integrali, tj. koja škola/fax i tako to? Spremam ispit iz matematike 1 za Saobraćajni fakultet. [ cicika @ 19.01.2005. 13:22 ] @
Nisam primetila jer ga nisam radila a i opet me prikaz tex-a zeza.
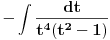 rastavljaš na tri racionalne f-je u čijim imeniocima će se naći samo rastavljaš na tri racionalne f-je u čijim imeniocima će se naći samo 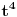 odnosno odnosno 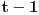 i i 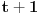 . .Trenutno nemam vremena da kuckam to, ali iskucaću večeras. Prijateljski savet - vrati se na integrale racionalnih funkcija, pogledaj pravila za rastavljanje na zbir racionalnih f-ja u čijim imeniocima su faktori polazne f-je. Teško je raditi komplikovanije stvari ako se ne znaju neke osnovne. I nemoj da se ljutiš što ti to kažem, ja sam na ETFu, položila sam četiri matematike + verovatnoću i statistiku, prosto znam kako to ide. Inače, integracija racionalnih f-ja ima jako široku primenu jer se masa drugih integrala (prvenstveno integrali iracionalnih, trigonometrijskih f-ja) uvodjenjem smena svode na integrale racionalnih f-ja, koji su u suštini jako dosadni jer se svode na često vrlo dugačka izračunavanja (kako bi jedan od mojih profesora na faksu rekao "Prisustvo tela, odsustvo duha"). Kod recimo integrala iracioalnih f-ja postoji nekoliko vrsta smena i sve se svodi na to da prepoznaš koju treba da primeniš a pravila za njihovu primenu su jako stroga tj. odredjena pa je teško pogrešiti. Isto važi i za integrale trigonometrijskih f-ja mada za njih ponekad treba i malo "kreativnosti", ponekad treba primeniti neku od trigonometrijskih transformacija. Matematika prosto mora da se uči nekim redom. Pozdrav, Tijana [ Miloš Bjelanović @ 28.01.2005. 19:27 ] @
[ lampica @ 29.01.2005. 14:27 ] @
Citat: Miloš Bjelanović Kako se radi ovaj sa apsolutnom vrijednošću??? Bilo koji zadatak sa apsolutnom vrednošću (pa i integral) se radi primenom definicije apsolutne vrednosti koja ti daje dva slučaja, a onda je to manje "strašan" zadatak. Znači, 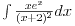 ako je x nenegativan broj (veći od nule, ovde otpada mogućnost da je jednak nuli) 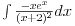 ako je x negativan broj... [ zoranpr @ 29.01.2005. 16:47 ] @
Zasto ne odes kod asistentkinje Tijane i pitas sve sto ti nije jasno. Ona je super i uvek hoce da pomogne. Ne znam da bilo ko ima negativno misljenje, iskustvo sa njom.
[ darkosos @ 01.02.2005. 19:56 ] @
Ne garantujem, ali postoje ozbiljne indicije da se tražena primitivna funkcija ne može izraziti konačnom kombinacijom elementarnih funkcija.
Obrtao sam ga i okretao, ali izgleda da se svodi na integral funkcije 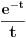 što je tzv. eksponencijalni integral: http://mathworld.wolfram.com/ExponentialIntegral.html što je tzv. eksponencijalni integral: http://mathworld.wolfram.com/ExponentialIntegral.htmlUostalom, i MathCad daje takvo rešenje. Ako bi dole bilo (x+1)2, nešto bi se skratilo i mogao bi jednostavno da se reši. [ cicika @ 01.02.2005. 21:29 ] @
A dalje ima sve varijante. Prva je da razvije
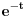 u Tejlorov red (što spada u Advanced zadatke na tom kursu matematike koji on polaže) ili da primeni kompleksnu integraciju (koja uopšte ne spada u taj kurs matematike). Jedino što je to bio neodredjen integral pa ne znam baš kako bi primenili kompleksu integraciju. u Tejlorov red (što spada u Advanced zadatke na tom kursu matematike koji on polaže) ili da primeni kompleksnu integraciju (koja uopšte ne spada u taj kurs matematike). Jedino što je to bio neodredjen integral pa ne znam baš kako bi primenili kompleksu integraciju.[ darkosos @ 02.02.2005. 09:42 ] @
[ Lalemajstormoler @ 14.04.2005. 21:45 ] @
Svaka vam cast
pa vi treba da ucite sto godina da bi ovo naucili ako prethodno ne prolupate. Sto se nadam da necete. Poz.....Lale [ KPYU @ 15.04.2005. 01:41 ] @
Naprotiv, dovoljno je par meseci (2-3), ako ne želiš da zaboravljaš. Ako želiš da zaboravljaš, opet super. Svakih nedelju dana krećeš iz početka.
Verovali ili ne, teže je naučiti rad na računaru, gde ti se neće baš sve svesti na prepoznavanje šablona, kao što ovde, u integralima, hoće. [ Djina 94. @ 22.09.2009. 14:20 ] @
Kako da uradim ovaj zadatak
x ∫y<=>x+y=0 [ Nedeljko @ 22.09.2009. 16:08 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|