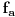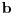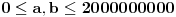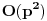[ kajla @ 02.05.2002. 13:58 ] @
| 1. Fabonačijev niz brojeva formira se po sledećem zakonu: F1=1, F2=1; Fn=Fn-1+Fn-2, za n>=3 Odrediti poslednju cifru 1996. člana Fabonačijevog niza. 2. Naći 7 prostih brojeva koji su manji od 1000 i koji čine aritmetički niz. (aritmetički niz je niz u kome je razlika svaka dva susedna člana konstantna) poz. |