Pa bas niko nema da mi ukaze barem na neki link ?

Mozda mislis na faktorijal, (na nemackom se kaze fakultet).

na primer
5! = 1 * 2 * 3 * 4 * 5, tj
n! = 1*2*...*n

s tim da je 0! = 1...

ako si na to mislio :).

Da na to sam mislio :) a ima li nekih osnovnih primjera za pocetnike ?

i Hvala puno na pomoci...

Pa nema bas. Tipa ne mozes da saberes dva faktorijala i sl. (tj mozes ali ne postoji nista spec oko toga m!+n! ostaje m!+n!). E sad od stvari koje jos treba znati tu su:

(2k)!! i (2k+1)!! odnosno mnozenje samo parnih odnosno neparnih brojeva, pri cemu vazi
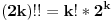
tu je i


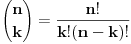
Iz same definicije je ocigledno da je faktorijal rekurzivna f-ja odnosno vazi:

n!=n*(n-1)!

a tu je i gama f-ja:


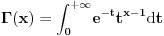
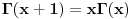
koju pominjem zato sto va nju vazi , odnosno za celobrojne x:

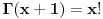
Ne pada mi nista vise na pamet.

Počelo je to od permutacija.Na koliko se različitih načina može poredati
N elemeneta?
AB ,BA-2 načina.ABC,ACB,BAC,BCA,CAB,CBA-6 načina.
4 elementa moguse poredati na 4*3*2*1 način.N elemenata ide na
n!=n*(n-1)*(n-2)*....*3*2*1 način.Onda se to primijenilo u kombinatorici
i za složenije stvari.Poslije i za još neke teške matematike.
Čak je uvedeno i 0!=1 kao neki dogovor jer se onda lako mogu napisati
neke formule koje bi bile dugačke ko domaće sremske kobasice.

Nije loše znati kako se do formule dolazi, prilično je jednostavno, a može pomoći intuiciji:

1. Neka je P(n) broj rasporeda n elemenata (čiju formulu za sada ne znamo). Zamislimo da su dati elementi raspoređeni na neki način. Gde možemo umetnuti još jedan element? Između bilo koja dva već poređana, na početku ili na kraju. Lako se vidi da takvih mesta ima n+1, pa je prema tome P(n+1) = (n+1) * P(n). Odmotavajući ovo do 1 (ili do 0) dobijamo datu formulu.

2. Zamislimo da imamo n predmeta i n mesta (npr. kutija) u koje ih možemo staviti. Pri postavljanju prvog predmeta, imamo n mogućnosti. Kada njega postavimo, ostalo je još n-1 mesto za drugi. Itd., n-2 za treći, dok ne ostane jedan predmet i jedno mesto.