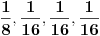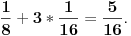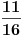A jel treba određen broj poena da se dostigne ili se igra određen broj igara?

B dobija samo kad pobedi tri partije, a izgubi najviše jednu, tj BBB, BBAB, BABB, ABBB.
Verovatnoće su redom:
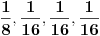
Ukupno
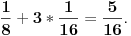
Vidimo da šansa da izgubi iznosi
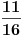
Dakle dobit treba podeliti u odnosu 11:5

Može se razmatrati opštji problem: prvom treba i pobeda, a drugom j. Dakle, preostaje slučaj kada je i>j. Ako označimo verovatnoću pobede prvog sa v(i,j), onda za sve prirodne brojeve i,j važi:
v(1,j)=1-q^j
v(i,1)=p^i
v(i,j)=p*v(i-1,j)+q*v(i,j-1), za i,j>1,
gde je p verovatnoća pobede prvog, a q drugog igrača u jednoj partiji. U našem slučaju je p=q=1/2, pa se račun može pojednostaviti korišćenjem jednakosti v(j,i)=v(i,j) i v(i,i)=1/2. U svakom slučaju, dobija se da je verovatnoća da prvi pobedi jednaka p*1/2+q*p^3=5/16. Ovo je zadatak koji se uzima kao zadatak sa kojim je nastala teorija verovatnoće.

Mislio sam da ce biti malo teze (dosta je lako krenuti krivim razmisljanjem - prvi nedjeljkov post)... Pozdrav :)

A šta fali mom prvom postu?

Pa fali mu verovatno to što ga dečko nije razumeo :) Mada razumem, dao nam je 2 tjedna (sumljajući), a vi ga odma' pocepaste, k'o besan pas masno ćebe. I tako ste mu upropastili zadovoljstvo da posle ta dva tjedna trijumfalno nam objavi svoje čudesno rešenje. Nije računao na to da ovde ima profi likova.

Polako Darko.Mario je zadao taj zadatak,a onda su KPYU i Nedeljko to nekako
uspjeli riješiti.Ali!Odi ti u kladionicu pa upitaj:Koliko para ću dobiti ako se kladim
na onog 5/16,ako uložim 5 dinarića.Kažu vam lijepo "X".Onda upitaš:A koliko
ako uložim na onog 11/16 svojih 11 din.Opet vam kažu "Y":Ako kladionica
radi sa dobiti od 20%,koliki su oni X i Y?

Pa baš i nisu "nekako". Jer, za profesionalce, to je azbuka verovatnoće. Kao što Nedeljko reče, ovaj zadatak ima istorijski značaj i pominje se u uvodu kursa verovatnoće.

Što se tiče tvog zadatka nemam pojma. Ne znam ni šta znači to da kladionica radi sa 20% dobiti? U stvari ne znam ni kako funkcioniše kladionica niti sam ikad bio u nekoj. A ne volim nešto ni tu verovatnoću, kad smo već kod toga. Ako 'oćeš na 'ladno pivo, može ;)

Ajde kad si navalio. Ako na onog slabijeg uložiš 5 dinara daće ti 5/(5/16)*(1-20%)=12.8 dinarčića u slučaju da on pobedi. Isto će ti dati 11/(11/16)*(1-20%)=12.8 dinarčića ako uložiš na jačeg i on pobedi.

Ako uložiš X dinarčića na igrača čije su procenjene šanse za pobedu jednake p, a kladionica posluje sa dobiti od d%, onda dobijaš X/p*(1-d/100) dinarčića ako on pobedi.

U našem slučaju, ako uložiš 5 dinarčića na slabijeg i 11 na jačeg, dobićeš 12.8 dinarčića bez obzira na ishod meča. Drugim rečima, sigurno gubiš tačno 20% od uloga.

Samo da čestitam nedeljku na rješenju.Mogao bi voditi neku kladionicu
umjesto što ovdje uludo ubija dosadu.A za pivo jesam.Čim malo
prođe ovaj sibirski val.