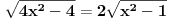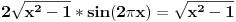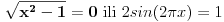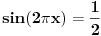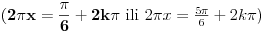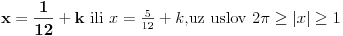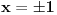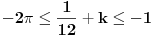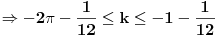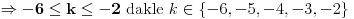[ nemanjaa @ 02.02.2005. 23:36 ] @
| evo jedan zadatak sa proslogodisnjeg fonovog prijemnog... treba odrediti koliko resenja imam jednacina ( u resenju mi pise da ima 6 ali mene zanima postupak.. kako doci do tih 6 resenja) sqrt(4x^2-4)* sin2pix= sqrt(x^2-1) koja zadovoljavaju uslov |x|<=2pi hvala |