Ne moze.

Pretpostavimo da moze, neka je povrsina trougla P i duzina stranice a.

Lako je dokazati sledece dve stvari:

1) ako imamo duz duzine d ciji su krajevi celobrojne koordinate, tada je d² celobrojno
2) dvostruka povrsina trougla ciji su krajevi celobrojne koordinate je celobrojna

Kako je 2P = a² * sqrt(3), to je kontradikcija da su 2P i 2² oba celobrojni.

Za ostale pravilne mnogouglove...

Baš šteta, bilo bi lepo da može. Thnx

'Teo sam nešto da kažem pametno, ali mi se izjalovio plan :)

Kako god, imao sam ideju sledećeg tipa. Ti pravilni mnogouglovi su invarijantni, da tako kažem, na rotacije za celobrojni umnožak njihovog centralnog ugla, oko centra opisanog/upisanog kruga. Mreža, s' druge strane, je invarijantna samo na rotacije za celobrojni umnožak pravog ugla, dok za centar imamo nekoliko uopštenih kandidata, sad me mrzi da nabrajam i razmišljam da li sam nešto ispustio.

Šta htedoh reći? Ovo bi moglo da bude dobrano ograničenje za mogućnost konstruisanja pravilnog mnogougla, sem kvadrata.

Eto tol'ko, ako neko želi da razradi...

Tvoje je pitanje ekvivalentno sa pitanujem da li se može konstruisati takav poligon u racionalnoj mreži. Nadovezao bih se na gpredu. Tvrđenje 2) je potpuno tačno, ali ga je potrebno obrazložiti. Oba tvrđenja 1) i 2) takođe važe i kada se u formulaciji celi brojevi zamene racionalnim.

Najpre primetimo da tvrđenje 2) važi u slučaju kada trougao ima dve ivice paralelne koordinatnim osama Neka je dat proizvoljan trougao ABC u celobrojnoj (racionalnoj) mreži i neka je PQRS najmanji pravougaonik u kome je sadržan trougao ABC, a koji ima ivice paralelne koordinatnim osama. Tada će njegova temena takođe biti u celobrojnoj (racionalnoj) mreži, a površina trougla ABC jednaka razlici površine pravougaonika PRQS i površina najviše tri trougla čija su temena u celobrojnoj (racionalmnoj mreži).

Što se tiče pravilnog poligona sa n temena, ako su njegova temena u racionalnoj rešetki, jednačine simetrala stranica će imati racionalne koeficijente, pa će i njihov presek (centar opisanog kruga) biti u racionalnoj rešetki, odakle će i kvadrat poluprečnika R opisanog kruga biti racionalan broj. Površina bilo kog od trouglova čija su temena centar opisanog kruga i dva susedna temena pravilnog poligona jednaka je

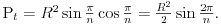
Prema prethodnom, površina tog trougla mora biti racionalan broj, odakle i navedeni sinus mora biti racionalan broj, pa kvadarat kosinusa istog ugla mora takođe biti racionalan broj. Označimo sinus tog ugla sa s, a kosinus sa c. Tada za broj a=c+is, gde je im imaginarna jedinica mora da važi

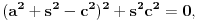
to jest, broj a mora biti rešenje jednačine četvrtog stepena sa racionalnim koeficijentima. Broj 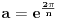je rešenje jednačine zⁿ-1=0. Međutim, broj 1 je takođe rešenje te jednačine, a pošto je za n>1 broj a različit od 1, onda je on i rešenje jednačine
z^n-1+...+z+1=0
koja se dobija delenjem pretodne jednačine sa z-1. Pretpostavimo sada da je n=p prost broj. Polinom P(z)=z^p-1+...+z+1 je nerastavljiv na proizvod dva polinoma sa celim koeficijentima stepena bar jedan zato što je takav i polinom

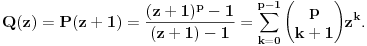
Zaista, ako bi polinom Q(z) bio rastavljiv na proizvod polinoma 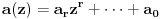i 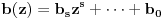, sa celim koeficijentima onda njihovi vodeći koeficijenti ne bi bili deljivi sa p budući da je p prost broj, a vodeći koeficijent polinoma Q(z) nije deljiv sa p. Međutim, onda bi postojali najmanji celi nenegativni brojevi i,j takvi da 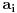i 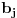nisu deljivi sa p. Ali, onda ni koeficijent uz 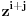u polinomu Q(z) ne bi mogao da bude deljiv sa p. Jedini takav koeficijent u polinomu Q(z) je vodeći, što znači da su svi koeficijenti polinoma a(z) i b(z) osim vodećih deljivi sa p, pa pošto se radi o polinomima stepena barem jedan, njihovi slobodni članovi moraju biti deljivi sa p. Ali onda bi slobodni član polinoma Q(z) koji je jednak p morao da bude deljiv sa p², što je kontradikcija. Ovo je takozvani Ajzenštajnov kriterijum za nesvodljivost polinoma prepričan u ovom našem posebnom slučaju.

Po Gausovoj lemi je polinom Q(z) (a samim tim i P(z)) nerastavljiv i na proizvod dva polinoma sa racionalnim koeficijentima stepena bar jedan. Da bi se to dokazalo, uvedimo najpre pojam primitivnog polinoma. To je polinom sa celim koeficijentima koji ima osobinu da niti jedan prost broj nedeli sve njegove koeficijente, odnosno da su njegovi koeficijenti u ukupnosti uzajamno prosti. Najpre se sličnom metodologijomm kao malopre dokazuje da je proizvod dva primitivna polinoma primitivan. Zatim se pretpostavi da je polinom P(z) sa celim koeficijentiima rastavljiv na proizvod dva polinoma sa racionalnim koeficijentima stepena bar jedan. Tada bismo ga najpre napisali kao proizvod ta dva polinoma sa racionalnim koeficijentima u neskratljivom obliku, potom izvucimo ispred svakog od njih NZS (recimo, pozitivne vrednosti) imenilaca svih njegovih koeficijenata različitih od nule. Označimo te NZS sa 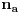i 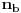. Dobićemo polinom P(z) u obliku proizvoda dva polinoma a'(z) i b'(z) sa celim koeficijentima podeljen sa dva prirodna broja. Može se desiti da ispred polinomi a'(z) i b'(z) nisu primitivni. Izvucimo ispred njih NZS (recimo pozitivne vrednosti) njihovih koeficijenata i označimo ih sa 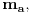odnosno 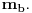Tako ćemo dobiti polinom P(z) u obliku proizvoda dva primitivna polinoma a''(z) i b''(z) i dva prirodna broja, podeljen sa proizvodom dva prirodna broja. U svakom slučaju, proizvod q ta dva razlomka mora biti ceo broj da bi ceo proizvod bio celobrojan polinom, budući da je proizvod dva primitivna polinoma primitivan. Ali, onda važi P(z)=(q*a''(z))*b''(z), Međutim, tada je polinom P(z) predstavljiv ka proizvod dva polinoma sa celim koeficijentima stepena barem jedan.

Međutim, naš polinom P(z) sa celim koeficijentima nije rastavljiv na proizvod dva polinoma sa celim koeficijentima stepena barem jedan, pa prema prethodnom ni na proizvod dva polinoma sa racionalnim koeficijentima stepena barem jedan. Ali pošto je broj a koren polinoma P(z), iz njegove nerastavljivosti sledi da nije koren niti jednog polinoma sa celim (racionalnim) koeficijentima nižeg stepena (ako isključimo konstantan nula polinom). U suprotnom bi on bio i koren njihovog NZD, koji bi kao delitelj nerastavljivog polinoma P(z) bio konstantan nenula polinom, koji nema niti jedan koren, pa ni a, što daje kontradikciju.

Iz ovoga i zaključka sa početka da bi u slučaju postojanja pravilnog poligona sa n temena u racionalnoj mreži morao da postoji polinom četvrtog stepena čiji je a koren sledi da ne postoji pravilan poligon sa n temena u racionalnoj mreži kada je n prost broj veći od 5. Ako je n=5, onda je broj a=c+is koren polinoma z^4+z^3+z^2+z+1. Pošto je c^2+s^2=1, biće 1/a=c-is, pa ako jednačinu z^4+z^3+z^2+z+1=0 podelimo sa z^2 dobijamo da za t=a+1/a=2c važi t^2+t-4=0, odakle zbog c>0 (jer je 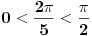) važi 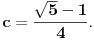Odatle je i 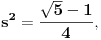pa pošto to nije racionalan broj (a još manje kvadrat racionalnog broja), pravilan petougao ne postoji u racionalnoj mreži.

Pravilan trougao ne postoji u racionalnoj mreži zato što je 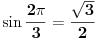iracionalan broj. Sa druge strane, ako je m>2 delitelj broja n i pravilan n-tougao postoji u racionalnoj mreži, onda bismo odabiranjem svakog k-tog temena tog pravilnog n-tougla za k=n/m dobili pravilan m-tougao u racionalnoj mreži. Na taj način možemo zaključiti da ako postoji da ako postoji pravilan n-tougao u racionalnoj mreži, da n mora biti potpun stepen dvojke. Ali, u racionalnoj mreži ne postoji pravilan osmougao jer je 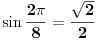iracionalan broj, pa u slučaju postojanja pravilnog n-tougla u racionalnoj mreži mora biti n=4. Pravilan četvorougao u racionalnoj mreži postoji, a prema prethodnom pravilan n-tougao ne može postojati niti za jedno n različito od 4, čime je problem u potpunosti rešen.

Inače, polinom P(z) se zove polinom deobe kruga na n jednakih delova, ali samo u slučaju kada je n=p prost broj. U opštem slučaju se polinom 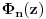deobe kruga na n jednakih delova izračunava po rekurentnoj formuli

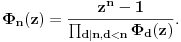
Pritom svi ti polinomi imaju cele koeficijente u skupu {0,1,-1}, nerastavljivi su na proizvod dva polinoma sa celim (racionalnim) koeficijentima stepena bar jedan, i koreni polinoma 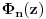su tačno brojevi oblika 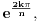gde je k prirodan broj uzajamno prost sa n. Svaki koren im je ybog nerastavljivosti jednostruk, a stepen polinoma deobe kruga na n delova je 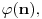gde je 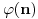Ojlerova funkcija - broj uzajamno prostih prirodnih brojeva sa prirodnim brojem n, ali koji nisu veći od n. Ta funkcija je multiplikativna, to jest za uzajamno proste prirodne brojeve m i n važi [tex[\varphi(mn)=\varphi(m)\varphi(n).[/tex] Ona se može izračunavati i po formuli

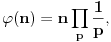
gde se množenje vrši po svim prostim deliteljima broja n, pri čemu se svaki uzima tačno jedanput. Ako je a prirodan broj uzajamno prost sa n, onda je po Ojlerovoj teoremi broj 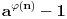deljiv sa n. Na ovoj formuli i multiplikativnosti Ojlerove funkcije funkcioniše RSA algoritam za kriptovanje javnim ključem. Specijalan slučaj Ojlerove teoreme kada je n=p prost broj se zove mala Fermaova teorema. Polinomi deobe kruga potiču od Gausa i njegvih ispitivanja konsruktibilnosti pravilnih poligona lenjirom i šestarom. On je dao potreban i doboljan uslov po n da pravilan n-tougao bude konstruktibilan lenjirom i šestarom i tom prilikom otkrio konstrukciju pravilnog 17-tougla lenjirom i šestarom koja je uklesana na njegovom nadgrobnom spomeniku.

<sub>[Ovu poruku je menjao Nedeljko dana 11.02.2005. u 00:25 GMT+1]

[Ovu poruku je menjao Nedeljko dana 11.02.2005. u 00:30 GMT+1]</sub>

Mogao si Nedeljko to i kraće napisati.Zaboli me glava čitajući
ovo.Ali eto slažem se,a šta ću.

Ja verujem. Zanimljivije mi je bilo dok sam lupao glavu da skontam dokaz tvrđenja 2 od gpreda... (uspeo sam, heh ;-))

Nisam mogao kraće, jer su zaista neophodna dublja razmatranja za ovu problematiku. Ne mogu se izbeći polinomi deobe kruga, a koristio sam ih minimalno. Sve sam uprostio koliko je moguće.

Inače, Darkova ideja ne može tek tako da prođe jer se kvadrat sa temenima A(0,0), B(5,0), C(5,5), D(0,5) može zarotirati za ugao arctg(0.75) u pozitivnom smeru, i tako će se dobiti kvadrat sa temenima A'(3,0), B'(7,3), C'(4,7), D'(0,4).

Ne vredi, uvek moram da se izblamiram. Jedna ispravka. Ojlerova funkcija se može računati po formuli

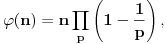
pri čemu se množenje vrši po svim prostim brojevima p koji dele n uzimakući svaki od njih po tačno jedanput.

Wow, mislim da je N.S. potukao sve rekorde u dužini post-a na ovom forumu. Mislim, svaka čast, ja ne bih imao živaca, čak i da znam sve to.

@Nedeljko
Imao sam identičnu ideju za dokaz 2). Jel' to nešto standardno, ili se poklopilo?

Oko koje tačke si rotirao taj kvadrat? Da li je to tačka u mreži?
'Ajde da je recimo dogovor da kada kažemo "tačka mreže" mislimo samo na tačke koje su presek dve ortogonalne prave u mreži.

Ja sam prvenstveno mislio na rotacije oko centra opisanog ili upisanog kruga u pravilni mnogougao. Jasno je da ta tačka mora ili biti tačka mreže ili tačka koja predstavlja centar nekog kvadrata mreže, jer samo tako može biti podjednako udaljena od svih tačaka poligona, koje su sve tačke mreže. Dakle mislim na rotacije koje ne menjaju položaj poligona.

Sto se tice leme koja je stavljena pod 2), ona vazi za bilo koji poligon cija su temena celobrojne koordinate. Dvostruka povrsina tog poligona je (dosta elegantna formula):

2P = 0;
for (i = 0; i < n; i++)
2P = 2P + (x_i - x_i+1) * (y_i + y_i+1);
(naravno x_n = x₀ i y_n=y₀)

Formula se 'vidi sa slike', samo treba nacrtati odgovarajuce trapeze [(x_i, 0), (x_i+1, 0), (x_i+1, y_i+1), (x_i, y_i)].

Zasto centar kruga mora biti 'tacka mreze' ili centar neke tacke mreze?

@darkosos

Kada sa stigao do racionalnosti sinusa, ostalo bi trebalo da je standardno sa kurseva algebre. Mislim da su to stvari koje bi morale da se rade iz algebre, (stepen algebarskog elementa, minimalni polinom, Gausova lema, Ajzenštajnov kriterijum, polinomi deobe kruga i njihove osobine, raširenja polja koja sam ovde izbegao sa njihovim osobinama,) ali koje se na žalost često ne rade. Ja recimo nisam učio nigde na studijama polinome deobe kruga.

Možeš da rotiraš kvadrat sa temenima A(-5,-5), B(5,-5), C(5,5), D(-5,5) oko koordinatnog početka O(0,0) koji je ujedno i centar kvadrata ABCD za isti ugao arctg(0.75) i dobićeš kvadrat sa temenima A'(-1,-7), B'(7,-1), C'(1,7), D'(-7,1). Da, kada je poligon invarijantan, onda budući da poteoremi koju sam dokazao poligon mora biti kvadrat, rotacije moraju biti za umnožak pravog ugla, pa tvoje tvrđenje važi. Međutim, to treba dokazati, a tvoja ideja mislim da ne vodi rešenju jer je problem tesno povezan sa stepenom sinusa spoljnog ugla pravilnog n-tougla u odnosu na određeno polje (ovde je to Q), a problem se može ranopravno razmatrati i opštije, u rešatkama nad drugim poljima. Sa prmerom sam hteo da istaknem važnost netrivijalnih položaja poligona, a samim tim i njihovih netrivijalnih rotacija.

Sa tom idejom si mogao još da pokažeš da i kosinus istog ugla mora biti racionalan broj, čime bi se izbeglo posebno razmatranje pravilnog petougla snižavanjem stepena broja 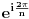sa 4 na 2, ali to je u principu sve. Naime, već sam pomenuo da centar poligona mora biti racionalan broj, pa se može pretpostaviti da je reč o koordinatnom početku. Ako je c kosinus, a s sinus spoljnog ugla tog poligona, a A(x,y) jedno od njegovih temena, onda će jedno od temena biti i A'(cx-sy,sx+cy). Međutim, teme pravilnog poligona ne može biti istovremeno i njegov centar, pa je barem jedan od brojeva x,y različit od nule. Ali, tada se korišćenjem činjenica da su x i y racionalni brojevi, kao i da je s racionalan broj zaključuje da je i broj c racionalan. No, tada je broj a=c+is, gde je i imaginarna jedinica, rešenje jednačine 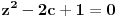sa racionalnim koeficijentima.

Ostatak zahteva dublja razmatranja. Kada bi ti našao jednostavno rešenje problema, ti bi dokazao da stepen broja 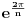za n>2 može biti manji od 3 samo za n=4, a to je već u direktnoj vezi sa faktorizacijom polinoma deobe kruga, to jest njegovom nerastavljivošću, što sudeći po istoriji matematike i naporima velikih matematičara da dokažu tu teoremu u opštem slučaju nije jednostavan zadatak. Dokaz te teoreme možeš naći u knjizi Algebra II od Veselina Perića. Ipak, ovde je dovoljno znati kada taj stepen nije veći od dva, što je slabije od tačnog utvrđivanja stepena, ali ne vidim kako bi se to iskoristilo.

Nisam ja sad tu skontao tu bitnoću rotacije, a naravno ni Nedeljkov dokaz. Nemojte me kriviti, volim dokaze koji ne zahtevaju poznavanje brda teorije. Ali sam video da je tvrđenje 2 korektno, kao što se da videti na slici.

Na slici je prikazan konstruktivni postupak računanja površine proizvoljnog trougla u kvadratnoj mreži, koji se dobija kao sabiranjem i oduzimanjem površina 6 pravouglih trouglova.

Ovaj postupak je takođe prenosiv i na racionalnu mrežu.

Tvrđenje takođe važi za proizvoljan poligon u mreži jer se svaki poligon može podeliti na trouglove.

@Nedeljko

Ne znam šta si navalio na racionalne brojeve. Ovo bi moglo da bude (ne kažem jeste) mnogo jednostavnije. Racionalni brojevi imaju jednu "neugodnu" karakteristiku, o kojoj celi mogu samo da sanjaju, a to je da između svaka dva broja postoji beskonačno mnogo drugih racionalnih brojeva. Dakle, takva mreža je "gusta" u R², i to je već problem drugog tipa. Uostalom, dokaz da je npr e iracionalan nije elementaran, a da nije ceo je dečja igra.

Razmisliću da li to zaista može jednostavnije.
Što se tiče tvoje nove rotacije, opet ispuštaš moju poentu: posle rotacije, temena poligona moraju biti u istom skupu tačaka, sa eventualno promenjenim rasporedom. Vrlo je prosto, ne razumem zašto ponavljaš primere koji ne odgovaraju onome o čemu pričam? A rotacija za ceo umnožak pravog ugla o kojoj sam ja pričao se odnosi na mrežu, koja je već kvadratna, tako da tu nema mnogo mudrosti.

Uostalom, evo formalno. Rotacija o kojoj ja pričam ima sledeću osobinu:
Neka je dat skup A temena poligona,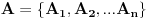
Rotacija 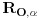je Darkova(c) rotacija akko je skup 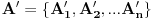temena rotiranog poligona, gde je 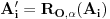, jednak skupu A, tj A' = A.
'El sad jasno?

Prvo, nisam ja navalio na racionalne brojeve, nego postavljač pitanja na cele, a ta dva problema su ekvivalentna. Naime, neka je A₁...A_n neki n-tougao sa temenima A_i(p_i/q_i, r_i/s_i) u racionalnoj rešetki. Ako je m bilo koji sadržalac svih brojeva q_i,s_i, onda njemu sličan poligon B₁...B_n sa temenima B_i(m*p_i/q_i, m*r_i/s_i) leži u celobrojnoj rešetki.

Drugo, napisao sam šta se dobija analizom rotacija koje prevode poligon u isti taj poligon (dakle, sa istim temenima) - da ne samo sinus, nego i kosinus spoljnog ugla pravilnog n-tougla mora biti racionalan broj. E, to je već potreban i dovoljan uslov da postoji traženi poligon. Dakle, ako na bilo koji način rešiš zadatak, ujedno ćeš dokazati da je n=4 jedini prirodan broj veći od dva takav da broj 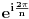ima algebarski stepen ne veći od dva nad poljem Q, to jest to će biti alternativan dokaz i te činjenice. E, to je već zadatak koji sam po sebi ima izvesnu težinu, tako da ako uspeš da nađeš neko njegovo alternativno rešenje, svaka ti čast. No, voleo bih prvo da vidim to rešenje.

Od sada pa nadalje, ne moraš me ubeđivati više da to može da prođe drugim metodama osim postovanja korektnog i jednostavnijeg rešenja.

a da li se važi ako nacrtam OGROMAN trougao? mislim, što je veći, to može biti približniji jednakostraničnom.

nisam siguran da li je neko već ovo pomenuo, nisam pročitao sve iznad

Pa ako uvedes novu definiciju : skoro jednakostranican :), pa onda i neku meru jednakostranicnosti :). E onda ces moci da za zadatu toleranciju moci da nadjes vejikiiiiiiii trokut kod kojeg je mera jednakostranicanosti manja od te tolerancije :).

Ali da nactras bas bas bas jednakostranican ne mere (kao i sto dokazali ljudi :) ).

Uostalom 2+2 = 5 za dovoljno velike vrednosti 2