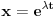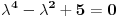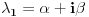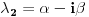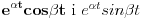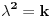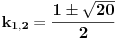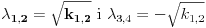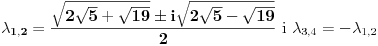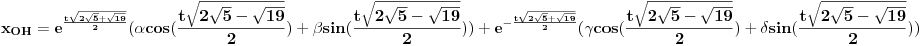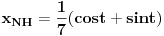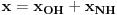[ BlackSnake @ 17.02.2005. 14:48 ] @
| Dakle, diferencijalna j-na glasi: X^4 - X^2 + 5X = sin t + cos t Riješiti je primjenom Laplasove transformacije. Kako da prevedem lijevu stranu. Da li je ovo ^4 četvrti izvod? Ako jeste onda kada prevedem lijevu stranu dobijam četverostepeni izraz u imeniocu koji mi pravi probleme kada ga hoću vratiti inverznom transformacijom. Napominjem da nisam ekspert pa bi molio za neku uputu kada mi se sa lijeve strane nađe potencija veća od ^2 , jer onda se komplikuje razlaganje imenioca. Nadam se da sam bio jasan. Hvala unaprijed. |