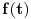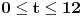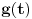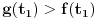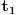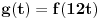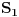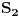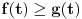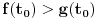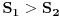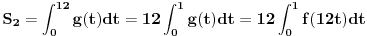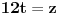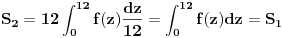[ Bojan Basic @ 18.02.2005. 14:41 ] @
|
| Evo jednog vrlo lepog zadatka - ako ne možete da ga rešite napišite makar svoj tok razmišljanja, ideje, predloge, itd. Ako ne bude interesovanja ili napretka objaviću rešenje za oko 2 nedelje.
Nekoliko satova se nalazi na stolu. Poznato je da postoji momenat u kom zbir rastojanja od proizvoljne tačke X na stolu do vrhova minutnih kazaljki nije jednak zbiru rastojanja od tačke X do vrhova satnih kazaljki. Dokazati da postoji momenat u kom je zbir rastojanja od tačke X do vrhova minutnih kazaljki veći od zbira rastojanja od tačke X do vrhova satnih kazaljki.
P. S. Nije navedeno u originalnoj postavci zadatka, ali neophodno je dodati i ovaj uslov: pretpostaviti da minutna i satna kazaljka svakog pojedinačnog sata imaju istu dužinu (što naravno ne mora da znači da su sve kazaljke iste dužine). |
[ gpreda @ 18.02.2005. 15:40 ] @
Ovo bi trebalo da bude dokaz, ali posto sam izostavio dosta detalja moze da se shvati i kao ideja:
Neka je t vremenski trenutak u periodu od 12 sati (dovoljno je posmatrati samo 12 sati jer posle se sve ponavlja). Posmatrajmo samo jedan sat.
Neka je f(t) razdaljina od tacke posmatranja do vrha satne kazaljke u trenutku t, i g(t) slicno za minutnu kazaljku.
Moze se dokazati da je:
(L1) integral (0, 12) f(t) dt = integral (0, 12) g(t) dt
Sada se vratimo na sve casovnike, neka ih ima ukupno n. Definisimo funkcije:
F(i, t) = f(t) za i-ti casovnik
G(i, t) = g(t) za i-ti casovnik
F(t) = suma (1, n) F(i, t)
G(t) = suma (1, n) G(i, t)
Zadatak je u stvari da se dokaze da postoji t za koje je G(t) > F(t) (ili obrnuto, ali nema veze to je isto).
Iz (L1) direktno sledi:
(L2) integral (0, 12) F(t) dt = integral (0, 12) G(t) dt
Sada je jasno da ne moze vaziti da je (za svako t) F(t) <= G(t) (negacija tvrdjenja zadatka), jer bi u tom slucaju bilo i:
integral (0, 12) F(t) dt >= integral (0, 12) G(t) dt
(*) gde je znak jednakosti samo u slucaju da je (za svako t) F(t) = G(t).
Uz uslov iz zadatka da postoji trenutak kada je F(t) razlicito od G(t), ovo je jasna kontradikcija.
Jedini problematican deo je (*), to se moze dokazati koristeci cinjenice da su F i G neprekidne i diferencijabilne funkcije.
[ pirgos_madden @ 18.02.2005. 15:52 ] @
Imam pitanje. Da li casovnici u svakom trenutku pokazuju isto vreme - nisam nesto previse razmisljao ali eto ovo mi je palo,..., mozda je bitno? Jos nesto, pretpostavljam da, obzirom da si rekao da je zadatak "vrlo lep", zadatak moze da se resi krajnje elementarno ?
[ Bojan Basic @ 18.02.2005. 16:05 ] @
Citat:
pirgos_madden:
Imam pitanje. Da li casovnici u svakom trenutku pokazuju isto vreme - nisam nesto previse razmisljao ali eto ovo mi je palo,..., mozda je bitno?
Svi časovnici pokazuju tačno vreme.
Citat:
pirgos_madden:
Jos nesto, pretpostavljam da, obzirom da si rekao da je zadatak "vrlo lep", zadatak moze da se resi krajnje elementarno ?
Rekao sam da je zadatak vrlo lep zato što se, iako nije preterano težak, na osnovu postavke zaista ne očekuje da će u rešenju isplivati određeni integral — zvanično rešenje koje ja imam (zadatak je bio na 52. Beloruskoj matematičkoj olimpijadi) vrlo je slično ovome koje je napisao gpreda, kasnije ću napisati malo detaljnije i preglednije. Da li može elementarno, to ne znam, ali probaj pa ako uspeš javi.
@gpreda:
Sve čestitke za rešenje, zaista nisam očekivao ovako brz odgovor.
[Ovu poruku je menjao Bojan Basic dana 04.04.2009. u 21:58 GMT+1][ Bojan Basic @ 09.03.2005. 15:41 ] @
Evo, zvaničnog rešenja, to je zapravo to što je gpreda napisao samo malo preglednije:
Neka je
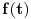
zbir rastojanja od tačke

do vrhova svih satnih kazaljki u trenutku

,
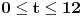
, gde je

vreme mereno u satima. Slično, neka je
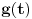
zbir rastojanja od tačke

do vrhova minutnih kazaljki u trenutku

. Treba dokazati da je
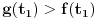
za neko
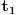
.
Očigledno je da je
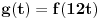
. Osim toga,
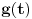
je periodična funkcija sa periodom

. I

i

su neprekidne. Neka su
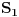
i
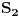
površine ispod grafika

i

, redom, za
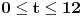
. Pretpostavimo suprotno: neka je
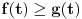
za svako
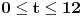
. Pošto je
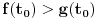
imamo da je
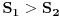
. S druge strane, važi da je:
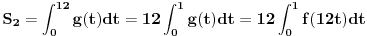
Ako uvedemo smenu
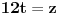
, dalje imamo:
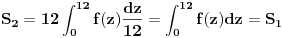
.
Kontradikcija.
Morate priznati, zaista lepo rešenje. Ako neko zna neki elementarniji pristup ili ima neko pitanje/komentar slobodno neka napiše.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.