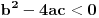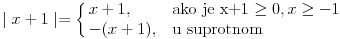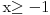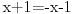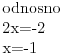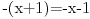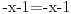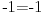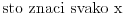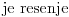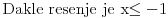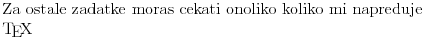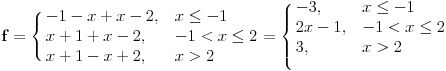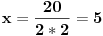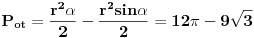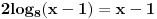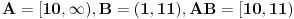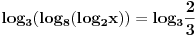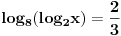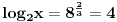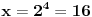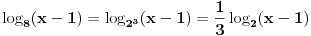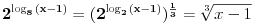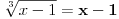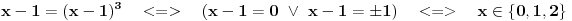[ maximus_1 @ 22.02.2005. 19:11 ] @
| Ovako, imam par zadataka koje ne znam riješiti pa ako netko zna bar jedan neka mi napiše kako to treba učiniti... Hvala unaprijed ______________________________________________________________________ 1. Skup rješenja jednadžbe |x+1|=-x-i je... 2. Najmanji cijeli broj m takav da funkcija y=(m-2)x2+m+2+3x ima pozitivne vrijednosti na cijeloj domeni 3. Najveća vrijednost funkcije f(x)= |1+x|-|x-2| je... 4. Za koju točku na osi x vrijedi da joj je suma kvadrata udaljenosti od točaka A(2,4) i B(8,2) najmanja? 5. Polumjer kružnice iznosi 6 cm. Površina odsječka kojemu je pripadni središnji kut 2π/3 je ... 6. Rješenje jednadžbe 2log8(x-1)=x-1 je u intervalu... 7. Jednadžba parabole kojoj je os paralelna osi x i prolazi točkama A(-1,2), B(5,6), C(5,-10) je... 8. Središte kružnice je na pravcu x-2y + 2=0, a pravac 3x+y-2=0 je dira u točki T(0,2). Jednadžba te kružnice je... 9.Presjek skupova A = {x € R:logx >= 1} i B = {x € R:│x-6│<5} je ... 10. log3log8log2(x+9)= -1 + log32 11. Vrijednost realnog parametra a takvog da polinomi p(x)=x3+ ax + b i q(x)= x2+1 budu djeljivi je... |