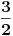[ Metalnem @ 24.02.2005. 15:53 ] @
|
[ Srđan Krstić @ 24.02.2005. 18:48 ] @
Bio je na nekom bas starom shortlistu, mozda cak i izabran za IMO, toga se vec ne secam. Sad nesto nemam vremena, ali cini mi se da moze da prodje Muirhead kad se izmnozi. Naravno, ima i neko bas lepo resenje, ali Muirhead je zakon ;). Aj cu probam malo kasnije da odradim pa cu da se javim.
[ Bojan Basic @ 24.02.2005. 19:43 ] @
Verovatno postoji i neko rešenje u kojem se koristi manje snažan aparat (ovo što ćeš sad videti ti dođe otprilike kao gađanje muve topovskim đuletom) ali zašto ne koristiti ono što nam matematika pruža, pogotovo ako na prvi pogled znaš da ova metoda ne može da omane kod sličnih zadataka. Da ne dužim priču, rešenje ide ovako:
Neka je 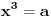 , , 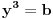 , , 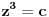 . Očigledno je da važi . Očigledno je da važi 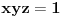 . Na osnovu Mjurhedove nejednakosti (imaš negde na ES-u temu o njoj, ako ti nešto oko same nejednakosti ne bude jasno zamolio bih te da pitaš na toj temi a ne ovde, da ne bi došlo do mešanja diskusija) imamo: . Na osnovu Mjurhedove nejednakosti (imaš negde na ES-u temu o njoj, ako ti nešto oko same nejednakosti ne bude jasno zamolio bih te da pitaš na toj temi a ne ovde, da ne bi došlo do mešanja diskusija) imamo: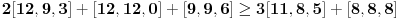 (da ne objašnjavam sad šta predstavljaju ove uglaste zagrade, shvatićeš to kad naučiš Mjurhedovu teoremu). (da ne objašnjavam sad šta predstavljaju ove uglaste zagrade, shvatićeš to kad naučiš Mjurhedovu teoremu).Razlaganjem ovoga dobijamo: 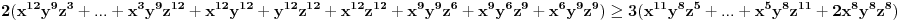 Sad koristimo činjenicu da je 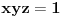 i ovo svodimo na sledeće: i ovo svodimo na sledeće: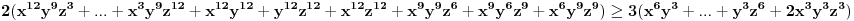 Jednostavno vratimo početna slova i dobijamo: 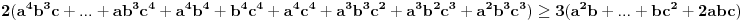 Faktorizacijom ovih izraza dobijamo sledeće (usput možemo desnu stranu pomnožiti sa 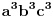 ): ):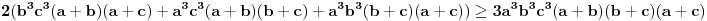 I za kraj, podelimo sve sa 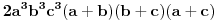 , što nas vodi do , što nas vodi do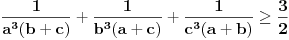 što je i trebalo dokazati. [ Metalnem @ 26.02.2005. 11:09 ] @
Nasao sam jos jedan nacin. Neka je
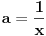 , , 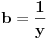 i i 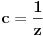 . Zamenom u levu stranu polazne nejednakosti dobijamo . Zamenom u levu stranu polazne nejednakosti dobijamo 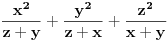 (koristili smo to da je xyz takodje 1). Za ovaj izraz treba dokazati da je veci od (koristili smo to da je xyz takodje 1). Za ovaj izraz treba dokazati da je veci od 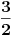 . Preko Kosijeve nejednakosti dobijamo da je . Preko Kosijeve nejednakosti dobijamo da je 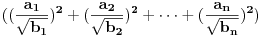 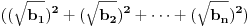 ≥ ≥ 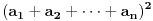 to jest, to jest, 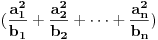 ≥ ≥ 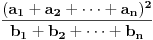 . Primenjujuci to na . Primenjujuci to na 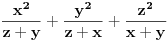 dobijamo dobijamo 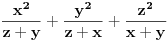 ≥ ≥ 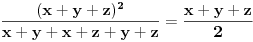 . Primenjujuci nejednakost aritmeticke i gometrijske sredine dobijamo da je . Primenjujuci nejednakost aritmeticke i gometrijske sredine dobijamo da je 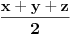 vece ili jednako od vece ili jednako od 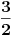 cime je dokaz zavrsen. cime je dokaz zavrsen.[ Nedeljko @ 26.02.2005. 18:16 ] @
Sram te bilo, ne samo da si našao elementarniji dokaz tražene nejednakosti, nego si je čak i uopštio na proizvoljan broj sabiraka. Štaviše, ako se izbaci poslednji korak sa primenom AG nejednakosti, uz neznatne prepravke se dobija strožija nejednakost. SVAKA ČAST! Inače, za sve ljubitelje ovakve problematike imam ovaj dobar link
http://my.netian.com/~ideahitme/eng.html [ Metalnem @ 28.02.2005. 20:40 ] @
Hvala ti za link, stvarno je izuzetan.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|